一、堆的定义
首先明确堆是一种特殊的完全二叉树，分为大根堆和小根堆，接下来我们就分别介绍一下这两种不同的堆。
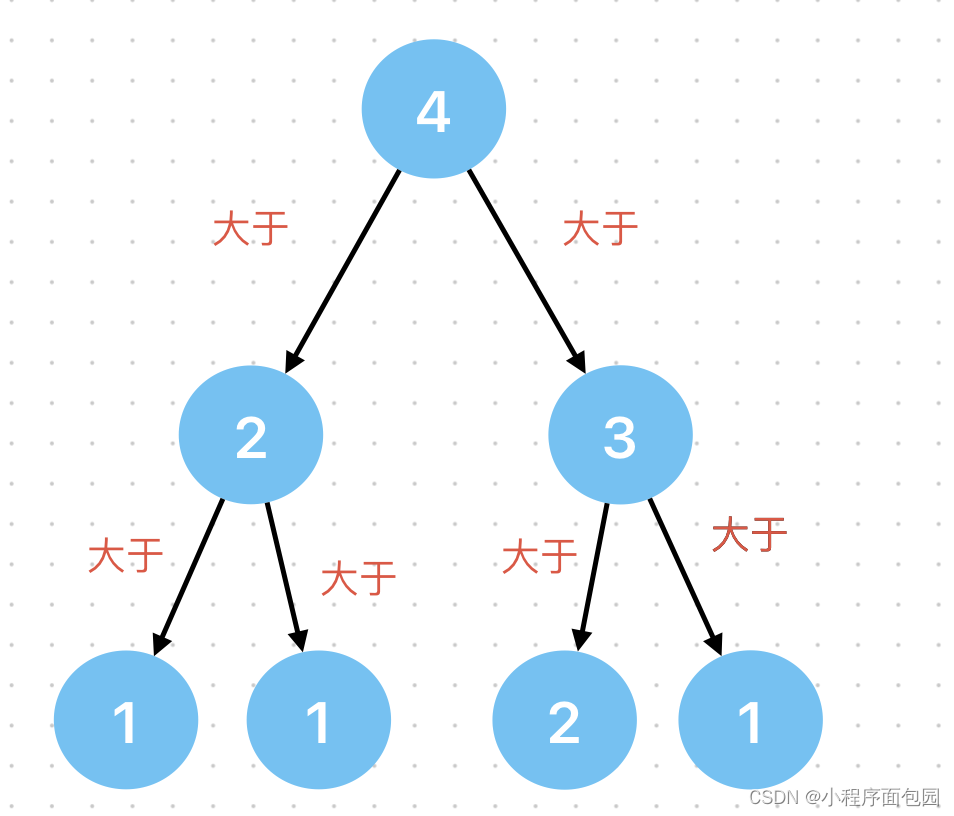
1.1 大根堆（简称：大堆）
在大堆里面：父节点的值 ≥ 孩子节点的值
我们的兄弟节点没有限制，只要保证每个父节点都≥孩子节点就行。
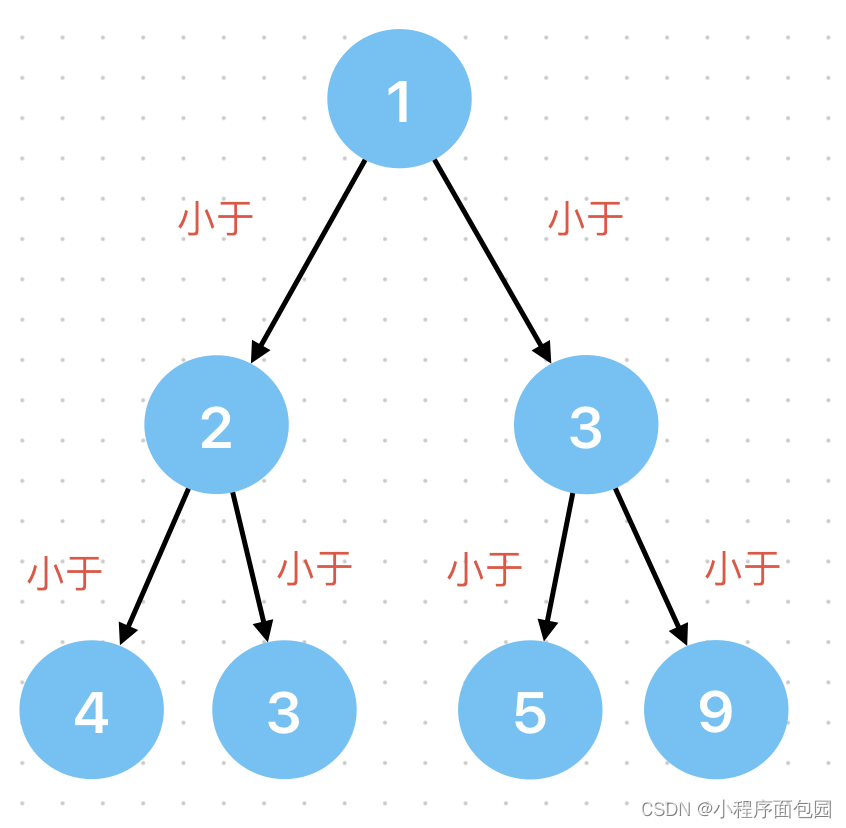
1.2 小根堆（简称：小堆）
在小堆里面：父节点的值 ≤ 孩子节点的值
同样兄弟节点也没有限制，只要保证每个父节点都≤孩子节点就行。
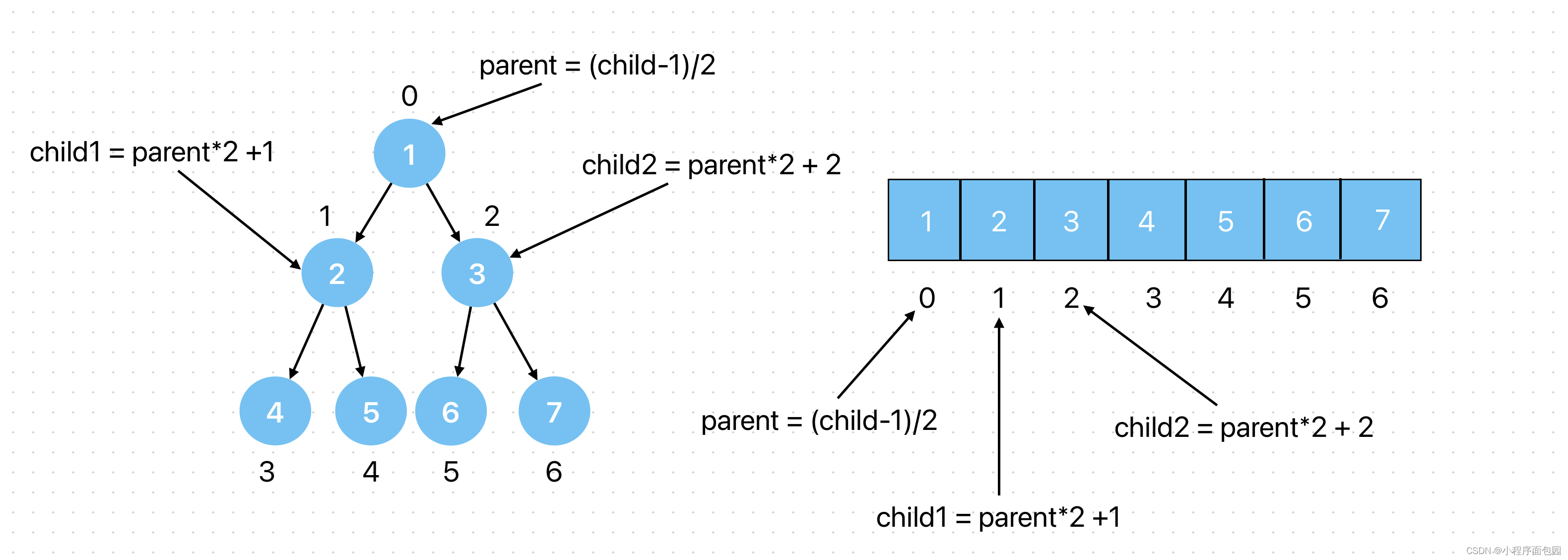
这里就又用到了我们的父节点和孩子节点的位置关系了，我们可以用顺序结构来模拟完全二叉树，也就是数组来实现，话不多说，直接给公式和图形：
parent = （child-1)/2; (任意一个child节点)
child1 = parent*2 + 1;
child2 = parent*2 + 2;
这里是运用数组下标进行计算
二、堆的实现
我们形成堆有两种方法，一种是向下调整，一种是向上调整，在未来，经常会用到向下调整，所以我们只介绍这种方法。
2.1 向下调整法
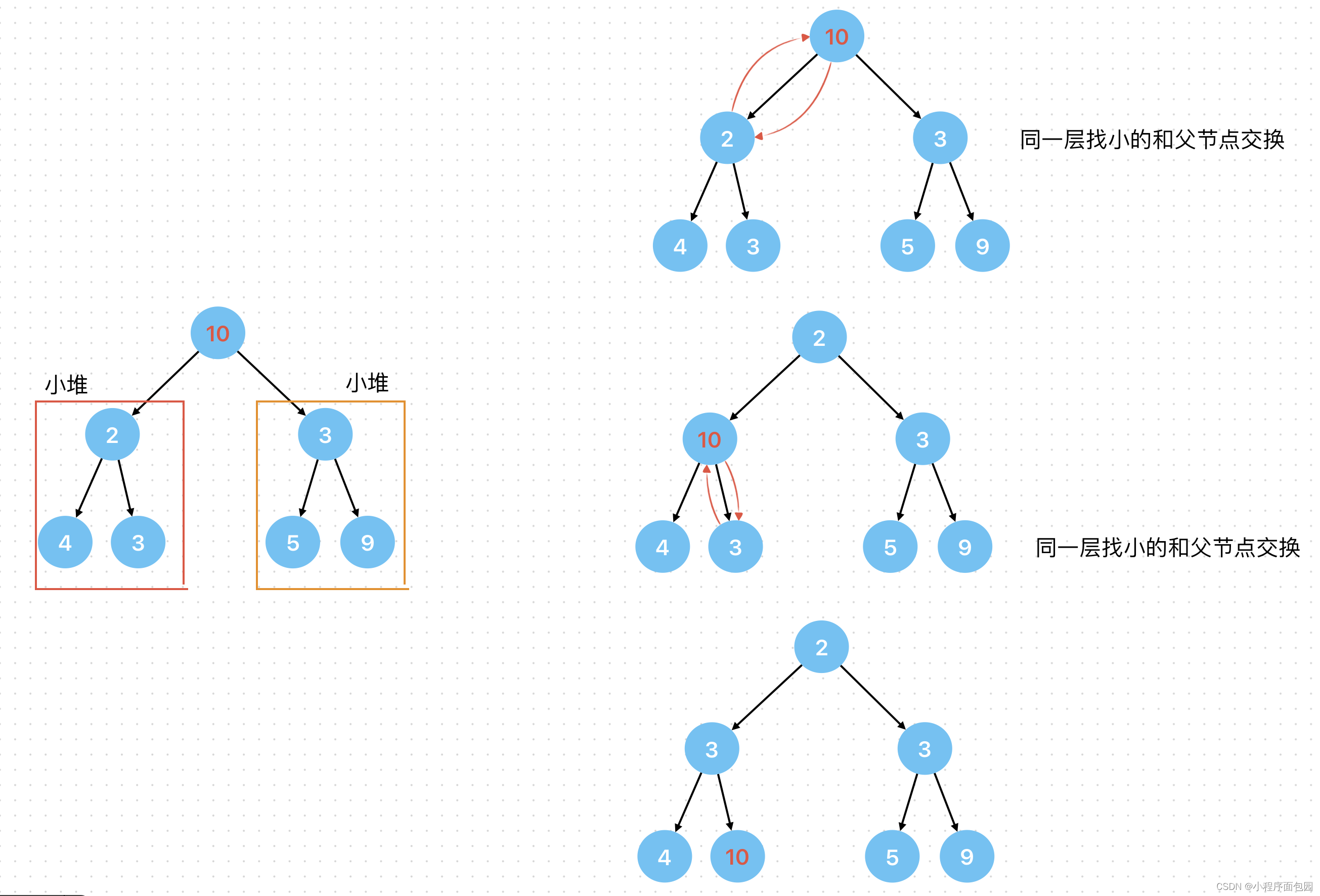
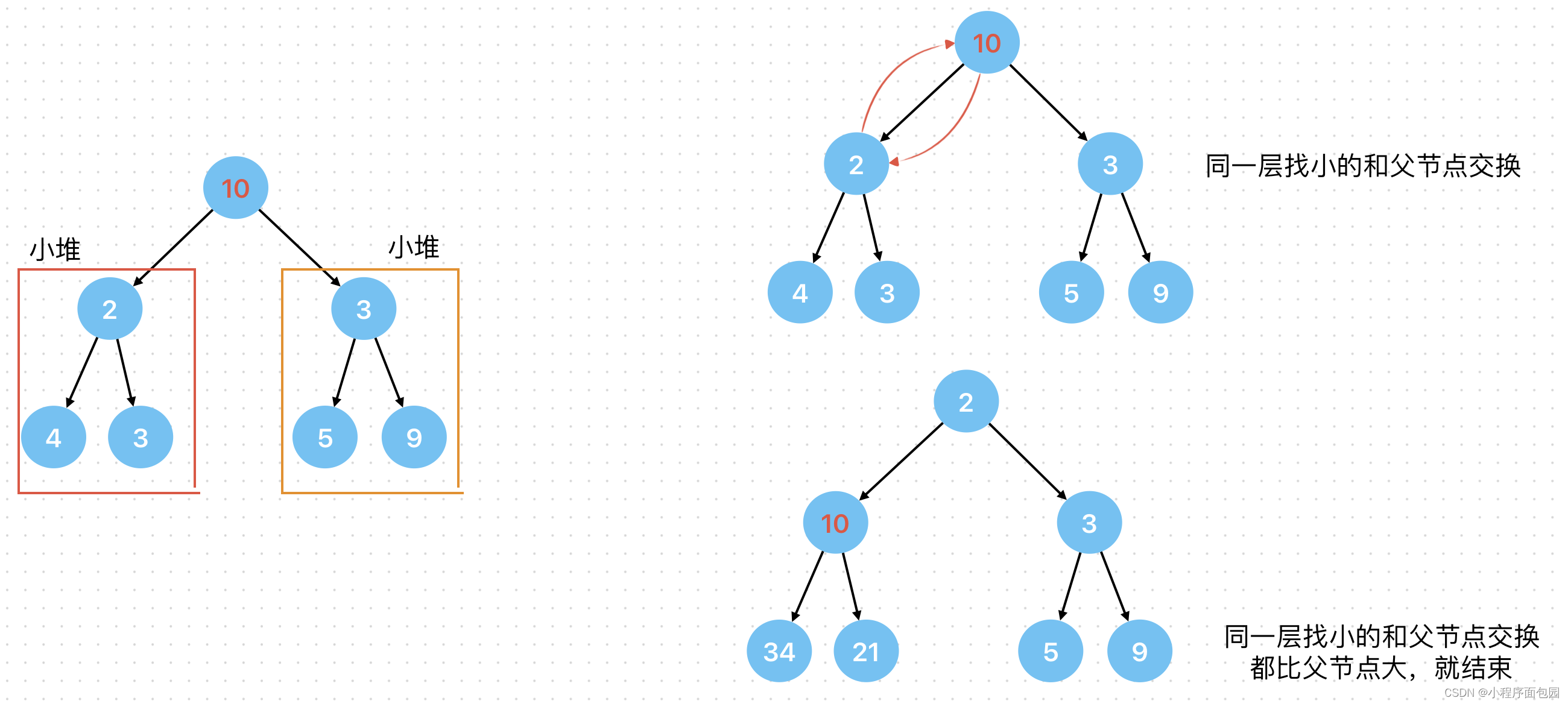
什么是向下调整呢？就是把我们的完全二叉树从从上往下建堆，使用向下调整法的前提就是根的左右子树必须是堆。
首先我们要建小堆，先找到同一层的小的那个和父节点交换，以此类推，直到10到叶节点或者没有比他小的。
2.2 堆的定义
在这里我们的堆的存储结构都是数组，所以在定义的时候跟定义顺序表一样，只不过在插入删除上有区别
typedef struct Heap
{int* arr; int capacity; //数组的容量int size; //有效的元素个数
}Heap;2.3 堆的初始化
//堆的初始化
void HeapInit(Heap* php)
{assert(php);php->arr = NULL;php->capacity = 0;php->size = 0;
}2.4 堆的创建
//堆的创建
void HeapCreate(Heap* php)
{assert(php);if(php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : (php->capacity)*2;int* data = (int*) realloc(php->arr,sizeof (int)*newCapacity);if(data == NULL){perror("malloc fail");exit(-1);}php->arr = data;php->capacity = newCapacity;}
}2.5 堆的销毁
//堆的销毁
void HeapDestroy(Heap* php)
{assert(php);free(php->arr);php->arr = NULL;php->size = 0;php->capacity = 0;
}2.6 堆的插入
在插入这里我们就要建堆了，但是由于我们的数据是顺序插入的，所以没有办法进行向下调整，这里使用向上调整的方法，原理都是一样的，向上调整就要保证插入的节点以上是堆。
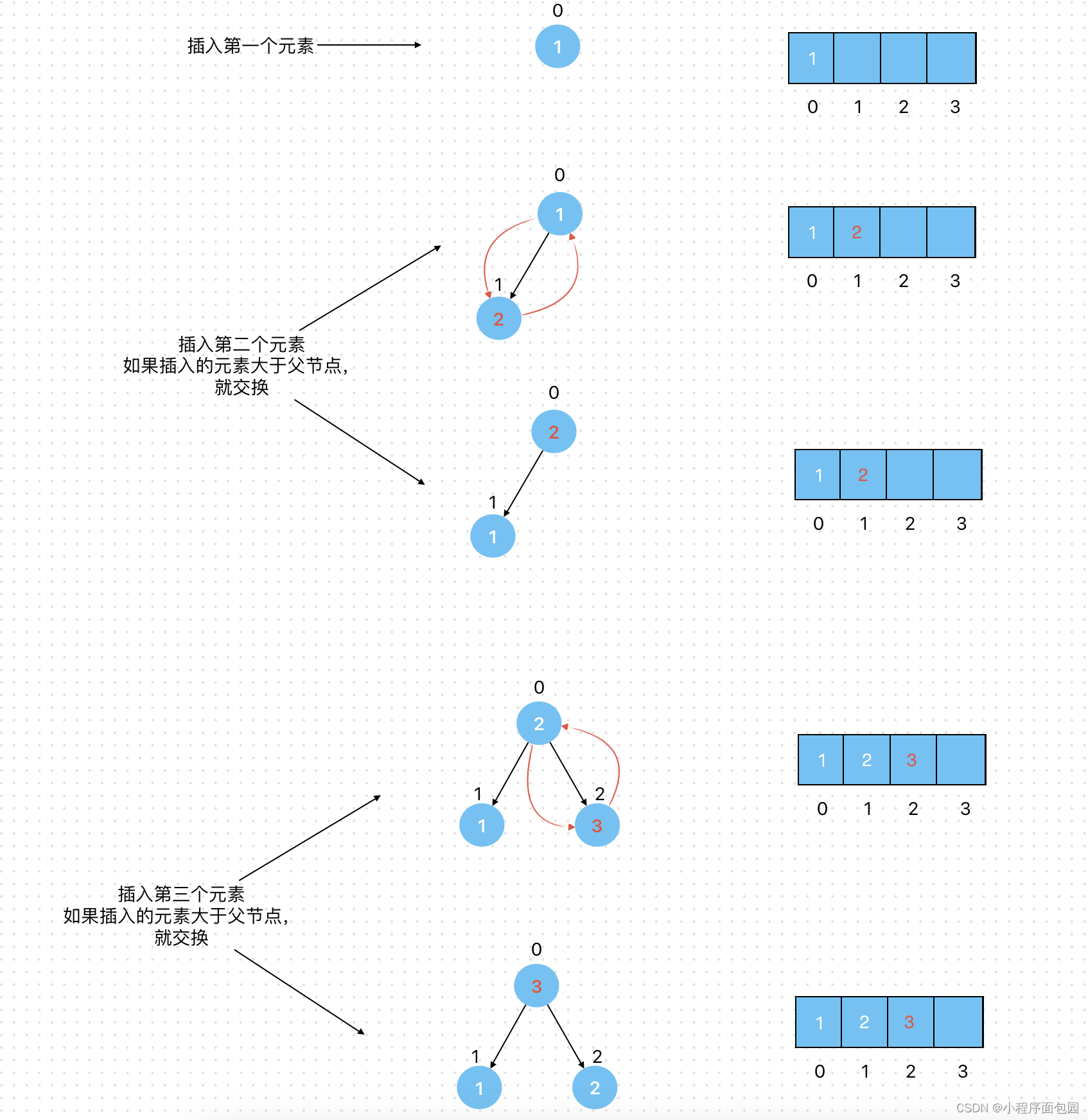
void Swap(int* x,int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//建立大堆,向上调整
void AdjustUp(int* arr,int child)
{int parent = (child-1)/2;while (child > 0){if(arr[child] > arr[parent]){Swap(&arr[child],&arr[parent]);child = parent;parent = (child-1)/2;}elsebreak;}
}
//堆的插入
void HeapPush(Heap* php,int x)
{HeapCreate(php);php->arr[php->size] = x;php->size++;//建立大堆AdjustUp(php->arr,php->size-1);
}
2.7 删除根节点
void Swap(int* x,int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//建立大堆，向下调整
void AdjustDown(int*arr,int parent,int size)
{int child = parent*2 + 1;while (child < size){if(child + 1 < size && arr[child] > arr[child+1]){child = child + 1;}if(arr[child] < arr[parent]){Swap(&arr[child],&arr[parent]);parent = child;child = parent*2 + 1;}elsebreak;}
}
//堆的删除
void HeapPop(Heap* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->arr[0],&php->arr[php->size-1]);php->size--;AdjustDown(php->arr,0,php->size);
}2.8 取堆顶的数据
//堆的根节点
int HeapTop(Heap* php)
{assert(php);assert(!HeapEmpty(php));return php->arr[0];
}2.9 判断堆是否为空
//判断堆是否为空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}2.10 堆的数据个数
//堆的节点个数
int HeapSize(Heap* php)
{assert(php);return php->size;
}
