- 语音识别的Jtrain、Jcv和人工误差

- 对于逻辑回归问题,Jtrain和Jcv可以用分类错误的比例,这一方式来代替
- 单单只看Jtrain,不好区分是否高偏差。可以再计算人类识别误差,即人工误差,作为基准线来进行比较
- Jtrain与baseline对比只高了0.2%,所以不算高偏差,但Jcv与Jtrain对比高了4.0%,这算高方差
- baseline的选取

- 基准线baseline,即期望学习算法最终达到的合理误差水平
- 当期望误差baseline不为0时,我们可以选用人工性能、其他算法性能或相关以往经验作为baseline,并进行相对的比较
- 如何通过baseline、Jtrain和Jcv区分高偏差和高方差

- 通过比较baseline和Jtrain来判断是否为高偏差,若认为此处的0.2%很大,则为高偏差
- 通过比较Jtrain和Jcv来判断是否为高方差,若认为此处的4%很大,则为高方差
- 一般通过比较baseline和Jtrain、Jtrain和Jcv之间的差值,相对的来判断是否为高偏差和高方差
- 学习曲线

- 二阶多项式/二次函数的学习曲线如图,x轴为训练集大小,y轴为误差,即Jtrain或Jcv
- 当训练集很小只有一两个实例时,只需一条直线即可拟合训练集,但此时为过拟合,若出现一个新实例则极大可能拟合失败。所以训练集很小时,Jtrain很低,但Jcv很高
- 当训练集再大一些时,用二次函数可能很难拟合全部数据,但若出现一个新实例则大概率拟合成功。所以训练集越来越大时,Jtrain逐渐增大,Jcv逐渐降低
- 通常,Jcv会高于Jtrain,因为我们是对训练集拟合的模型,所以会更适合训练集,而不是验证集
- 综上:训练集越大越难训练/拟合,但也越容易推广/泛化。
- 高偏差的学习曲线图

- 一阶多项式/一次函数的高偏差的学习曲线如图,高偏差表示Jtrain很高,且Jtrain近似于Jcv。
- 当训练集很小时,模型能拟合全部数据,但对新数据的泛化能力很差,所以一开始Jtrain很小,同时Jcv很大。
- 当训练集开始增大时,模型开始出现对训练集拟合错误,同时也会更适应验证集,所以Jtrain增大而Jcv减小,但由于此时为欠拟合,所以Jtrain和Jcv均高于baseline
- 但由于一阶多项式模型太简单且能拟合的数据太少,所以即便训练集越来越大,模型依旧无法做出太大的改变,仍然只能拟合一小部分数据。而Jtrain和Jcv都是计算的平均误差,既然模型基本不改变,那么就算实例越密集(即训练集越来越大),平均误差也基本基本不变。所以Jtrain和Jcv最终逐渐靠近并趋于平坦,但始终保持Jcv高于Jtrain,且均高于baseline
- 综上:如果一个算法有高偏差,那么增加训练集大小并不能显著降低Jcv误差
- 高方差的学习曲线图
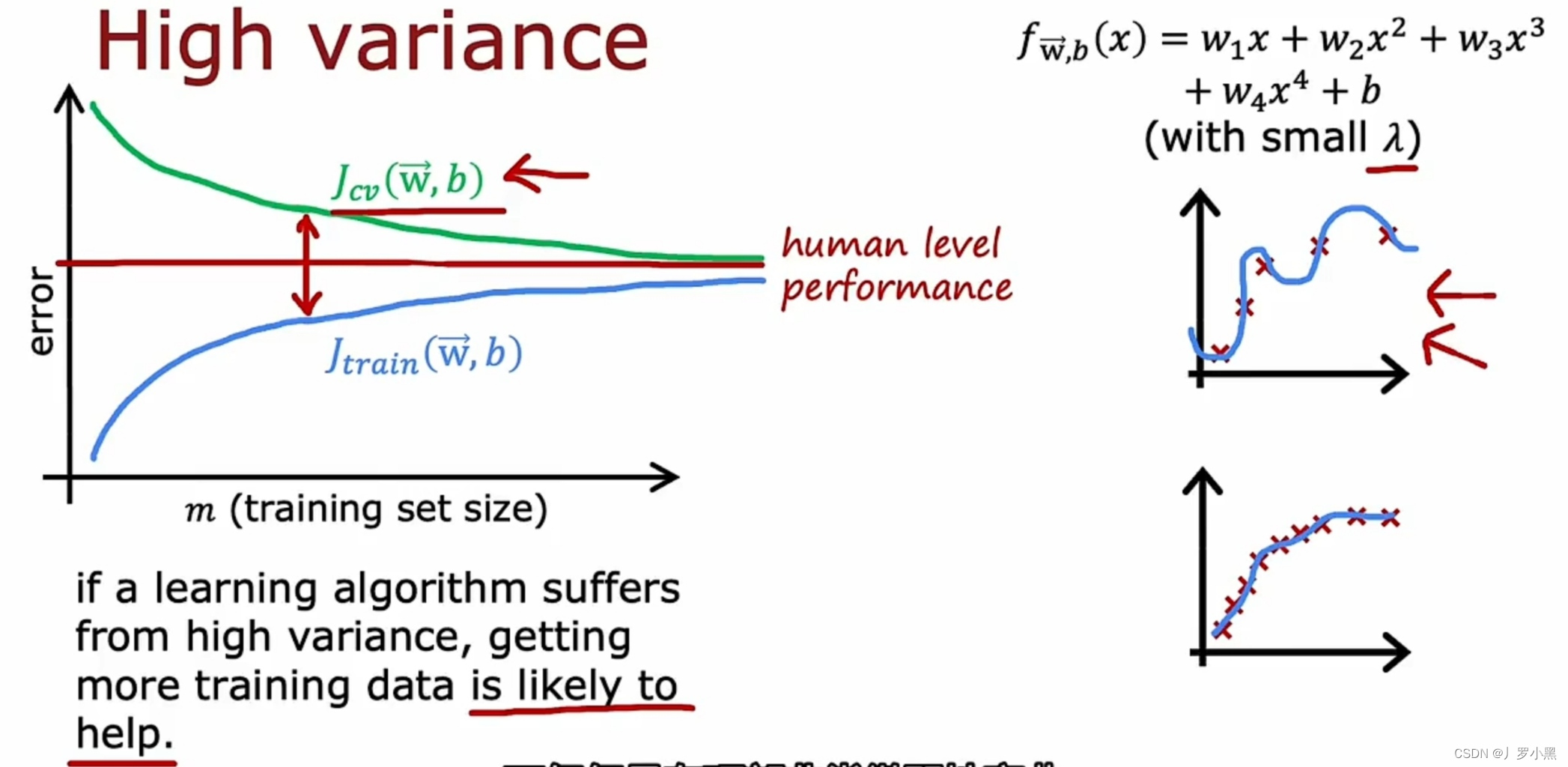
- 一个四阶多项式,且λ取较小值的高方差的学习曲线如图,高方差表示Jcv远大于Jtrain,且Jtrain很小,随着训练集越来越来大,Jtrain和Jcv逐渐靠近baseline
- 当训练集较小时,模型能拟合全部数据,但对新数据的泛化能力很差,所以一开始,Jtrain很小而Jcv很大
- 当训练集开始增大时,模型开始出现对训练集拟合错误,但由于此时为过拟合,所以Jtrain仍比baseline要低,而Jcv远大于Jtrain,所以Jcv要比baseline高
- 由于四阶多项式比较复杂且能拟合较多数据,所以当训练集很小时,Jtrain比期望的baseline要小很多,但该模型对新数据的泛化能力很弱,所以Jcv要比baseline高很多。随着训练集越来越来大,模型会稍稍增大Jtrain的值,以便Jcv迅速下降,最终达到Jtrain和Jcv都逐渐逼近baseline的效果
- 如果一个算法有高方差,那么增加训练集大小可以显著降低Jcv误差



)






)

第32篇:我当高校教师的这几年 VIII)






