手把手教你从0入门线段树~

1. 什么是线段树?

1.1 初探线段树

定义：线段树是一种用于解决区间查询问题的数据结构，是一种广义上的二叉搜索树。

原理：它将一个区间划分为多个较小的子区间，并为每个子区间存储一些有用的信息，例如最大值、最小值或总和。

可以解决的问题：通过将区间存储的信息逐级向上汇总，线段树可以快速回答各种类型的区间查询，例如求和、最大值、最小值或更新某个区间的值。

**时间复杂度：**线段树的构建和查询操作的时间复杂度都是O(logN)，其中 N 是区间的大小。

限制条件：能用线段树解决的问题必须满足区间加法，区间加法也就是对于[L,R] 区间，它的答案可以由[L,M] 和 [M+1,R] 的答案合并给出。其中，M 是区间的中点。

1.2 线段树与二叉树的区别

对于一个数组 [1,2,3,4,5,6]，它的二叉树和线段树如下图所示**「区间下标从 0 开始」**：

从图中可以看出，二叉树中单个节点存储的内容是值 val，而线段树中存储的是区间信息。

观察线段树，我们还可以快速得出以下结论：

  • 每个节点的左右孩子，分别存储该节点区间的一半
  • 当区间无法划分时，得到叶子节点

1.3 线段树的下标

接着，我们给线段树的每个节点加上数组的下标，得到的结果如下：

可以看到，在线段树中，当节点的下标为 i 时，其左孩子的下标为 2 * i + 1，右孩子的下标为 2 * i + 2。这个时候，我们需要考虑一个问题：当数组大小是 n 时，线段树的空间应该为多少?

答案：2 * n - 1，在一颗完全二叉树中，叶子节点的数量等于非叶子结点的数量减一。在线段树中，叶子节点的个数等于数组大小 n ，非叶子节点的个数为 n - 1，因此线段树的空间应该为 2 * n - 1。注意，为了方便计算以及防止数组越界，我们通常会将线段树的空间大小开到比总节点数更大的最小的2的幂次方，即 4*n 大小的空间。

1.4 线段树的存储内容

1.1 小节中说到：线段树可以快速回答各种类型的区间查询，例如求和、最大值、最小值。那么在求和中，线段树是如何表示的呢？

可以看到，每个叶子节点的存储的是数组下标值 val，每个非叶子节点的求和值等于其左右孩子节点存储值之和；同理，在最大\最小值中，非叶子节点存储的值是其左右孩子节点中的较大\较小值。

2. 线段树解决问题的步骤

2.1 建树

虽然线段树中存储的是一段区间的信息，但我们并不需要定义一个类，让它存储区间左值，区间右值以及求和。因为我们可以借助递归+下标关系的方式创建线段树，这样线段树的节点就只需要存储求和。

int nums[] = new int[]{1, 2, 3, 4, 5, 6};
int n = nums.length;
int[] segTree = new int[4 * n]; // 为线段树分配空间void buildTree(int index, int left, int right) { // index 表示下标，left 表示左区间，right 表示右区间if (left == right) {segTree[index] = nums[left];return; // 到叶子节点就不能继续划分啦~}int mid = (left + right) / 2; // 一分为 2，例如将 [1,6] 划分为 [1,3] 和 [4,6]buildTree(2 * index + 1, left, mid); // 构建左子树，左孩子的下标为 2 * index + 1buildTree(2 * index + 2, mid + 1, right); // 构建右子树，右孩子的下标为 2 * index + 2segTree[index] = segTree[2 * index + 1] + segTree[2 * index + 2]; // 这里是求和，所以非叶子节点存储的值是左右孩子节点存储的值之和
}public static void main(String[] args) {Solution solution = new Solution();solution.buildTree(0, 0, solution.nums.length - 1);}

2.2 单点修改

单点修改是区间修改的一种特殊情况，我们先从简单的单点修改看看线段树是如何实现更新的。

思路：假如我们要更新数组的第 i 个值为 x ，那么我们可以从根节点去寻找区间左侧和区间右侧均等于 i 的节点，修改它的值。然后在返回的路上不断更新其祖先节点的值。

public void update(int i, int value) {update(0, 0, nums.length - 1, i, value);
}private void update(int index, int left, int right, int i, int value) { // i 表示要更新数组的下标，value 是更改后的值if (left == right) { // 当搜寻到叶子节点的时候，就可以修改了，前提是 i 在[0,2 * n - 2] 之间，下标从 0 开始算segTree[left] = value;return; // 赋值完就结束}int mid = (left + right) / 2;if (i <= mid) update(2 * index + 1, left, mid, i, value);else update(2 * index + 2, mid + 1, right, i, value);segTree[index] = segTree[index * 2 + 1] + segTree[index * 2 + 2]; // 更新祖先节点
}

2.3 仅存在单点修改的区间查询

还记得线段树的使用条件吗？必须满足区间加法

因此，当我们查询一个区间 [a,b] 时，可以将其拆分成满足区间加法的子区间。还是以求和为例：sum[1,5] = sum[1,3] + sum[4,5]，sum[2,5] = sum[2,2] + sum[3,3] + sum[4,5] 。

public int query(int x, int y) {return query(0, 0, nums.length - 1, x, y);}private int query(int index, int left, int right, int x, int y) { // x 表示要查询的左区间，y 表示要查询的右区间if (x > right || y < left) return 0; // 如果查询区间在线段树区间外返回 0 if (x <= left && y >= right) return segTree[index];  // 当查询区间包含线段树区间，返回节点值int mid = (left + right) / 2;int leftQuery = query(2 * index + 1, left, mid, x, y); // 计算左孩子int rightQuery = query(2 * index + 2, mid + 1, right, x, y); // 计算右孩子return leftQuery + rightQuery; // 求和 }

2.4 区间修改

当我们需要修改的内容是一个区间而不是一个单点，就不能通过 for 循环的方式调用单点循环，因为这样与暴力破解无异。

为了解决这个问题，我们需要引入一个新的概念：延迟标记，你也可以叫它懒标记。这个标记的意义是：被这个标记过的区间值已经被更新，但它的子区间未被更新，更新的信息是标记中存储的值。

引入延迟标记的区间修改遵循以下规则：

（1）如果要修改的区间完全覆盖当前区间，直接更新这个区间，并打上延迟标记

（2）如果没有完全覆盖，且当前区间有延迟标记，先下传延迟标记到子区间，再清除当前区间的延迟标记。

（3）如果修改区间与左儿子有交集，就搜索左儿子；如果与右儿子有交集，就搜索右儿子

（4）更新当前区间的值

文字太多，是不是感觉头晕了。没关系，我们用一个具体的例子来看看区间修改~

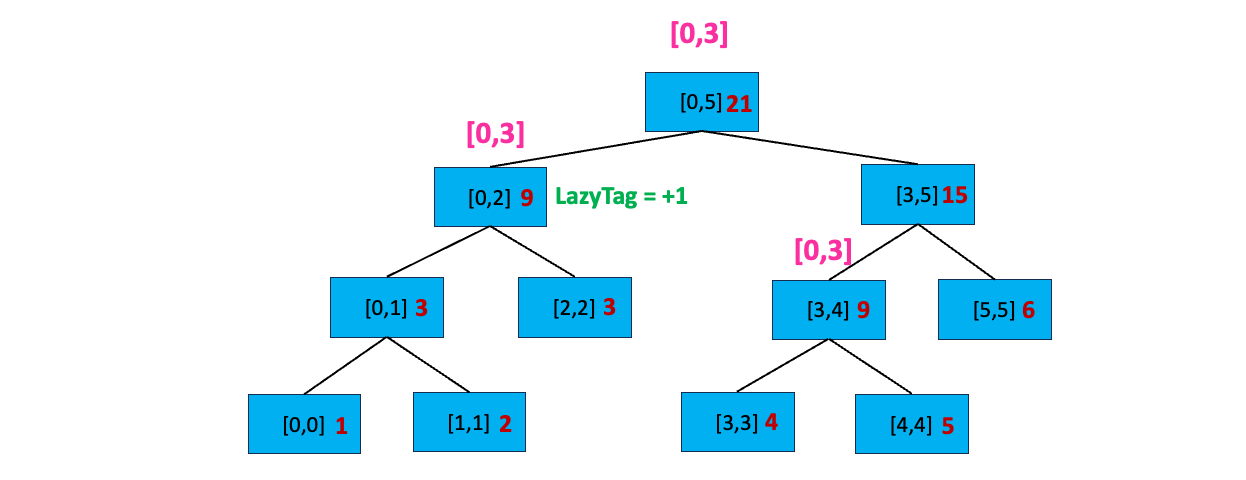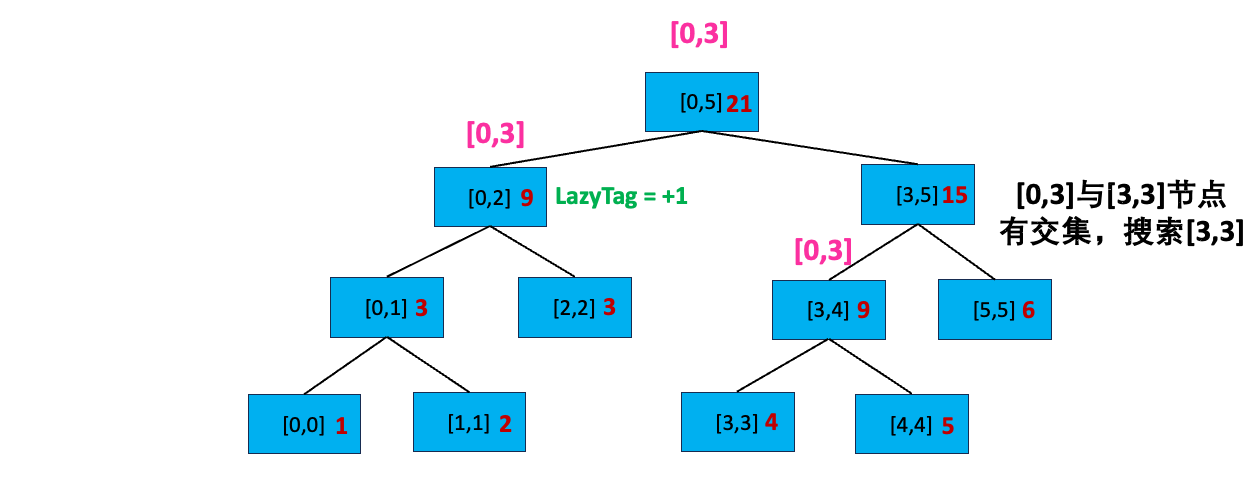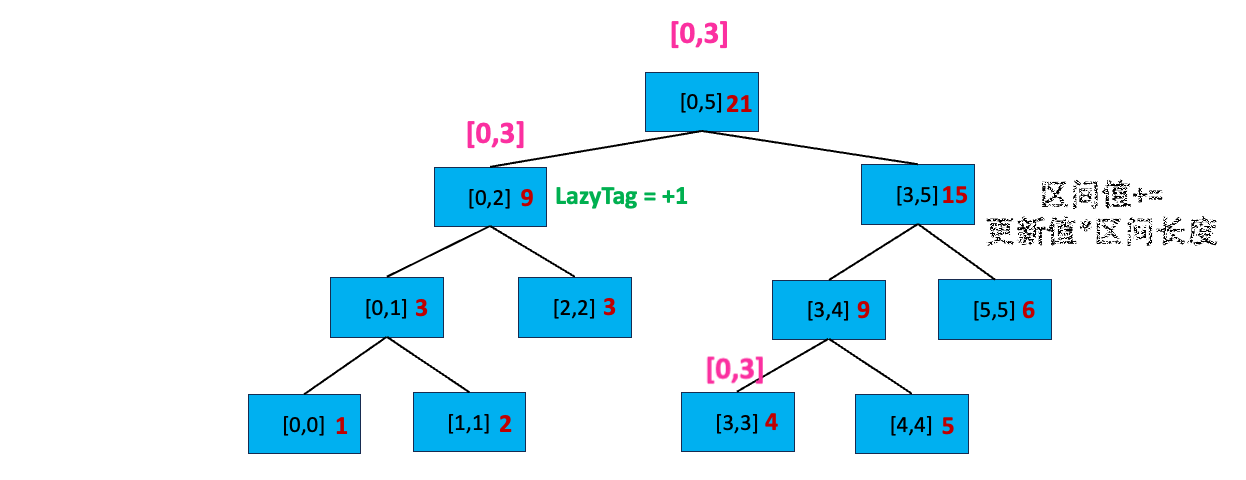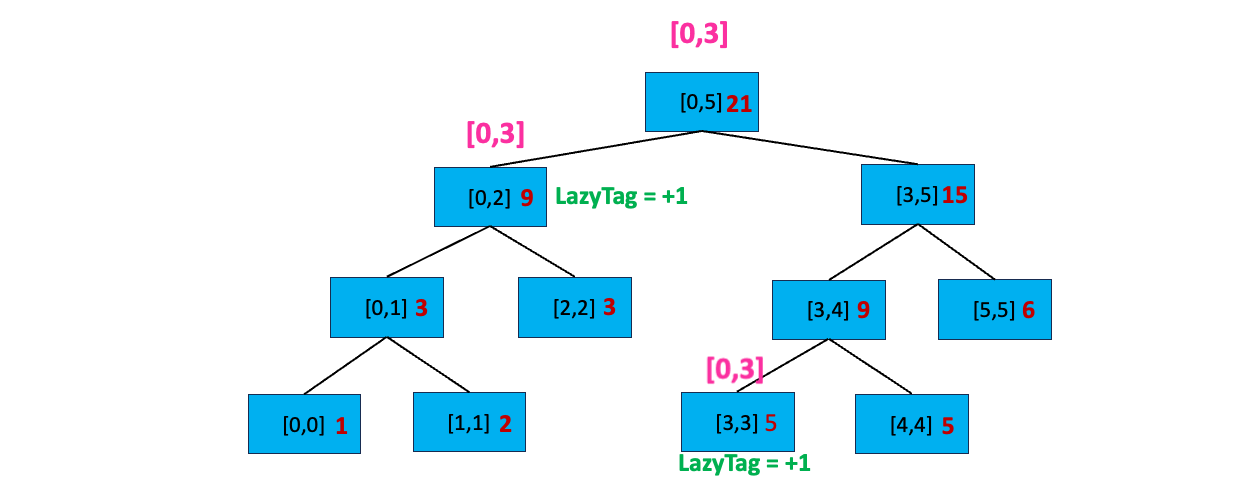
将 nums 数组[0,3] 区间中的每个数加上 1 ，加上后数组将变成 [2,3,4,5,5,6]。在线段树中，我们首先访问根节点 [0,5]，修改区间显然不完全覆盖区间[0,5]，且当前节点不存在延迟标记；我们再看当前节点的左孩子[0,2]，很显然 [0,3] 与 [0,2] 存在交集，搜索左孩子：
接着，我们来搜索 [0,2] 左孩子，首先 [0,3] 完全覆盖 [0,2]，那么我们更新这个区间，因为节点记录的是求和，而我们要对这个区间的每个数加上 1 ，那么总和 sum = sum + 1 * 区间长度，也就是 sum = 6 + (2 - 0 + 1) * 1 = 9；接下来，我们给节点打上延迟标记 LazyTag = + 1，表示这个节点的子节点都还没进行 +1 操作。


搜索完了[0,2]左孩子，我们又看到[0,3] 与[0,5] 的右孩子[3,5] 存在交集，我们开始搜索右孩子：首先，[0,3] 不覆盖[3,5] 且 [3,5] 不存在延迟标记；我们分别查看[3,5] 的左孩子和右孩子，发现其与左孩子[3,4] 有交集，开始搜索 [3,4]：


我们发现 [0,3] 不完全覆盖 [3,4]，且[3,4] 所在节点不包含延迟标记，我们搜索它的子节点。发现 [0,3] 和 [3,3] 有交集，且 [0,3] 完全覆盖[3,3]，我们更新该区间：sum = sum + 更新值 * 区间长度，即 sum = 4 + 1 * ( 3 - 3 + 1) = 5 ；然后给节点打上延迟标记 LazyTag = +1。「正是因为叶子节点也有延迟标记，还需要继续下放，也就还需要2倍的空间，因此 2 * n - 1 空间不足，需要4 * n 的空间」


至此，我们搜索完毕，开始逐层向上更新区间值：

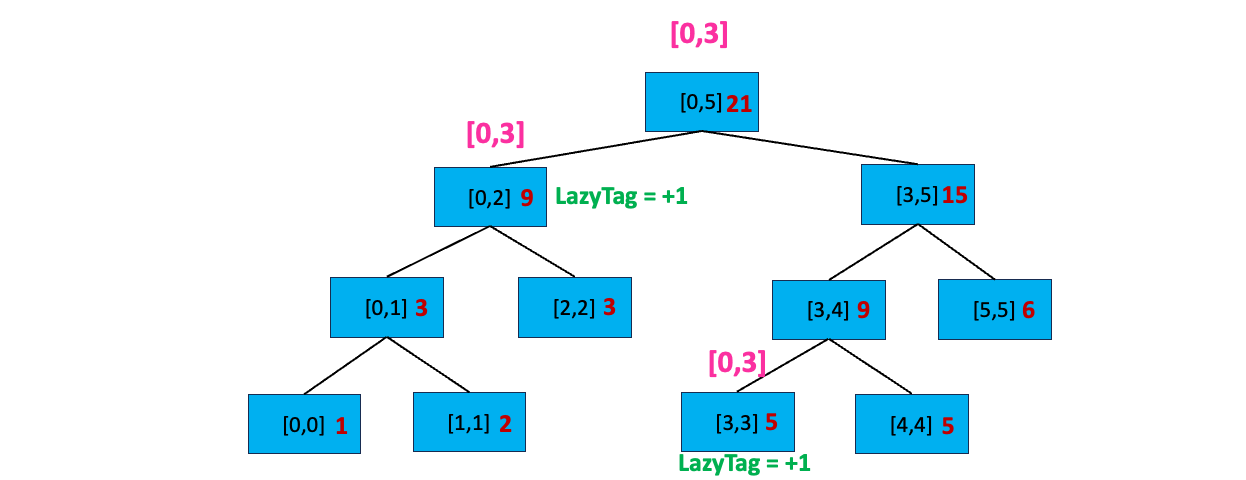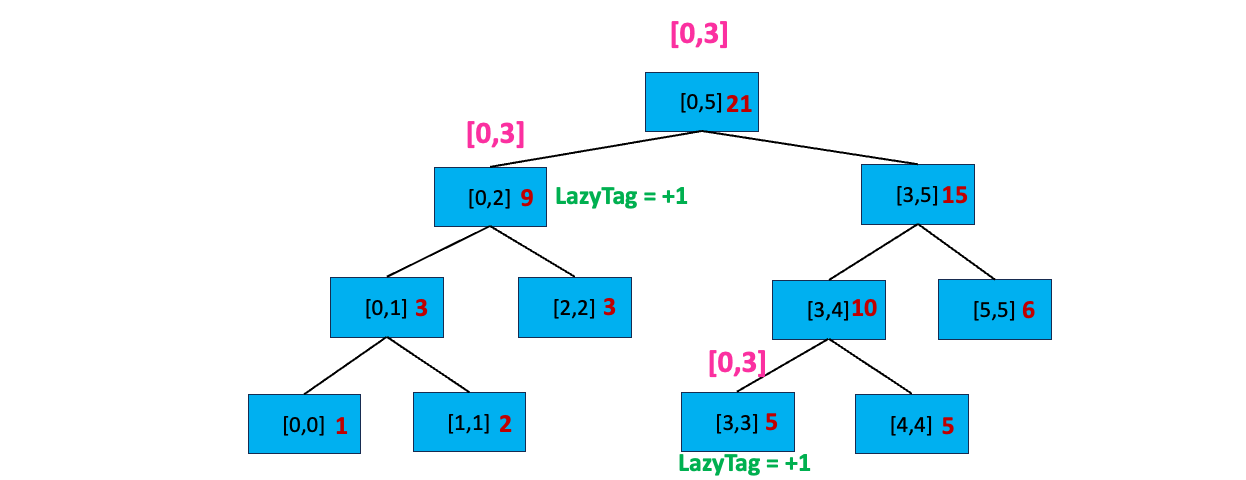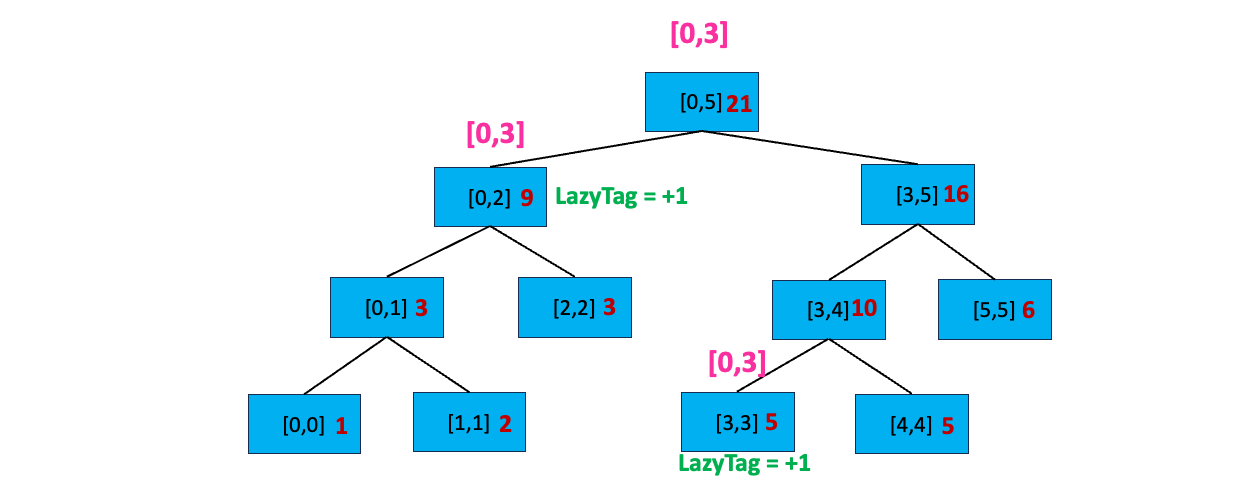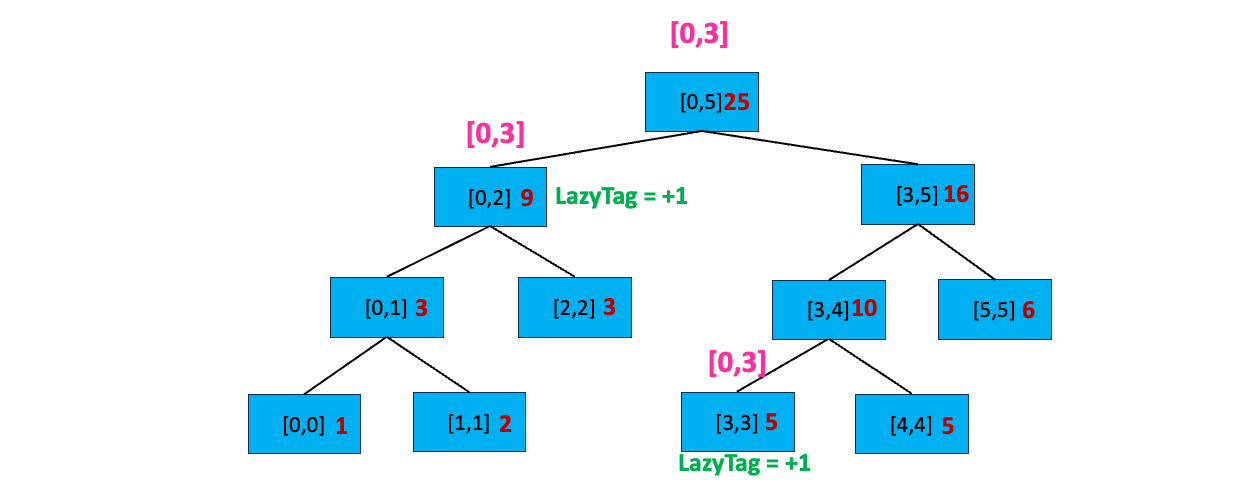
到这里，细心的你可能会发现延迟标记规则的第二条「如果没有完全覆盖，且当前区间有延迟标记，先下传延迟标记到子区间，再清除当前区间的延迟标记」在刚刚的例子中并没有出现下传延迟标记到子区间的情况。这是因为我们只进行了一次区间更新，当我们进行多次区间更新时，就会出现这个情况~~
在这里插入图片描述

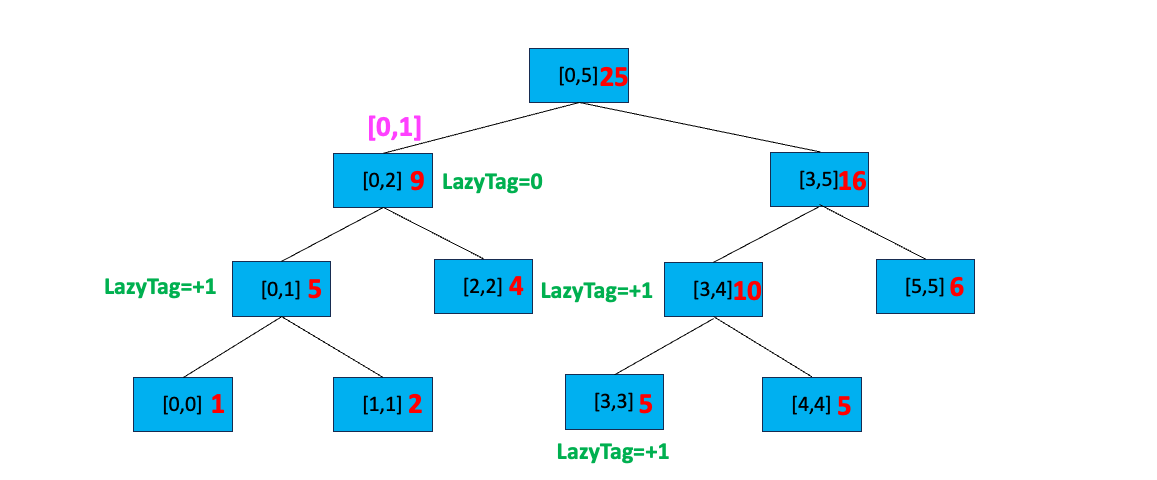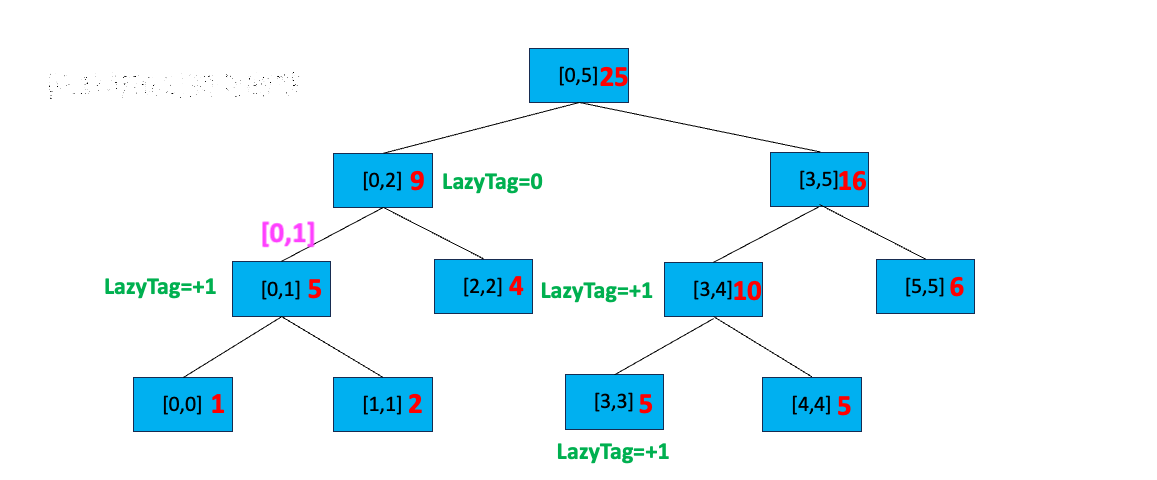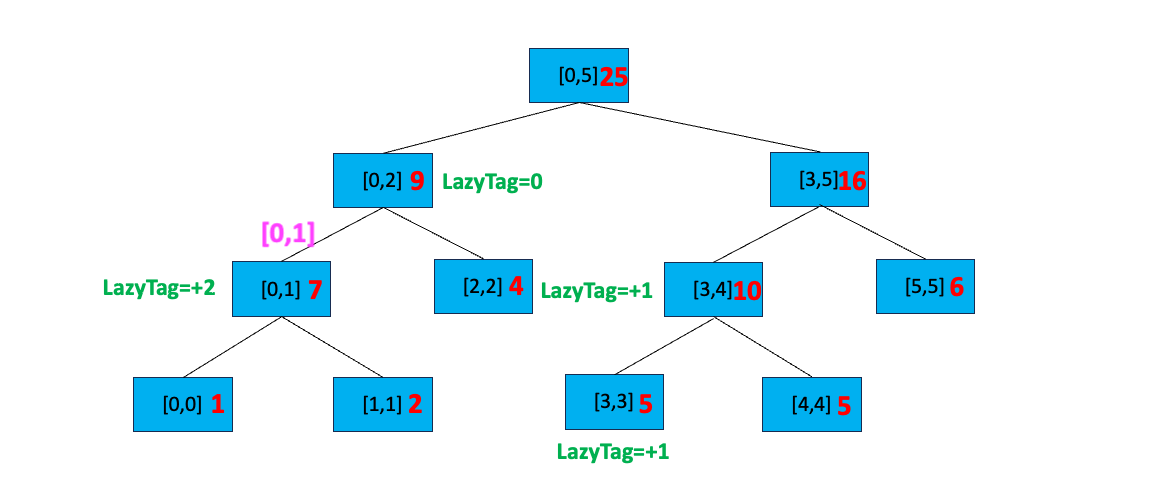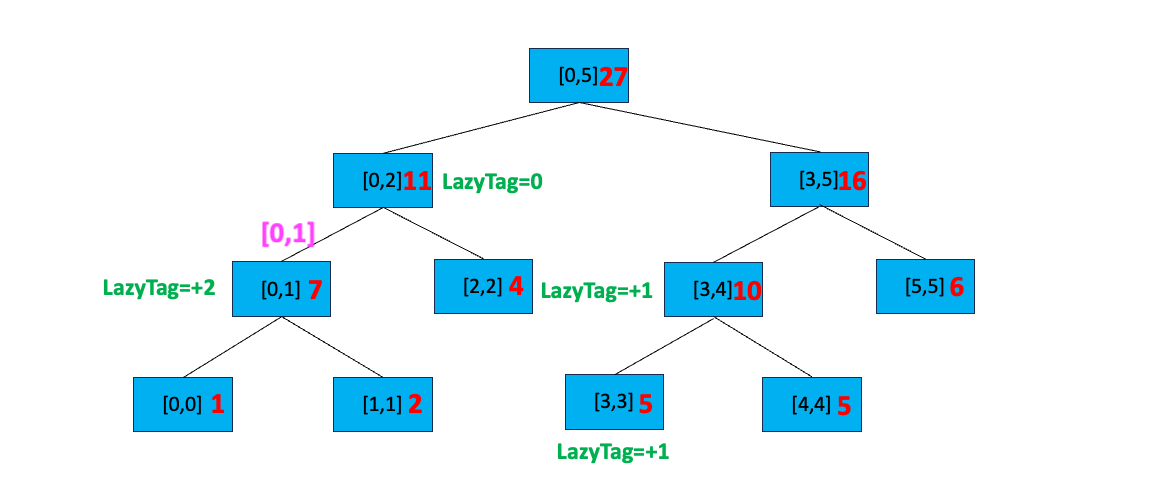
假设我们又要对区间 [0,1] 进行全部加一的更新。首先判断根节点区间与 [0,1] 区间的关系，[0,1] 不覆盖 [0,5]，我们搜索 [0,5] 的孩子节点；[0,1] 部分覆盖 [0,2] ，且 [0,2] 所在节点有延迟标记，所以我们执行以下操作：

  1. 下传延迟标记到其左右孩子节点
  2. 更新左右孩子节点的区间值，[0,1] 处更新为 sum = sum + 更新值 * 区间长度，即 sum = 3 + (1 - 0 + 1) * 1 = 5。右孩子节点 sum = 3 + (2 - 2 + 1) * 1 = 4
  3. 将当前节点的延迟标记重置为 0，即不存在延迟标记

下传延迟标记完毕。搜索与[0,2] 有交集的 [0,1] 节点，我们发现 [0,2] 完全覆盖[0,1]，直接更新 [0,1] 区间等于 5+(1-0+1)=7，添加延迟标记 LazyTag = + 1，最后向上更新区间值：

为了方便记忆，我们把区间更新的步骤简记为：完全覆盖、部分覆盖「标下下传」、搜索孩子、更新区间。下面来看看它的代码实现：

void pushUp(int index) {segTree[index] = segTree[index * 2 + 1] + segTree[index * 2 + 2]; // 向上更新，用孩子节点更新父节点
}void pushDown(int index, int left, int right) { // 向下传递延迟标记if (lazyTag[index] != 0) {int mid = (left + right) / 2;lazyTag[index * 2 + 1] += lazyTag[index]; //更新左孩子的延迟标记lazyTag[index * 2 + 2] += lazyTag[index];//更新右孩子的延迟标记segTree[index * 2 + 1] += lazyTag[index] * (mid - left + 1); // 区间值 = sum + 更新值 *（区间长度）segTree[index * 2 + 2] += lazyTag[index] * (right - mid);lazyTag[index] = 0; // 清除延迟标记}
}
public void intervalUpdate(int x, int y, int value) {intervalUpdate(0, 0, nums.length - 1, x, y, value);
}
private void intervalUpdate(int index, int left, int right, int x, int y, int value) {if (x <= left && y >= right) { // 完全覆盖segTree[index] += value * (right - left + 1); // 更新区间值lazyTag[index] += value; // 更新延迟标记return;}pushDown(index, left, right); // 部分覆盖，下传延迟标记int mid = (left + right) / 2;if (x <= mid) intervalUpdate(index * 2 + 1, left, mid, x, y, value);if (y > mid) intervalUpdate(index * 2 + 2, mid + 1, right, x, y, value);pushUp(index);
}

2.5 基于区间修改的查询

因为存在延迟标记，所以基于区间修改的查询有所不同。它遵循以下规则：

  • 当我们查询的区间完全覆盖节点区间时，直接返回区间值即可
  • 部分覆盖时，需要先下传延迟标记，再进行查询

接下来，我们看看它的代码实现~

public int query(int x, int y) {return query(0, 0, nums.length - 1, x, y);
}
private int query(int index, int left, int right, int x, int y) { // x 表示要查询的左区间，y 表示要查询的右区间if (x > right || y < left) return 0; // 如果查询区间在线段树区间外返回 0if (x <= left && y >= right) return segTree[index];  // 当查询区间包含线段树区间，返回节点值pushDown(index,left,right); //下传延迟标记int mid = (left + right) / 2;int leftQuery = query(2 * index + 1, left, mid, x, y); // 计算左孩子int rightQuery = query(2 * index + 2, mid + 1, right, x, y); // 计算右孩子return leftQuery + rightQuery; // 求和
}

与 2.3 小节中的查询相比，我们可是发现它仅仅在完全覆盖这一步之后增加了一个下传延迟标记的操纵~

3. 完整代码

最后附上完整代码和测试数据：

import java.util.List;public class Solution {int nums[] = new int[]{1, 2, 3, 4, 5, 6};int n = nums.length;int[] segTree = new int[4 * n]; // 为线段树分配空间int lazyTag[] = new int[4 * n]; // 为延迟标记分配空间void buildTree(int index, int left, int right) { // index 表示下标，left 表示左区间，right 表示右区间if (left == right) {segTree[index] = nums[left];return; // 到叶子节点就不能继续划分啦~}int mid = (left + right) / 2; // 一分为 2，例如将 [1,6] 划分为 [1,3] 和 [4,6]buildTree(2 * index + 1, left, mid); // 构建左子树，左孩子的下标为 2 * index + 1buildTree(2 * index + 2, mid + 1, right); // 构建右子树，右孩子的下标为 2 * index + 2segTree[index] = segTree[2 * index + 1] + segTree[2 * index + 2]; // 这里是求和，所以非叶子节点存储的值是左右孩子节点存储的值之和}void pushUp(int index) {segTree[index] = segTree[index * 2 + 1] + segTree[index * 2 + 2]; // 向上更新，用孩子节点更新父节点}void pushDown(int index, int left, int right) { // 向下传递延迟标记if (lazyTag[index] != 0) {int mid = (left + right) / 2;lazyTag[index * 2 + 1] += lazyTag[index]; //更新左孩子的延迟标记lazyTag[index * 2 + 2] += lazyTag[index];//更新右孩子的延迟标记segTree[index * 2 + 1] += lazyTag[index] * (mid - left + 1); // 区间值 = sum + 更新值 *（区间长度）segTree[index * 2 + 2] += lazyTag[index] * (right - mid);lazyTag[index] = 0; // 清除延迟标记}}public void intervalUpdate(int x, int y, int value) {intervalUpdate(0, 0, nums.length - 1, x, y, value);}private void intervalUpdate(int index, int left, int right, int x, int y, int value) {if (x <= left && y >= right) { // 完全覆盖segTree[index] += value * (right - left + 1); // 更新区间值lazyTag[index] += value; // 更新延迟标记return;}pushDown(index, left, right); // 部分覆盖，下传延迟标记int mid = (left + right) / 2;if (x <= mid) intervalUpdate(index * 2 + 1, left, mid, x, y, value);if (y > mid) intervalUpdate(index * 2 + 2, mid + 1, right, x, y, value);pushUp(index);}// 区间查询public int query(int x, int y) {return query(0, 0, nums.length - 1, x, y);}private int query(int index, int left, int right, int x, int y) { // x 表示要查询的左区间，y 表示要查询的右区间if (x > right || y < left) return 0; // 如果查询区间在线段树区间外返回 0if (x <= left && y >= right) return segTree[index];  // 当查询区间包含线段树区间，返回节点值pushDown(index, left, right); //下传延迟标记int mid = (left + right) / 2;int leftQuery = query(2 * index + 1, left, mid, x, y); // 计算左孩子int rightQuery = query(2 * index + 2, mid + 1, right, x, y); // 计算右孩子return leftQuery + rightQuery; // 求和}public static void main(String[] args) {Solution solution = new Solution();solution.buildTree(0, 0, solution.nums.length - 1);solution.intervalUpdate(0,3,1);solution.intervalUpdate(1,2,1);System.out.println(solution.query(0, 2));}
}

能看到最后，你真的很棒，加油~


本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/12873.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

如何降低TCP在局域网环境下的数据传输延迟

如何降低TCP在局域网环境下的数据传输延迟

以Ping为例。本案例是一个测试题目&#xff0c;只有现象展示&#xff0c;不含解决方案。 ROS_Kinetic_26 使用rosserial_windows实现windows与ROS master发送与接收消息_windows 接收ros1 消息 什么是ping&#xff1f; AI&#xff1a; ping是互联网控制消息协议&#xff08;…
阅读更多...
【Spring Boot】

【Spring Boot】

目录 &#x1f36a;1 Spring Boot 的创建 &#x1f382;2 简单 Spring Boot 程序 &#x1f370;3 Spring Boot 配置文件 &#x1f36e;3.1 properties 基本语法 &#x1fad6;3.2 yml 配置文件说明 &#x1f36d;3.2.1 yml 基本语法 &#x1f369;3.3 配置文件里的配置类…
阅读更多...
如何将ubuntu LTS升级为Pro

如何将ubuntu LTS升级为Pro

LTS支持周期是5年&#xff1b; Pro支持周期是10年。 Ubuntu Pro专业版笔记 步骤&#xff1a; 打开“软件和更新” 可以看到最右侧的标签是Ubuntu Pro。 在没有升级之前&#xff0c;如果使用下面两步&#xff1a; sudo apt updatesudo apt upgrade 出现如下提示&#xff…
阅读更多...
【低代码专题方案】iPaaS运维方案，助力企业集成平台智能化高效运维

【低代码专题方案】iPaaS运维方案，助力企业集成平台智能化高效运维

01 场景背景 随着IT行业的发展和各家企业IT建设的需要&#xff0c;信息系统移动化、社交化、大数据、系统互联、数据打通等需求不断增多&#xff0c;企业集成平台占据各个企业领域&#xff0c;成为各业务系统数据传输的中枢。 集成平台承接的业务系统越多&#xff0c;集成平台…
阅读更多...
【数据结构】时间复杂度和空间复杂度

【数据结构】时间复杂度和空间复杂度

&#x1f4d9; 作者简介 &#xff1a;RO-BERRY &#x1f4d7; 学习方向&#xff1a;致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 &#x1f4d2; 日后方向 : 偏向于CPP开发以及大数据方向&#xff0c;欢迎各位关注&#xff0c;谢谢各位的支持 时间复杂度和空间复杂度 前…
阅读更多...
diffusion model（五）stable diffusion底层原理（latent diffusion model， LDM）

diffusion model（五）stable diffusion底层原理（latent diffusion model， LDM）

LDM: 在隐空间用diffusion model合成高质量的图片&#xff01; [论文地址] High-Resolution Image Synthesis with Latent Diffusion Models [github] https://github.com/compvis/latent-diffusion 文章目录 LDM: 在隐空间用diffusion model合成高质量的图片&#xff01;系列…
阅读更多...
某ERP系统信息泄露登录后台

某ERP系统信息泄露登录后台

漏洞描述 某ERP前台泄露了某api接口，恶意攻击者可通过调用该接口，对用户的账号和密码进行非授权访问，在获取到账号和密码后，恶意攻击者可接管后台。 免责声明 技术文章仅供参考，任何个人和组织使用网络应当遵守宪法法律，遵守公共秩序，尊重社会公德，不得利用网络从事…
阅读更多...
时间复杂度介绍及其计算

时间复杂度介绍及其计算

时间复杂度 1.算法效率 如何衡量一个算法的好坏呢&#xff1f;看这段代码&#xff1a; long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); }这是斐波那契数列的递归代码&#xff0c;非常简洁&#xff0c;那么这就一定说明它好吗&#xff1f;答案显而易…
阅读更多...
Stable Diffusion - 扩展 SegmentAnything 和 GroundingDINO 实例分割算法 插件的配置与使用

Stable Diffusion - 扩展 SegmentAnything 和 GroundingDINO 实例分割算法 插件的配置与使用

欢迎关注我的CSDN&#xff1a;https://spike.blog.csdn.net/ 本文地址&#xff1a;https://blog.csdn.net/caroline_wendy/article/details/131918652 Paper and GitHub&#xff1a; Segment Anything: SAM - Segment Anything GitHub: https://github.com/facebookresearch/s…
阅读更多...
【源码解析】SpringBoot循环依赖源码解析II

【源码解析】SpringBoot循环依赖源码解析II

前言 前面已经写过循环以来的分析&#xff0c;对循环依赖有一些了解&#xff0c;【源码解析】Spring循环依赖和三级缓存。简单回顾一下&#xff1a; Spring可以解决Autowired注入的循环依赖 Spring解决不了构造器注入的循环依赖 使用Aysnc注解会导致循环依赖。提前暴露的Bea…
阅读更多...
LeetCode 刷题 数据结构 数组 485 最大连续1的个数

LeetCode 刷题 数据结构 数组 485 最大连续1的个数

给定一个二进制数组 nums &#xff0c; 计算其中最大连续 1 的个数。 示例 1&#xff1a; 输入&#xff1a;nums [1,1,0,1,1,1] 输出&#xff1a;3 解释&#xff1a;开头的两位和最后的三位都是连续 1 &#xff0c;所以最大连续 1 的个数是 3.示例 2: 输入&#xff1a;nums […
阅读更多...
C语言中的函数（超详细）

C语言中的函数（超详细）

C语言中的函数&#xff08;超详细&#xff09; 一、函数概述二、C语言中函数的分类1.库函数2.自定义函数三、函数的参数1.实际参数&#xff08;实参&#xff09;2.形式参数&#xff08;形参&#xff09;四、函数的调用1.传值调用2.传址调用五、函数的嵌套调用和链式访问1.嵌套调…
阅读更多...
大于号在python中怎么打,python大于等于怎么写

大于号在python中怎么打,python大于等于怎么写

大家好&#xff0c;小编为大家解答python中大于并小于一个数代码的问题。很多人还不知道python中大于等于且小于等于&#xff0c;现在让我们一起来看看吧&#xff01; 1、python 中不等于怎么表示 #!/usr/bin/python a1 b2 if ab: print "a 等于 b" if a!b: print &…
阅读更多...
【playbook】Ansible的脚本----playbook剧本

【playbook】Ansible的脚本----playbook剧本

Ansible的脚本----playbook剧本 1.playbook剧本组成2.playbook剧本实战演练2.1 实战演练一&#xff1a;给被管理主机安装Apache服务2.2 实战演练二&#xff1a;使用sudo命令将远程主机的普通用户提权为root用户2.3 实战演练三&#xff1a;when条件判断指定的IP地址2.4 实战演练…
阅读更多...
图文教程：如何在 3DS Max 中创建3D迷你卡通房屋

图文教程：如何在 3DS Max 中创建3D迷你卡通房屋

推荐&#xff1a; NSDT场景编辑器助你快速搭建可二次开发的3D应用场景 在本教程中&#xff0c;我们将学习如何创建一个有趣的、低多边形的迷你动画房子&#xff0c;你可以在自己的插图或视频游戏项目中使用它。您将学习的一些技能将包括创建基本的3D形状和基本的建模技术。让我…
阅读更多...
IP网络对讲求助模块

IP网络对讲求助模块

SV-6002 IP网络对讲求助模块是一款壁挂式一键求助对讲模块&#xff0c;具有10/100M以太网接口&#xff0c;其接收网络的音频数据&#xff0c;实时解码播放&#xff0c;还配置了麦克风输入和扬声器功放输出。SV-6002模块可实现对讲、广播、等功能&#xff0c;作为网络广播对讲系…
阅读更多...
Docker Compose 容器编排 + Docker--harbor私有仓库部署与管理

Docker Compose 容器编排 + Docker--harbor私有仓库部署与管理

目录 一、Docker Compose简介 1、Docker Compose 的YAML 文件格式及编写注意事项 2、Docker compose 使用的三个步骤 3、 Docker Compose配置常用字段 4、 Docker Compose 常用命令 5、 Docker Compose 文件结构 二&#xff1a; Docker Compose 安装 1、Docker Compose…
阅读更多...
FreeRTOS之互斥量

FreeRTOS之互斥量

什么是互斥量&#xff1f; 在多数情况下&#xff0c;互斥型信号量和二值型信号量非常相似&#xff0c;但是从功能上二值型信号量用于同步&#xff0c; 而互斥型信号量用于资源保护。 互斥型信号量和二值型信号量还有一个最大的区别&#xff0c;互斥型信号量可以有效解决优先级…
阅读更多...
合作客户销售数据可视化分析

合作客户销售数据可视化分析

以一个案例进行实际分析&#xff1a; 数据来源&#xff1a;【地区数据分析】 以此数据来制作报表。 技巧一&#xff1a;词云图 以城市名称来显示合同金额的分布&#xff0c;合同金额越大&#xff0c;则城市文字显示越大。 技巧二&#xff1a;饼图 下面制定一个&#xff0c;合…
阅读更多...
热备份路由协议原理

热备份路由协议原理

热备份路由协议原理 HSRP协议/VRRP协议热备份协议 热备份协议&#xff08;Hot Standby Protocol&#xff09; 是一种基于冗余设计的协议&#xff0c;用于提高网络的可靠性和冗余性。它允许多个设备共享同一个IP地址&#xff0c;其中一个设备被选为主设备&#xff0c;其他设备…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023