笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~
笔记链接
【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础
吴恩达课程笔记——浅层神经网络、深层神经网络
- 四、浅层神经网络
- 1.双层神经网络表示
- 2.双层神经网络的前向传播
- 第一层前向传播
- 第二层前向传播
- 3.双层神经网络的反向传播
- 参数
- 梯度下降
- 反向传播公式
- 第二层反向传播推导
- 4.激活函数
- 5.为什么要使用非线性激活函数?
- 6.为什么要对W随机初始化?
- 五、深层神经网络
- 1.变量定义
- 2.矩阵的维数
- 3.为什么使用深层表示(Deep Representation)
- 4.深层神经网络块图解
- 5.深层神经网络前向和反向传播的实现
四、浅层神经网络
1.双层神经网络表示


x1 ,x2 ,x3:输入层A[0],指的是单个样本的输入值
中间四个神经元:隐藏层A[1]
右侧的单个神经元:输出层A[2]
单次训练过程:
-
正向传播
- 训练样本分别对隐藏层的各神经元的参数(w向量和b值)进行计算得到z[1]
- 各神经元的z放到一起组成Z[1]
- z[1]激活后得到a
- 各神经元的a放到一起组成A[1]
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 1 [ 1 ] = σ ( z 2 [ 1 ] ) z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 2 ] , a 1 [ 1 ] = σ ( z 3 [ 1 ] ) z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 1 [ 1 ] = σ ( z 4 [ 1 ] ) z^{[1]}_{1}=w^{[1]T}_{1}x+b^{[1]}_{1},a^{[1]}_{1}=σ(z^{[1]}_{1})\\ z^{[1]}_{2}=w^{[1]T}_{2}x+b^{[1]}_{2},a^{[1]}_{1}=σ(z^{[1]}_{2})\\ z^{[1]}_{3}=w^{[1]T}_{3}x+b^{[2]}_{3},a^{[1]}_{1}=σ(z^{[1]}_{3})\\ z^{[1]}_{4}=w^{[1]T}_{4}x+b^{[1]}_{4},a^{[1]}_{1}=σ(z^{[1]}_{4})\\ z1[1]=w1[1]Tx+b1[1],a1[1]=σ(z1[1])z2[1]=w2[1]Tx+b2[1],a1[1]=σ(z2[1])z3[1]=w3[1]Tx+b3[2],a1[1]=σ(z3[1])z4[1]=w4[1]Tx+b4[1],a1[1]=σ(z4[1])

- 各神经元的A[1]再作为训练样本对对输出层的单个神经元的参数(w向量和b值)进行计算得到z[2]
- z[2]激活得到a[2]
Z [ 1 ] = W [ 1 ] X + b [ 1 ] A [ 1 ] = σ ( Z [ 1 ] ) Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A [ 2 ] = σ ( Z [ 2 ] ) Z^{[1]}=W^{[1]}X+b^{[1]}\\ A^{[1]}=σ(Z^{[1]})\\ Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}\\ A^{[2]}=σ(Z^{[2]}) Z[1]=W[1]X+b[1]A[1]=σ(Z[1])Z[2]=W[2]A[1]+b[2]A[2]=σ(Z[2])
-
反向传播
- 从输出结果到第二层到第一层依次计算对成本函数的导数,达到对各个w、b的迭代、训练效果
2.双层神经网络的前向传播
多个样本
训练样本集:X = [x(1),x(2),x(3), … ,x(m)],其中x(i)是第 i 个训练样本,共m个样本
n[0]:第n层的单元数,n[0]表示特征向量x的维度
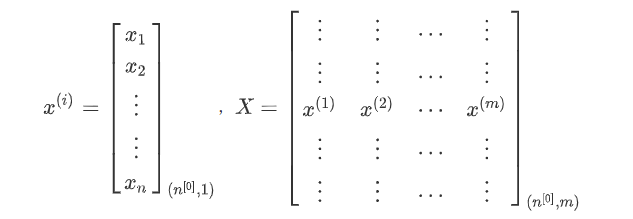
第一层前向传播
第一层神经元的w参数集:

第一层神经元的b参数集:
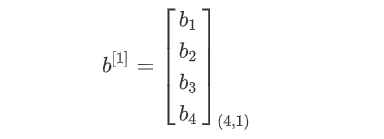
第一层前向传播过程计算Z[1]
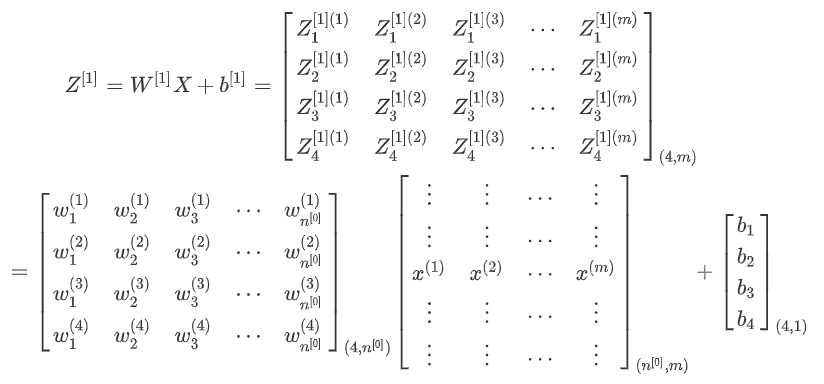
第一层前向传播过程计算A[1]
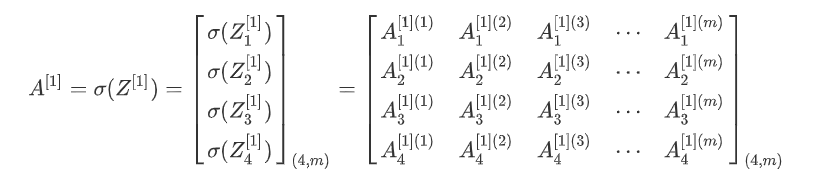
第二层前向传播
第二层神经元的w参数集:
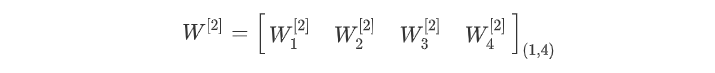
第二层神经元的b参数集:
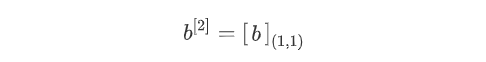
第二层前向传播过程计算Z[2]

第二层前向传播过程计算A[2]
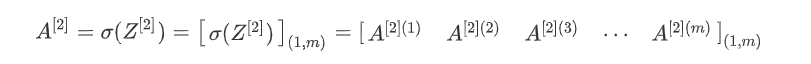
核对矩阵维数
第一层 X . s h a p e = ( n [ 0 ] , m ) W [ 1 ] . s h a p e = ( n [ 1 ] , n [ 0 ] ) b [ 1 ] . s h a p e = ( n [ 1 ] , 1 ) Z [ 1 ] . s h a p e = ( n [ 1 ] , m ) A [ 1 ] . s h a p e = ( n [ 1 ] , m ) 第二层 W [ 2 ] . s h a p e = ( n [ 2 ] , n [ 1 ] ) Z [ 2 ] . s h a p e = ( n [ 2 ] , m ) A [ 2 ] . s h a p e = ( n [ 2 ] , m ) Y . s h a p e = A [ 2 ] . s h a p e = ( n [ 2 ] , m ) \textcolor{red}{第一层}\\ X.shape=(n^{[0]},m)\\ W^{[1]}.shape=(n^{[1]},n^{[0]})\\ b^{[1]}.shape=(n^{[1]},1)\\ Z^{[1]}.shape=(n^{[1]},m)\\ A^{[1]}.shape=(n^{[1]},m)\\ \textcolor{red}{第二层} \\ W^{[2]}.shape=(n^{[2]},n^{[1]})\\ Z^{[2]}.shape=(n^{[2]},m)\\ A^{[2]}.shape=(n^{[2]},m)\\ Y.shape=A^{[2]}.shape=(n^{[2]},m) 第一层X.shape=(n[0],m)W[1].shape=(n[1],n[0])b[1].shape=(n[1],1)Z[1].shape=(n[1],m)A[1].shape=(n[1],m)第二层W[2].shape=(n[2],n[1])Z[2].shape=(n[2],m)A[2].shape=(n[2],m)Y.shape=A[2].shape=(n[2],m)
3.双层神经网络的反向传播
参数
训练样本维数: n [ 0 ] 隐藏层神经元个数: n [ 1 ] 输出层神经元个数: n [ 2 ] = 1 W [ 1 ] : ( n [ 1 ] , n [ 0 ] ) b [ 1 ] : ( n [ 1 ] , 1 ) W [ 2 ] : ( n [ 2 ] , n [ 1 ] ) b [ 2 ] : ( n [ 2 ] , 1 ) 成本函数: J ( W , b ) = 1 m ∑ i = 1 m L ( y ^ i , y i ) 训练样本维数:n^{[0]} \\ 隐藏层神经元个数:n^{[1]} \\ 输出层神经元个数:n^{[2]}=1 \\ W^{[1]}:(n^{[1]},n^{[0]})\\ b^{[1]}:(n^{[1]},1)\\ W^{[2]}:(n^{[2]},n^{[1]})\\ b^{[2]}:(n^{[2]},1)\\ 成本函数:J(W,b)=\frac{1}{m}\sum_{i=1}^{m}{L(ŷ_i,y_i)} 训练样本维数:n[0]隐藏层神经元个数:n[1]输出层神经元个数:n[2]=1W[1]:(n[1],n[0])b[1]:(n[1],1)W[2]:(n[2],n[1])b[2]:(n[2],1)成本函数:J(W,b)=m1i=1∑mL(y^i,yi)
梯度下降
d W [ i ] = ∂ J ∂ W [ i ] , d b [ i ] = ∂ J ∂ b [ i ] W [ i ] = W [ i ] − α d W [ i ] b [ i ] = b [ i ] − α d b [ i ] i = 1 , 2 dW^{[i]}=\frac{\partial J}{\partial W^{[i]}},db^{[i]}=\frac{\partial J}{\partial b^{[i]}}\\ W^{[i]}=W^{[i]}-\alpha dW{[i]} \\ b^{[i]}=b^{[i]}-\alpha db{[i]}\\ i=1,2 dW[i]=∂W[i]∂J,db[i]=∂b[i]∂JW[i]=W[i]−αdW[i]b[i]=b[i]−αdb[i]i=1,2
反向传播公式
d Z [ 2 ] = A [ 2 ] − Y d W [ 2 ] = 1 m d Z [ 2 ] A [ 1 ] T d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) d Z [ 1 ] = W [ 2 ] T d Z [ 1 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) d W [ 1 ] = 1 m d Z [ 1 ] X T d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) dZ^{[2]}=A^{[2]}-Y\\ dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T}\\ db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True)\\ dZ^{[1]}=W^{[2]T}dZ^{[1]}*g^{[1]'}(Z^{[1]})\\ dW^{[1]}=\frac{1}{m}dZ^{[1]}X^{T}\\ db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True)\\ dZ[2]=A[2]−YdW[2]=m1dZ[2]A[1]Tdb[2]=m1np.sum(dZ[2],axis=1,keepdims=True)dZ[1]=W[2]TdZ[1]∗g[1]′(Z[1])dW[1]=m1dZ[1]XTdb[1]=m1np.sum(dZ[1],axis=1,keepdims=True)
第二层反向传播推导

4.激活函数
-
sigmoid:只可能用于二元分类的输出层。
a = 1 1 + e − z d a d z = a ( 1 − a ) a=\frac{1}{1+e^{-z}}\\ \frac{da}{dz}=a(1-a) a=1+e−z1dzda=a(1−a)

-
tanh:几乎在所有情况下优于sigmoid函数。(计算速度更快)
a = e z − e − z e z + e − z d a d z = 1 − a 2 a=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\\ \frac{da}{dz}=1-a^2 a=ez+e−zez−e−zdzda=1−a2

-
ReLU(Rectified Linear Unit):最常用的默认激活函数
a = m a x ( 0 , z ) d a d z = { 0 , z < 0 1 , z > 0 u n d e f i n e d , z = 0 a=max(0,z)\\ \frac{da}{dz}=\left\{ \begin{aligned} 0 & , z<0 \\ 1 & , z>0 \\ undefined&,z=0 \end{aligned} \right. a=max(0,z)dzda=⎩ ⎨ ⎧01undefined,z<0,z>0,z=0

-
leaky ReLU:有人认为这个比ReLU好
a = m a x ( α z , z ) , α u s u a l l y l e s s t h a n 1 d a d z = { α , z < 0 1 , z > 0 u n d e f i n e d , z = 0 a=max(\alpha z,z),\alpha \ usually \ less\ than\ 1\\ \frac{da}{dz}=\left\{ \begin{aligned} \alpha & , z<0 \\ 1 & , z>0 \\ undefined&,z=0 \end{aligned} \right. a=max(αz,z),α usually less than 1dzda=⎩ ⎨ ⎧α1undefined,z<0,z>0,z=0

5.为什么要使用非线性激活函数?
- 解决线性不可分问题:线性激活函数(如恒等映射)只能产生线性变换,无法处理非线性可分的问题。
- 增强模型的表达能力:非线性激活函数能够引入非线性变换,使得神经网络能够学习更加复杂的模式和特征。
- 防止梯度消失:在深层神经网络中,使用线性激活函数会导致梯度逐层地缩小,进而导致梯度消失的问题。
- 增加模型的非线性响应:非线性激活函数可以引入非线性响应,使得模型能够更好地适应数据的非线性特征。这对于处理图像、语音等复杂数据具有重要意义,能够提高模型的性能。
只有一种情况可能使用线性激活函数:在输出层。
6.为什么要对W随机初始化?
- 如果把W初始化为全部为0,那么第一层上的神经元训练后都将是相同的,其下一层的神经元对上一层的判断权重也是完全相同的,同时这一层的神经元也会是完全相同的。由归纳法,每一层上的神经元都是完全相同的。这样就丧失了多层神经网络的判断性能优势。
- 初始化时应该使W中的数字尽量小,以使得sigmoid或tanh计算导数时处于导数较大的区域,以保证迭代学习的速度
五、深层神经网络
1.变量定义
| 变量名 | 变量含义 |
|---|---|
| l | 层数 |
| n[l] | l 层的单元数 |

2.矩阵的维数
| 矩阵符号 | 矩阵维数 |
|---|---|
| X | (n[0],m) |
| W[l] and dW[l] | (n[l],n[l-1]) |
| b[l] and db[l] | (n[l],1) |
| Z[l] and dZ[l] | (n[l],m) |
| A[l] and dA[l] | (n[l],m) |
| Y | (n[the last l ],m) |
3.为什么使用深层表示(Deep Representation)
深层表示(Deep Representation)是神经网络中的一个重要概念,它指的是通过多层非线性变换来逐步提取输入数据的高级特征表示。
以下是使用深层表示的几个主要原因:
- 特征表达能力增强:深层表示可以通过逐层的非线性变换,将原始输入数据转化为更高级别的抽象特征表示。每一层都可以学习到数据的不同抽象层次的特征,使得模型能够更好地捕捉输入数据中的结构和模式。相比于浅层模型,深层表示具有更强大的特征表达能力。
- 特征的层次化表示:深层表示可以将输入数据的特征表示分解为多个层次,每一层都对应着不同抽象层次的特征。这种层次化的特征表示使得模型能够更好地理解数据的结构和语义,从而提高模型的泛化能力和鲁棒性。
- 梯度传播更有效:在深层网络中,通过反向传播算法计算梯度时,梯度可以更容易地传播到较早的层。这是因为深层网络中的参数共享和权重共享的结构,使得梯度能够通过多个层级的连接路径传递。相比于浅层网络,深层网络可以更有效地利用梯度信息进行参数更新,从而提高模型的训练效率和性能。
- 数据表示的可分离性:深层表示可以将输入数据的不同方面进行分离和表示。例如,在图像处理任务中,底层的卷积层可以学习到边缘和纹理等低级特征,而高层的全连接层可以学习到物体的形状和类别等高级特征。这种分离性使得模型能够更好地对不同方面的特征进行建模和学习。
4.深层神经网络块图解


5.深层神经网络前向和反向传播的实现
前向传播
A [ 0 ] = X Z [ l ] = W [ 1 ] A [ l − 1 ] + b [ l ] A [ l ] = g [ l ] ( Z [ l ] ) A^{[0]}=X\\ Z^{[l]}=W^{[1]}A^{[l-1]}+b^{[l]}\\ A^{[l]}=g^{[l]}(Z^{[l]})\\ A[0]=XZ[l]=W[1]A[l−1]+b[l]A[l]=g[l](Z[l])
反向传播
d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] ) d W [ l ] = 1 m d Z [ l ] A [ l − 1 ] T d b [ l ] = 1 m n p . s u m ( d Z [ l ] , a x i s = 1 , k e e p d i m s = T r u e ) d A [ l − 1 ] = W [ l ] T d Z [ l ] \textcolor{red}{}\\ dZ^{[l]}=dA^{[l]}*g^{[l]'}(Z^{[l]})\\ dW^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}\\ db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims=True)\\ dA^{[l-1]}=W^{[l]T}dZ^{[l]} dZ[l]=dA[l]∗g[l]′(Z[l])dW[l]=m1dZ[l]A[l−1]Tdb[l]=m1np.sum(dZ[l],axis=1,keepdims=True)dA[l−1]=W[l]TdZ[l]
——面试时Set常见问题解读 结合源码分析)



)



)



无人机技术)






