目录

1 主要内容

主从博弈模型

基于元模型的均衡算法流程图

2 部分代码

3 程序结果

4 下载链接

---

1 主要内容

该程序复现《基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理》模型，建立运营商和多虚拟电厂的一主多从博弈模型，研究运营商动态定价行为和虚拟电厂能量管理模型，模型为双层，首先下层模型中，构建了多个虚拟电厂的联合调度模型，以每个虚拟电厂的运行成本最低为优化目标，而上层为领导者模型，主要是优化市场运营商的电价，包括售电电价和购电电价的优化，从而构成了主从博弈模型，在求解的过程中，上层采用的是粒子群算法，而下层则是调用CPLEX求解器进行求解，由于模型整体规模较大，故采用了元模型算法加速求解。程序采用matlab+cplex求解，注释清楚，运行可靠，方便学习参考！

• 主从博弈模型

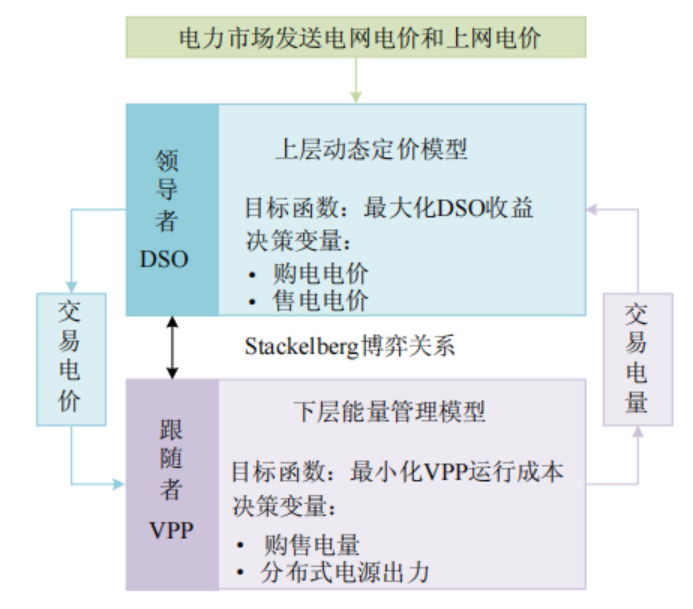
说明：将 DSO 和 VPP 的拥有者视为博弈的参与者。其中，DSO充当领导者，汇总各 VPP 上报的购售电量，结合上网电价和电网电价，考虑VPP 的价格响应行为，以最大化自身收益为目标为各VPP 制定交易电价；各VPP 充当跟随者，接收 DSO 制定的交易电价，合理安排内部各DER 出力，以最小化运行成本为目标制定与运营商交易的电量。领导者与跟随者之间顺次博弈，构成 Stackelberg 博弈，各 VPP 之间同时决策，形成非合作博弈。

• 基于元模型的均衡算法流程图

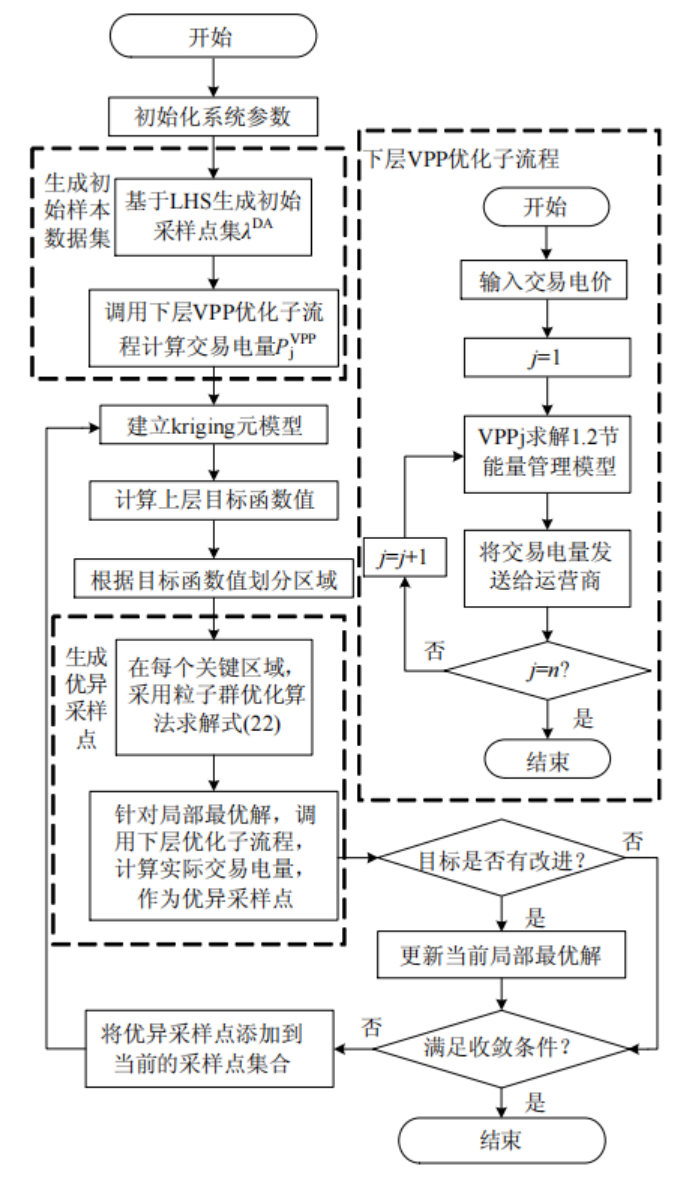
该文章通过引入元模型提高系统运算速度作为一大亮点，这给我们创新提供了一个很好的思路，大家可以关注一下数学优化理论方面的新方法，将其应用于自建模型中，成为一个重要创新点。

2 部分代码

%% 算法总参数设定
Number=5; 
%% 根据超拉丁采样(LHS)生成Number个初始样本点
lambda_Wb=[0.40*ones(1,7),0.75*ones(1,4),1.20*ones(1,3),0.75*ones(1,4),1.20*ones(1,4),0.40*ones(1,2)];
% % lambda_Ws = 0.4*ones(1,24);
lambda_Ws=[0*ones(1,7),0.35*ones(1,4),0.5*ones(1,3),0.35*ones(1,4),0.5*ones(1,4),0*ones(1,2)];
​
%通过LHS生成样本点
for t=1:24temp=lhsdesign(Number,1); %生成每个时段的抽样中间辅助矩阵,为1维分Number层的超拉丁抽样结果lambda_DAs(:,t)=temp.*(lambda_Wb(t)-lambda_Ws(t))+lambda_Ws(t); %生成运营商制定的售电价格lambda_DAb(:,t)=lambda_DAs(:,t)+rand(Number,1).*(lambda_Wb(t)-lambda_DAs(:,t)); %生成运营商制定的购电价格(购电价应大于售电价所以这么写)
end
disp('超拉丁采样(LHS)生成Number个初始样本点,结束！')
%% 通过生成的样本点调用下层博弈模型,计算出每个VPP的交易电量来构成样本数据集
for i=1:Number[P_VPP_s1,P_VPP_b1,~]=Fun_VPP1(lambda_DAb(i,:),lambda_DAs(i,:));[P_VPP_s2,P_VPP_b2,~]=Fun_VPP2(lambda_DAb(i,:),lambda_DAs(i,:));[P_VPP_s3,P_VPP_b3,~]=Fun_VPP3(lambda_DAb(i,:),lambda_DAs(i,:));P_VPP_s(i,:)=[P_VPP_s1,P_VPP_s2,P_VPP_s3];P_VPP_b(i,:)=[P_VPP_b1,P_VPP_b2,P_VPP_b3];
end
disp('样本数据集构成,结束！')
%% 修正Kriging模型,计算每组样本点对应的目标函数值
for i=1:Number[C_DSO(i,1)]=Fun_DSO(lambda_DAs(i,:),lambda_DAb(i,:),P_VPP_b(i,:),P_VPP_s(i,:));
end
disp('计算每组样本点对应的目标函数值,结束！')
%% 关键区域划分,并计算各个区域的最优值
l=1; %划分的区域的编号,初始化为1(编号越小,说明该区域包含最优解的概率越大) 
S=C_DSO; %设定S为所有电价样本对应的上层目标函数值集
for i=1:Numberlambda_DA(i,:)=[lambda_DAs(i,:),lambda_DAb(i,:)]; %将售卖电价统一放入lambda_DA中存储
end
X=lambda_DA; %设定X为所有电价样本点集
SL=lambda_DA; %后续计算半径r中用于生成电价上下边界值的辅助变量
k_max=5; %设定均衡算法的最大迭代次数
[Max_C_DSO,ind]=max(C_DSO); %寻找区域1中最大的上层目标函数值和对应的电价样本点集编号
y(1).S=[Max_C_DSO]; %给y(l)的S赋予当前找到的上层目标函数值
y(l).X=lambda_DA(ind,:); %给y(1)的X赋予当前找到的最优电价样本
S(ind)=[]; %将S的集合中删去此时的区域1的最优解的值
SL(ind,:)=[];
lambda_DA0=lambda_DA(ind,:); %设定区域l的中心电价的值
while 1if isempty(S) %判断S是否为非空集(也就是关键区域完成划分)break;endeval(['y',num2str(l),'.S=[];']); eval(['y',num2str(l),'.X=[];']);k=1; %设定初始迭代次数while k<=k_maxif isempty(S) %判断S是否为非空集(也就是关键区域完成划分)break;elselambda_DA_max=max(sqrt(sum(SL.^2,2))); %计算得到电价的上边界值lambda_DA_min=min(sqrt(sum(SL.^2,2))); %计算得到电价的下边界值r=norm(lambda_DA_max-lambda_DA_min)/3*(k_max-k+1)/k_max; %计算得到半径rind=Fun_R(lambda_DA0,SL,r); %寻找距离中心点小于等于r的点的编号if isempty(ind) %确认寻找到的点集非空break;elseeval(['y',num2str(l),'.S=[y',num2str(l),'.S;S(ind)];']);eval(['y',num2str(l),'.X=[y',num2str(l),'.X;SL(ind,:)];']);S(ind)=[]; %将S的集合中删去此时距离小于r的值SL(ind,:)=[]; %将SL的集合中删去此时距离小于r的值k=k+1; %均衡算法迭代次数加一endendend

3 程序结果

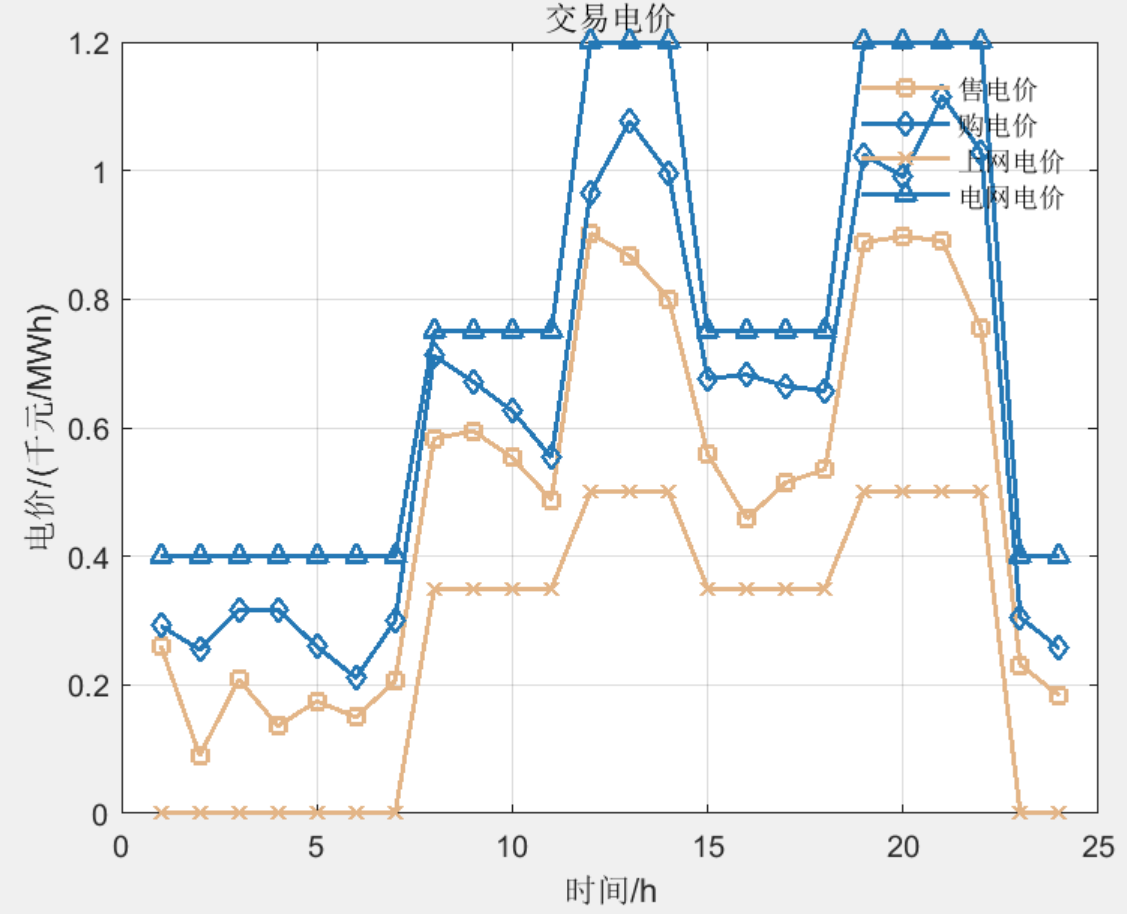
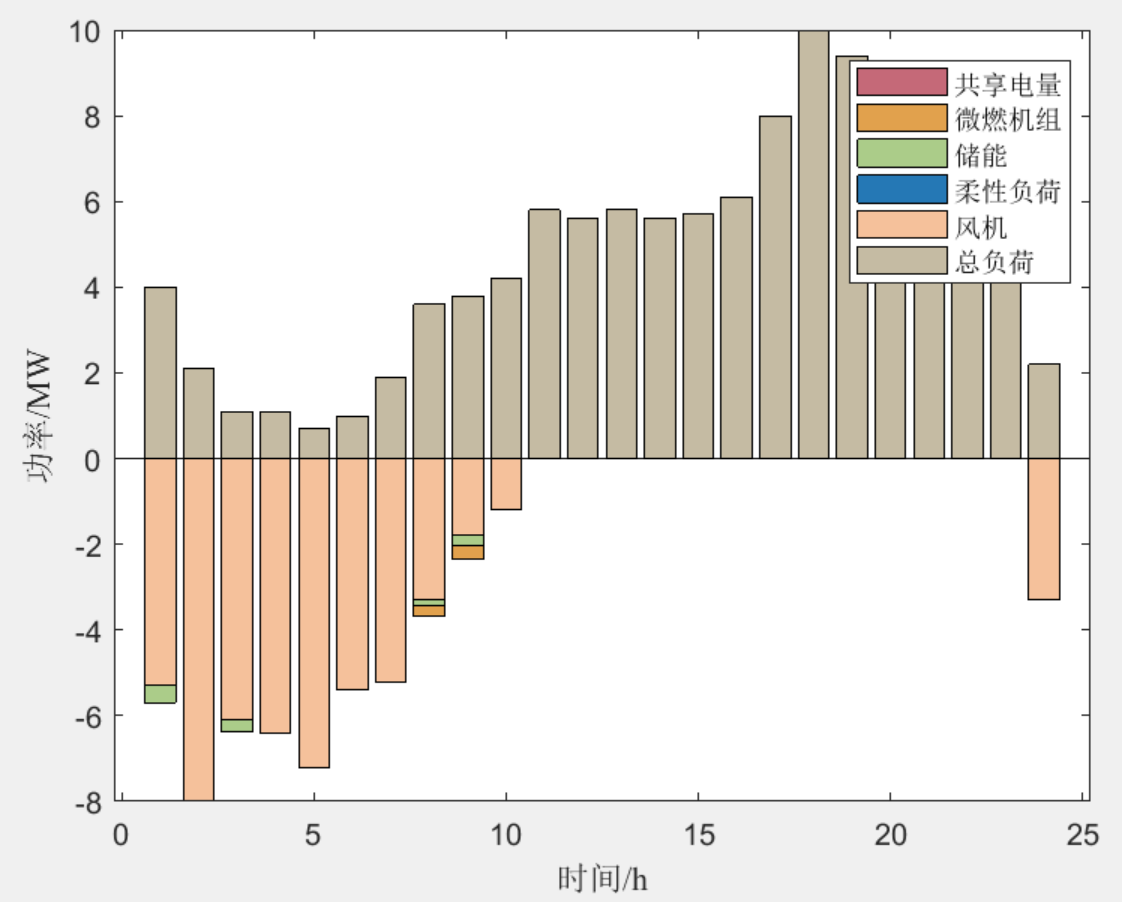
4 下载链接

基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理