Tag

【快慢指针】【哈希集合】【计数】【链表】

---

题目来源

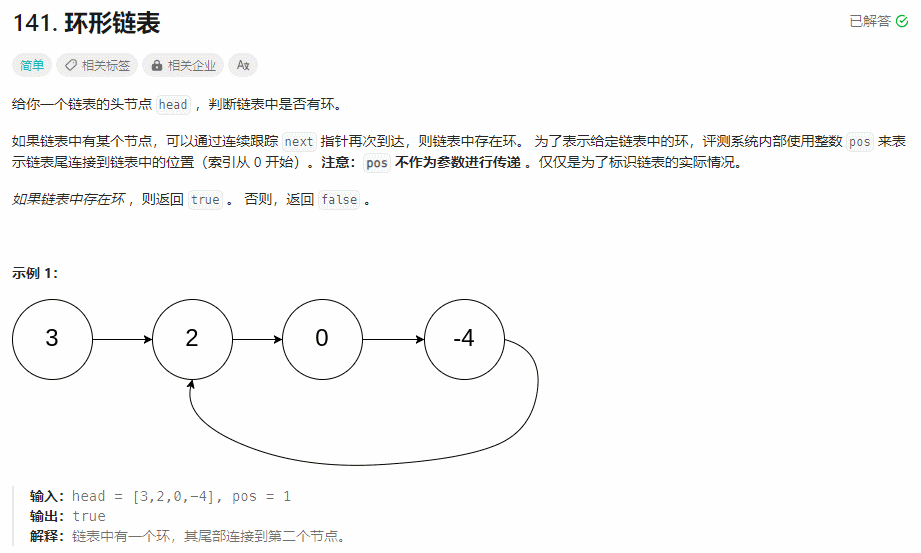
141. 环形链表

---

题目解读

判断一个链表中是否存在环。

---

解题思路

链表中有环，那么在遍历链表中节点的时候就有部分元素被重复遍历，于是可以想到使用一个集合来记录已经遍历的节点，如果集合中有节点在遍历的时候第二次出现，那么一定存在环。该方法看似可以判断环的问题，但是链表中的节点会存在重复值，在无环的链表中也可能存在某些节点值被遍历了两次，导致无环链表被误判成有环链表。

如果集合中存放的是节点而不是节点的值呢？这样就可以唯一表示每一个节点了，因为每一个节点实际上是一个结构体（c语言中）或者类（c++中），都是以地址的形式存在于栈上。

接下来将介绍三种判断链表中是否有环的方法，方法一是哈希集合的方法，方法二是一种数学上的方法，方法三是一种 “巧妙” 的方法。这三种方法都推荐大家认真学习，务必要掌握。

方法一：哈希集合

遍历链表，将经过的节点存到哈希集合中，如果集合中已经存在了该节点，就说明链表中存在环。

实现代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {unordered_set<ListNode*> st;while (head) {if (st.count(head)) {return true;}st.insert(head);head = head->next;}return false;}
};

复杂度分析

时间复杂度：$O(N)$，其中 $N$ 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。

空间复杂度：$O(N)$，其中 $N$ 是链表中的节点数。主要为哈希表的开销，最坏情况下我们需要将每个节点插入到哈希表中一次。

方法二：快慢指针

我们可以使用快慢指针来判断是否有环。定义一个慢指针 slow 每次只移动一个位置，定义一个快指针 fast 每次移动两个位置，两个指针从同一个节点出发：

• 如果链表中没有环，快指针一定会到达最后的 nullptr 节点；
• 如果链表中有环，那么两个指针一定会在环内相遇。

实现代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {if (head == nullptr || head->next == nullptr)return false;ListNode *slow = head;ListNode *fast = head->next;while (fast != slow) {if (fast == nullptr || fast->next == nullptr)return false;slow = slow->next;fast = fast->next->next;}return true;}
};

代码中的 while 循环的条件语句是 slow != fast，即快慢指针相等的时候才会退出循环。我们初始化的慢指针为 head，快指针为 head->next，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行，才会对两指针进行上述的初始化，相当于快慢指针是从 dummy head（头结点的虚构的上一个）这个节点同时出发的，我们先让快慢指针出发了各自的一个步幅，这样就可以使用 while 循环了。

当然也可以使用 do...while 循环，这样的话快慢指针初始化为 head 就可以了。

while 语句与 do...while 语句的区别在于前者是先判断再执行，而后者是先执行再判断。

复杂度分析

时间复杂度：$O(N)$，其中 $N$ 是链表中的节点数。

空间复杂度：$O(1)$。

方法三：计数

方法二就比较简单了。如果链表中存在环，那么在遍历链表的时候一定有一些节点值被重复遍历了多次。由于本题中链表最多有 $1e4$ 个节点，因此我们边遍历节点边计数（从头结点到当前节点的个数），如果数量大于 $1e4$，那么链表中一定存在环，我们直接退出迭代遍历的过程，返回 false。

实现代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {int cnt = 0;while (head) {++cnt;if (cnt > (int)1e4) {return true;}head = head->next;}return false;}
};

复杂度分析

时间复杂度：$O(N)$，其中 $N$ 是链表中的节点数。我们只有遍历每个节点一次之后才能判断出有没有环。

空间复杂度：$O(1)$。

---

拓展

本题中如果还需要求有环链表中的入环点，那么该怎么解决呢？也就是 142. 环形链表 II 这个题目要解决的问题。

最简单的方法还是哈希集合的方法，当某个节点第二次出现，该节点就是要求的入环点，该方法很简答这里不予说明。

重点来看一下如何使用 快慢指针法 来求入环点。

先来假设一些变量，入环点之前的距离为 a，入环点到快慢指针第一相遇的点的距离为 b，此时环中剩下的距离为 c，快指针在环中走了 $n$ 圈之后，快、慢指针第一次相遇，于是快慢指针行走的位置距离为：

• 慢指针：a+b；
• 快指针：a+b+n(b+c)。

慢指针每次走一个节点位置，快指针每次走两个节点位置，快指针走的路程就是慢指针的两倍，所以快慢指针行走的位置距离有这样的关系：

$$2(a+b)=a+b+n(b+c)$$

化简得到：

$$c=a+b+(b+c)(n-1)$$

根据以上公式推导可以知道，当入环点到第一次相遇点的距离加上 $n-1$ 圈的环的长度等于链表头部到入环点的距离。进一步来讲，如果两个指针分别从头结点和第一次相遇点出发，每次行进一个节点，那么它们相遇的节点（第一次相遇）就是入环点。

实现代码

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {if (head == NULL || head->next == NULL || head->next->next == NULL) {return NULL;}ListNode *slow = head->next, *fast = head->next->next;while (slow != fast) {if (fast->next == NULL || fast->next->next == NULL) {return NULL;}slow = slow->next;fast = fast->next->next;}fast = head;while (slow != fast) {slow = slow->next;fast = fast->next;}return slow;}
};

---

其他语言

python3

以下是 快慢指针法 判断链表中是否有环的python3语言代码

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = Noneclass Solution:def hasCycle(self, head: Optional[ListNode]) -> bool:if not head or not head.next:return Falseslow = headfast = head.nextwhile fast != slow:if not fast or not fast.next:return Falseslow = slow.nextfast = fast.next.nextreturn True

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 👍 哦。