概览
B树(作为B树访问方法实现)是一种数据结构,它使您能够通过从树的根向下查找树的叶节点中所需的元素。为了明确地标识搜索路径,必须对所有树元素进行排序。B树是为有序数据类型设计的,这些数据类型的值可以进行比较和排序。
下面的机场代码索引构建示意图将内部节点显示为水平矩形;叶节点垂直排列。
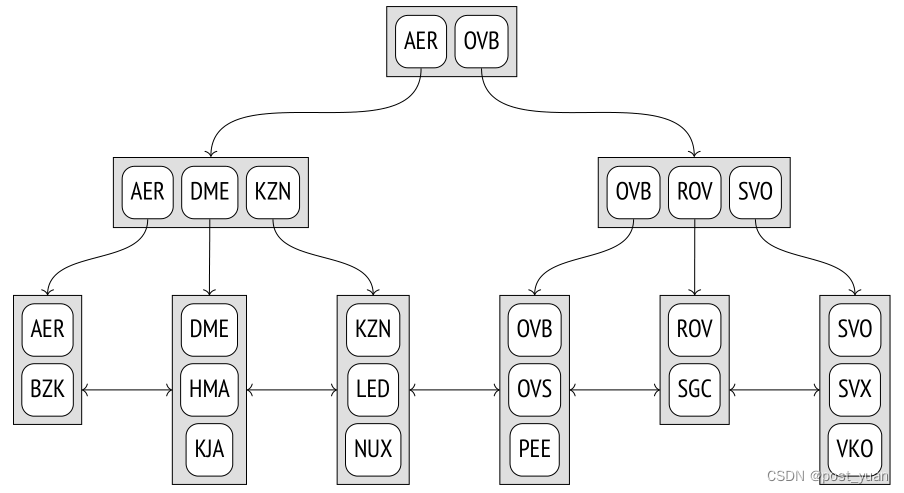
每个树节点包含几个元素,这些元素由一个索引键和一个指针组成。内部节点元素是下一层的引用节点;叶节点元素引用堆元组(图中没有显示这些引用)。
B树具有以下重要属性:
- 它们是平衡的,这意味着树的所有叶节点都位于相同的深度。因此,它们保证所有值的搜索时间相等。
- 它们有大量的分支,也就是说,每个节点包含许多元素,通常有数百个元素(为了清晰起见,该图仅显示了三个元素节点)。因此,B树深度总是很小,即使对于非常大的表也是如此。
- 索引中的数据在每个节点内以及在同一级别的所有节点上按升序或降序排序。对等节点被绑定到一个双向列表中,因此可以通过简单地以一种或另一种方式扫描列表来获得有序的数据集,而不必每次都从根开始。
搜索与插入
等值搜索
让我们看一下如何根据条件“索引-列=表达式”在树中搜索值。我们将尽力找到KJA机场。
搜索从根节点开始,访问方法必须确定要下降到哪个子节点。它选择K i键,满足K i≤表达式< K i+1。
根节点包含键AER和OVB。条件AER < KJA<OVB成立,因此我们需要下降到具有AER键的元素所引用的子节点。
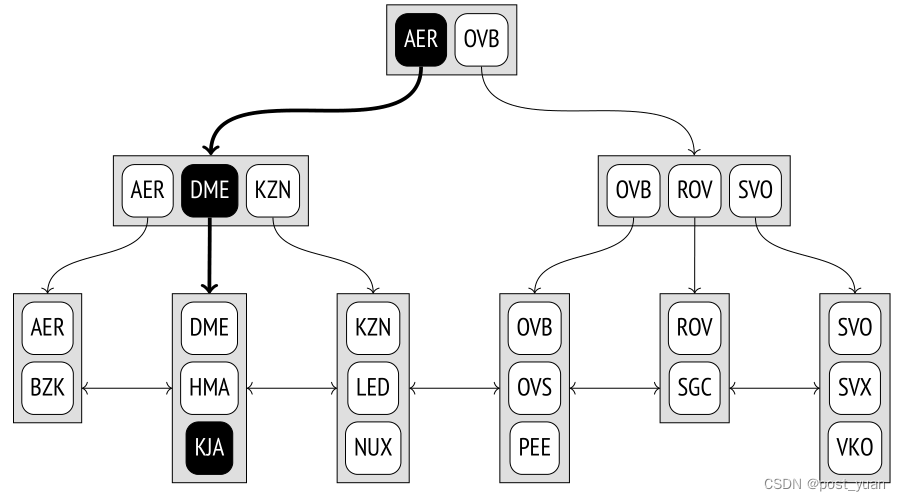
这个过程递归地重复,直到我们到达包含所需元组ID的叶节点。在这种特殊情况下,子节点满足条件DME≤KJA < KZN,因此我们必须下降到具有DME键的元素所引用的叶节点。
您可以注意到,树的内部节点中最左边的键是冗余的:要选择根的子节点,只要满足条件KJA < OVB就足够了。B树不存储这样的键,所以在下面的插图中,我将保留相应的元素为空。
叶节点中需要的元素可以通过二分查找快速找到。
然而,搜索过程并不像看起来那么简单。必须考虑到,索引中数据的排序顺序可以是升序(如上所示),也可以是降序。即使是唯一的索引也可以有几个匹配的值,并且必须返回所有这些值。此外,可能有太多的副本,以至于它们不适合单个节点,因此相邻的叶节点也必须处理。
最重要的是,当搜索正在进行时,其他进程可能会修改数据,页面可能被分成两个,树结构可能会发生变化。所有的算法都被设计为尽可能减少这些并发操作之间的争用,并避免过多的锁,但是我们在这里不打算讨论这些技术细节。
不等值搜索
如果搜索是通过条件“索引-列 ⩽expression”(或“索引-列⩾expression”)执行的,我们必须首先搜索满足相等条件的值的索引,然后在所需的方向遍历其叶节点,直到到达树的末端。
该图说明了搜索小于或等于DME的机场代码。
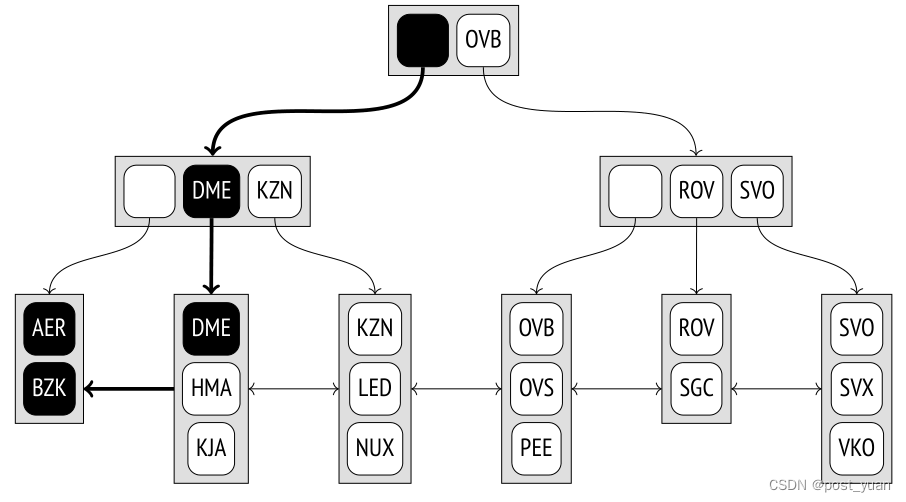
对于小于和大于操作符,过程相同,只是必须排除第一个找到的值。
范围搜索
当按照“表达式1≤索引列≤表达式2”的范围进行搜索时,我们必须先找到表达式1,然后沿着正确的方向遍历叶节点,直到找到表达式2。该图说明了在LED和ROV之间的范围内搜索机场代码的过程。
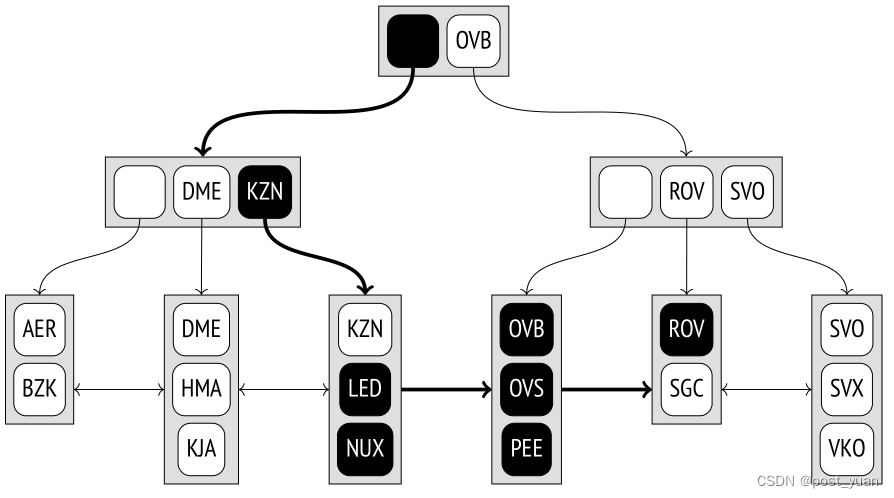
插入
新元素的插入位置由键的顺序明确定义。例如,如果将RTW机场代码插入到表中,则新元素将出现在ROV和SGC之间的最后一个叶节点中。
但是如果叶节点没有足够的空间容纳新元素怎么办?例如(假设一个节点最多可以容纳三个元素),如果我们插入TJM机场代码,最后一个叶节点将被过度填充。在这种情况下,节点被分成两个,旧节点的一些元素被移动到新节点中,指向新子节点的指针被添加到父节点中。显然,父节点也可能会被填满。然后它也被分成两个节点,以此类推。如果要拆分根,则在生成的节点之上再创建一个节点,以成为树的新根。在这种情况下,树的深度增加了一级。
在本例中,TJM机场的插入导致两个节点分裂;生成的新节点在下面的图中突出显示。为了确保可以拆分任何节点,双向列表绑定了所有级别的节点,而不仅仅是最低级别的节点。
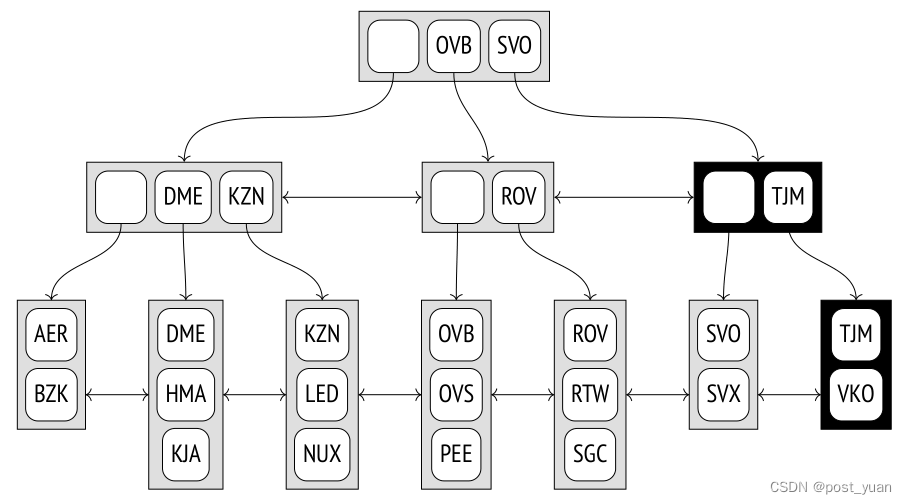
所描述的插入和分割过程保证树保持平衡,并且由于节点可以容纳的元素数量通常相当大,因此树的深度很少增加。
问题是,一旦分裂,节点就永远无法合并在一起,即使它们在垃圾回收后包含的元素非常少。这个限制并不适用于B树数据结构本身,而是适用于它的PostgreSQL实现。因此,如果在尝试插入时发现节点已满,则访问方法首先尝试删除冗余数据,以便清除一些空间并避免额外的分割。
页面布局
B树的每个节点占用一个页面。页的大小定义了节点的容量。
由于页面分割,树的根可以由不同时间的不同页面表示。但是搜索算法必须总是从根开始扫描。它在**零索引页(称为元页)**中查找当前根页的ID。元页面还包含一些其他元数据。
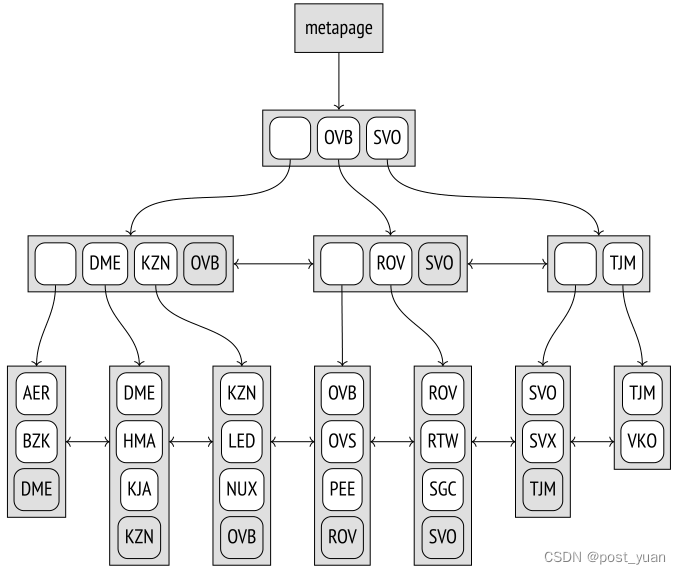
索引页中的数据布局与我们目前看到的略有不同。除了每个级别最右边的页面外,所有页面都包含一个额外的 “高键”,该键保证不小于该页中的任何键 。在上面的图表中,高音键被突出显示。
让我们使用pageinspect扩展来查看基于六位数预订引用的真实索引的页面。元页面列出根页面ID和树的深度(级别编号从叶节点开始,从零开始):

存储在索引项中的键被显示为字节序列,这不是很方便:
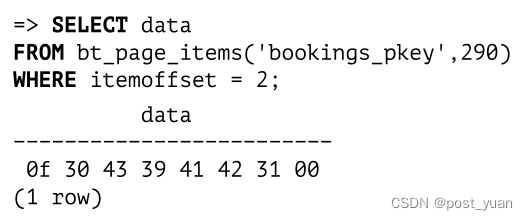
为了破译这些值,我们必须编写一个专门的函数。它不会支持所有平台,也可能不适用于某些特定场景,但它可以用于本章的示例:

现在我们可以看一下根页面的内容:

正如我所说的,第一个条目不包含键。ctid列提供到子页面的链接。
假设我们正在寻找预订E2D725。在这种情况下,我们必须选择条目19(因为E2CB14≥E2D725 < EF6FEA)并向下到第5135页。

本页中的第一个条目包含高键,这可能看起来有点出乎意料。从逻辑上讲,它应该放在页面的末尾,但从实现的角度来看,将它放在页面的开头更方便,以避免每次页面内容更改时都移动它。
在这里,我们选择条目3(因为E2D71D ⩽ E2D725 < E2E2F4),并向下到第11919页。
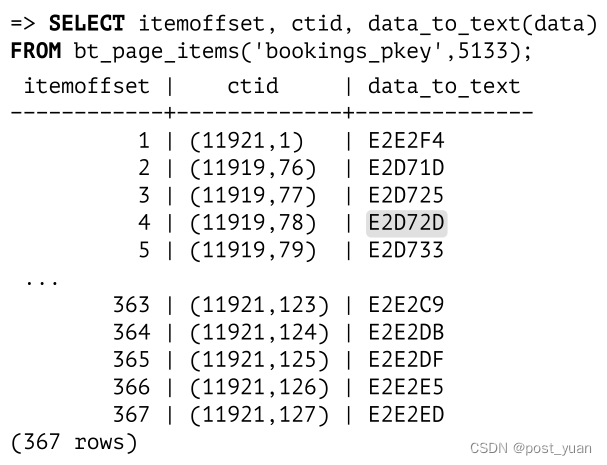
它是索引的叶子页。第一个入口是高键;所有其他条目都指向堆元组。
这是我们的预订单:

当我们按代码搜索预订时,低级别的情况大致就是这样:

重复数据删除
非唯一索引可以包含许多指向不同堆元组的重复键。由于非唯一键出现不止一次,因此占用大量空间,因此重复项被折叠成单个索引项,其中包含键和相应的元组ID列表。在某些情况下,这个过程(称为重复数据删除)可以显著减小索引大小。
但是,由于MVCC,唯一索引也可以包含重复项:索引保留对表行所有版本的引用。HOT更新机制可以帮助您避免由于引用过时的、通常寿命较短的行版本而导致的索引膨胀,但有时它可能不适用。在这种情况下,重复数据删除可以为清理冗余堆元组和避免额外的页面分割赢得一些时间。
为了避免在没有直接好处的情况下在重复数据删除上浪费资源,只有在叶子页没有足够的空间容纳另一个元组时才执行折叠。然后,页面修剪和重复数据删除可以释放一些空间,并防止不希望的页面分割。但是,如果副本很少,则可以通过关闭deduplicate_items storage参数来禁用重复数据删除特性。
部分索引不支持重复数据删除功能。主要的限制是键的相等性必须通过对其内部表示的简单二进制比较来检查。到目前为止,并不是所有的数据类型都可以用这种方式进行比较。例如,浮点数(浮点数和双精度数)对零有两种不同的表示。任意精度的数字(数字)可以用不同的尺度表示同一个数字,而jsonb类型可以使用这样的数字。如果使用非确定性排序,则不可能对文本类型进行重复数据删除,非确定性排序允许用不同的字节序列表示相同的符号(标准排序是确定性的)。
此外,复合类型、范围和数组以及用INCLUDE子句声明的索引目前不支持重复数据删除。
要检查特定索引是否可以使用重复数据删除,您可以查看其元页面中的allequalimage字段:

此时支持重复数据删除功能。事实上,我们可以看到,其中一个叶页包含具有单个元组ID (htid)和具有ID列表(tids)的索引条目:
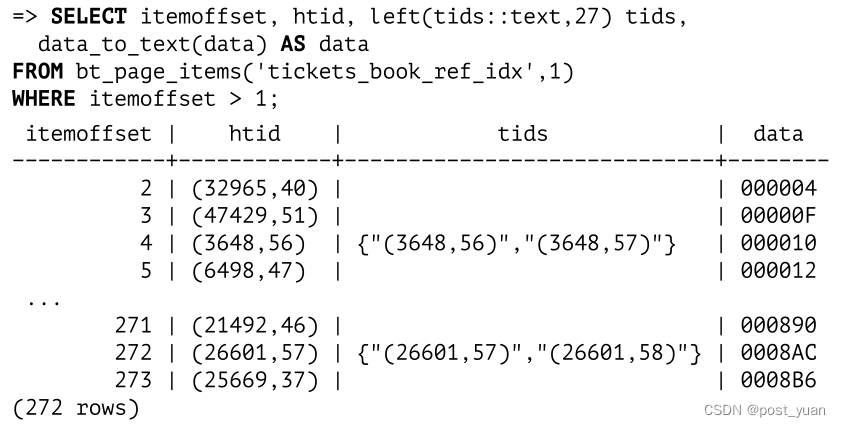
内部索引项的紧凑存储
重复数据删除可以在索引的叶页中容纳更多条目。但是,即使叶页构成了索引的大部分,在内部页中执行数据压缩以防止额外的分割也同样重要,因为搜索效率直接依赖于树的深度。
内部索引项包含索引键,但它们的值仅用于在搜索期间确定要下降到的子树。在多列索引中,通常使用第一个键属性(或几个第一个键属性)就足够了。可以截断其他属性以节省页面中的空间。
这样的后缀截断发生在叶页被分割并且内页必须容纳一个新指针的时候。
例如,下面是在包含订票参考和乘客姓名的列上建立的票务表索引的根页的几个条目:
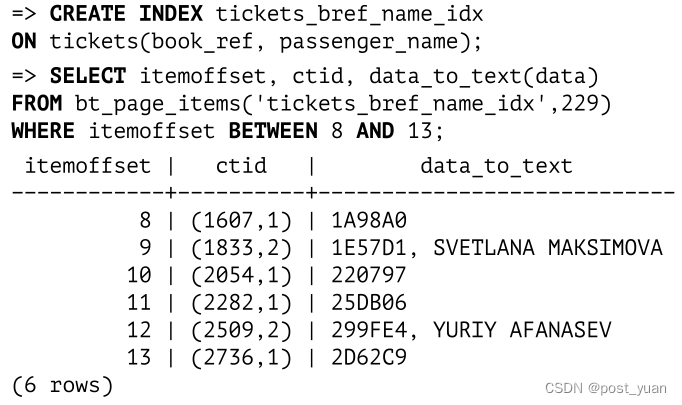
我们可以看到一些索引条目没有第二个属性。
当然,叶页必须保留所有键属性和INCLUDE列值(如果有的话)。否则,将无法执行仅索引扫描。唯一的例外是高键;它们可以部分保存。





 批量图片下载器)

--- Python和Pytorch,Tensorflow的版本对应)
)



)

-开发bug总结5)




