🔆 文章首发于我的个人博客：欢迎大佬们来逛逛
🔆 OpenCV项目地址及源代码：点击这里
文章目录
- 图像模糊操作
- 均值滤波
- 高斯滤波
- 中值滤波
- 双边滤波
图像模糊操作
关于图片的噪声：指的是图片中存在的不必要或者多余的干扰数据。
Smooth与Blur是图像处理中最简单和常用的操作之一。
经过这两种操作我们便可以实现消除噪声的作用。
Smooth与Blur操作原理是数学的卷积运算，根据不同卷积运算公式，划分了多种图像滤波方式图像滤波：指的是在尽量保留图像特征的条件下对目标图像得噪声进行抑制。
均值滤波
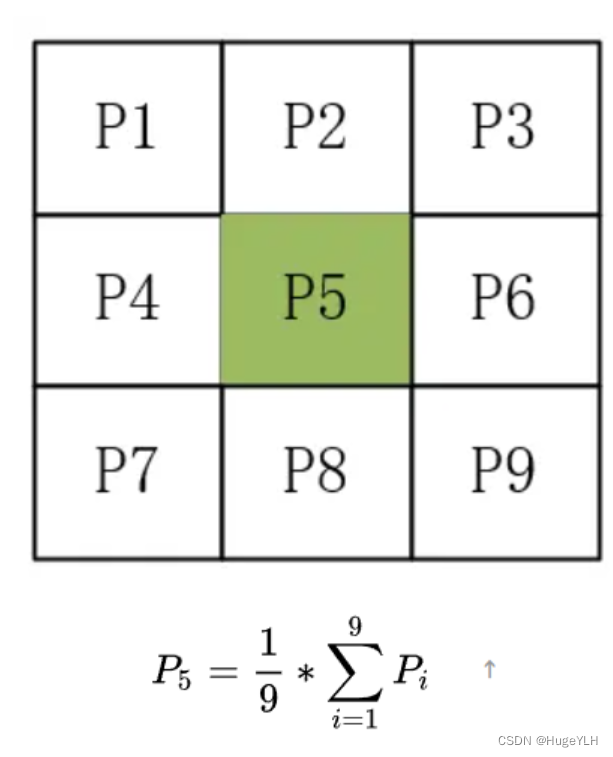
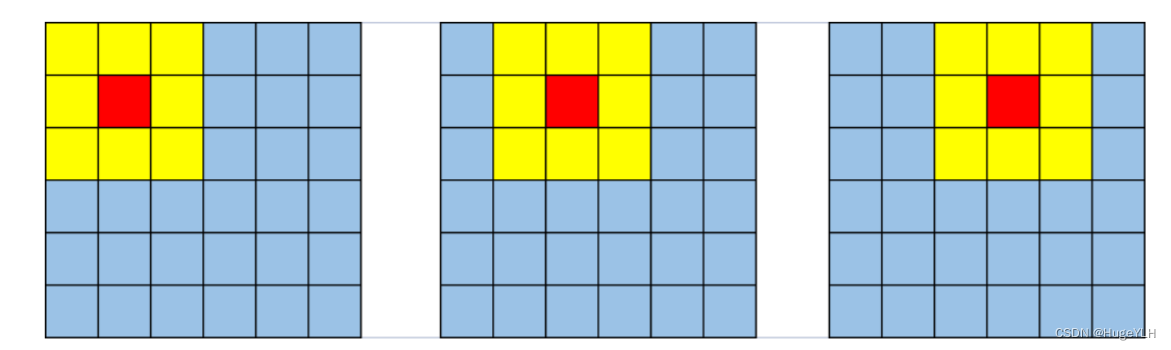
均值滤波指的是取周围像素计算出来的平均值然后赋给目标像素。然后依次对每一个像素值进行如上的操作。
均值滤波可以帮助消除图像尖锐噪声，实现图像平滑，模糊等功能。
blur可以实现均值滤波。
void blur( InputArray src, OutputArray dst,Size ksize, Point anchor = Point(-1,-1),int borderType = BORDER_DEFAULT );
/*******************************************************************
* src： 输入图像
* dst： 输出图像
* ksize： 内核大小 如上我们的大小是（3，3）
* anchor: 锚点
* 默认Point(-1,-1):锚点在核中心
* borderType: 外部像素边界模式(一般不管)
*********************************************************************/
//均值模糊void testBlur() {cv::blur(mt, saves["blur"], cv::Size(KERNEL, KERNEL));}
高斯滤波
高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。
高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
一阶与二阶高斯分布，其中二阶高斯分布是一个是一个三维的正态分布的图像：
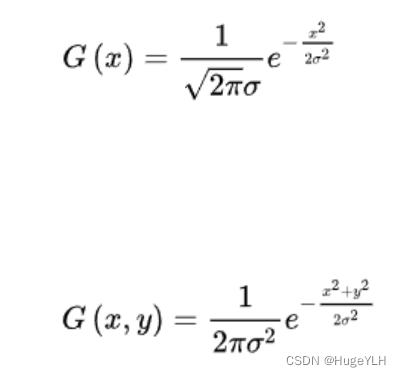
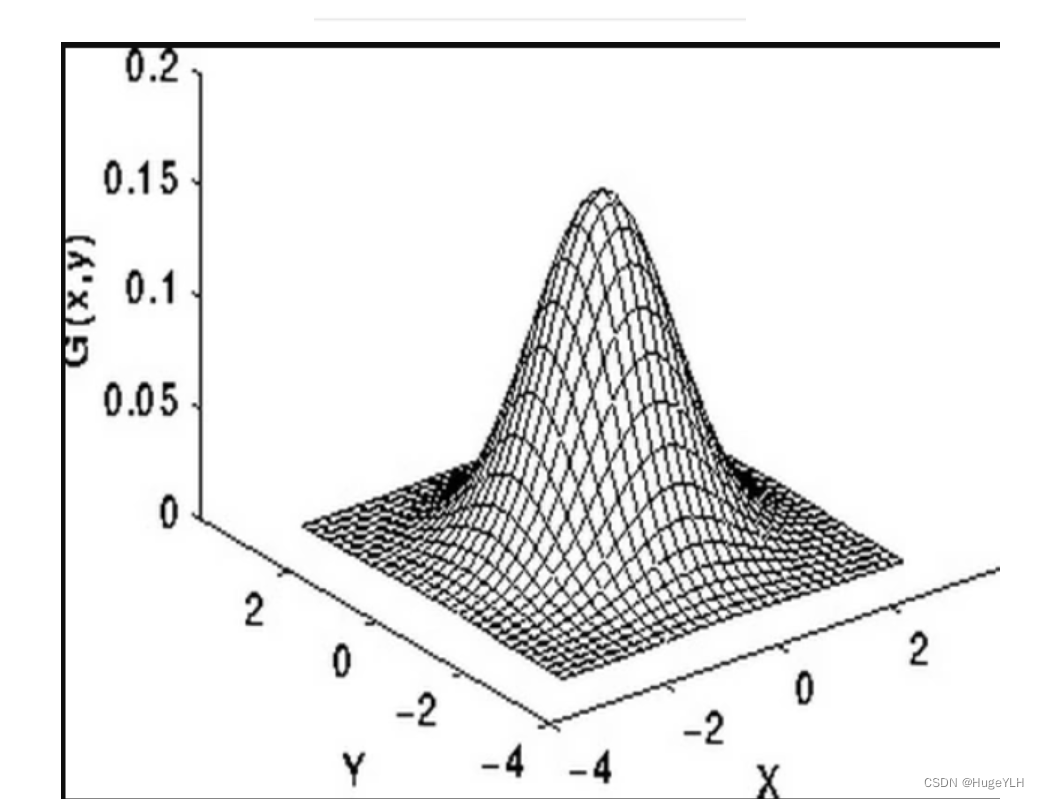
可以观察到正态分布是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。
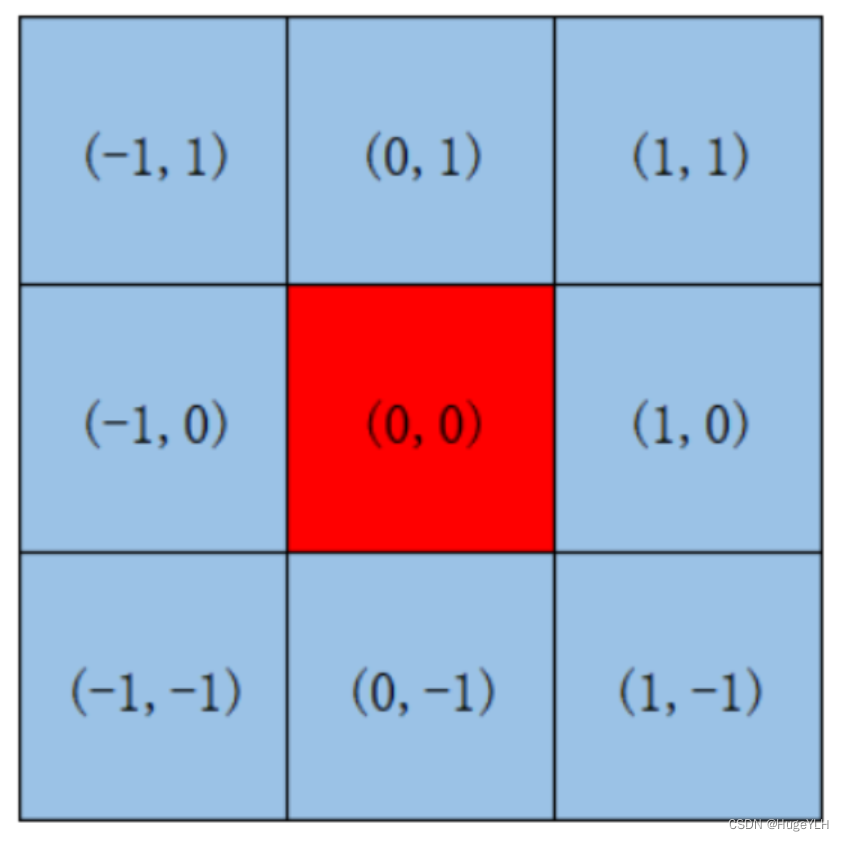
使用二阶高斯分布来消除噪声，模拟计算操作，其中 x x x 与 y y y 指的是图像的坐标，由于 σ \sigma σ 未知，并且其他都是已知的，我们便可以计算出每一个点对应的二阶高斯值。
- 取一个 σ \sigma σ 值，对于每一个位置计算出对应的二阶高斯值。
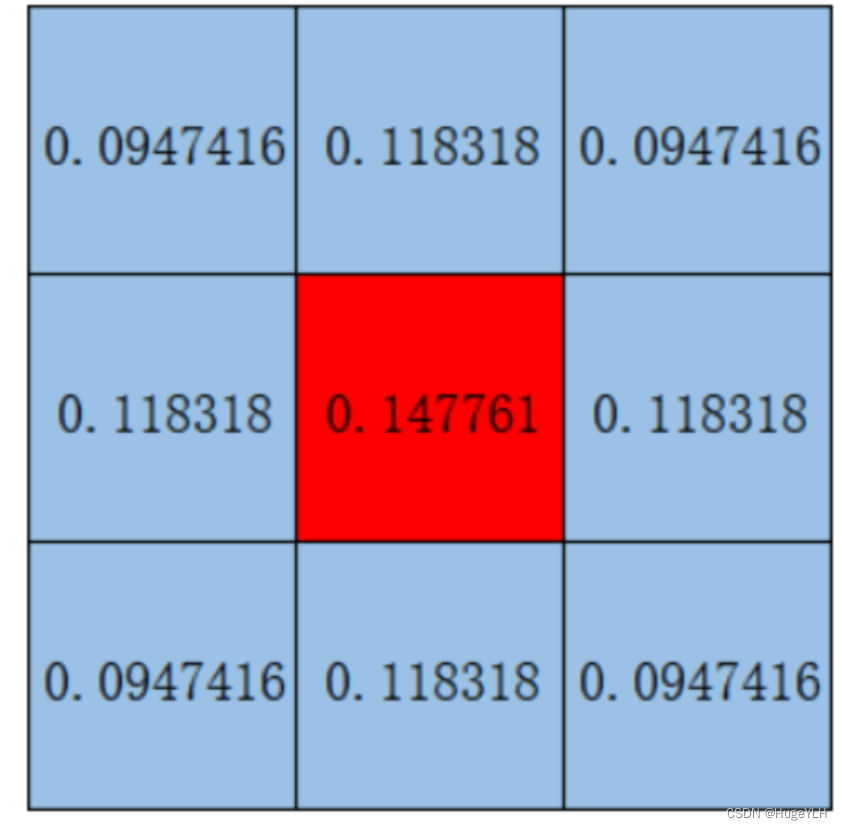
- 计算出权重总和 s u m sum sum，由于权重之和必须等于1，因此每个点再除以 s u m sum sum ，就可以得到最终的权值矩阵（右三）
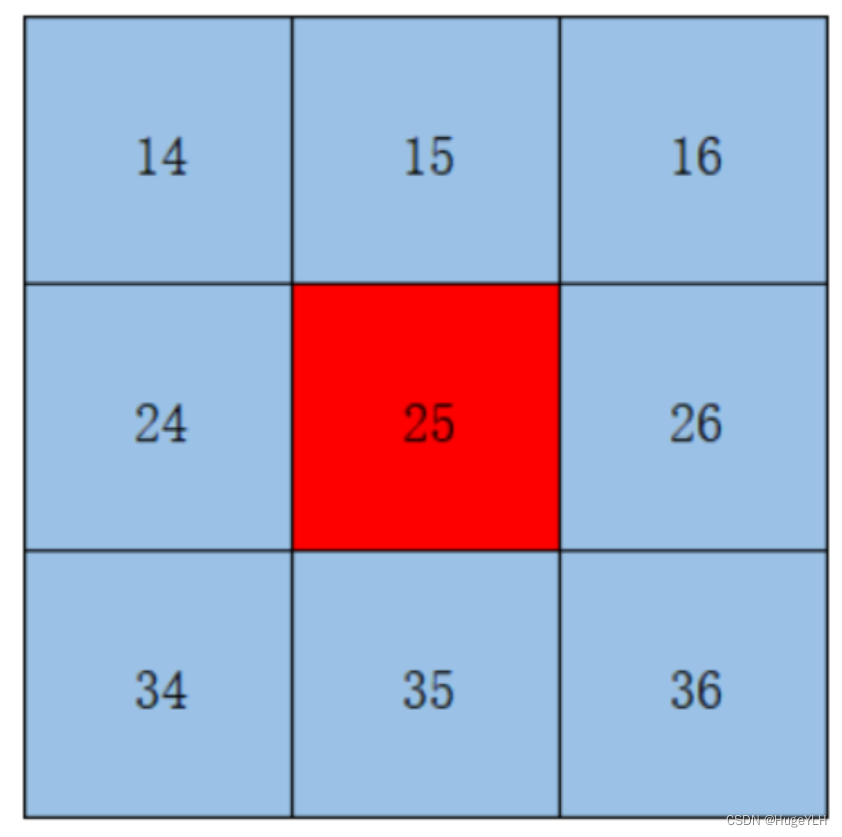
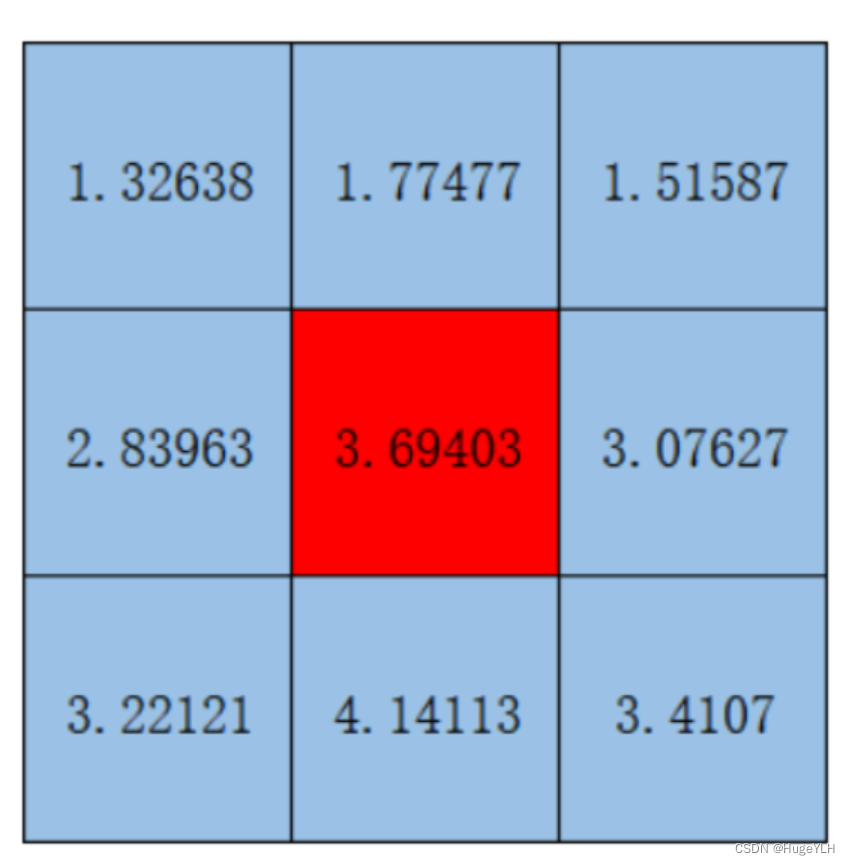
- 对于每一个位置的像素值（右二）乘以对应的权值就可以得到高斯模糊后的值（右一）。
高斯模糊函数：GaussianBlur
void GaussianBlur( InputArray src, OutputArray dst, Size ksize,double sigmaX, double sigmaY = 0,int borderType = BORDER_DEFAULT );
/*******************************************************************
* src： 输入图像
* dst： 输出图像
* ksize： 内核大小
* x,y必须是整数，并且为奇数
* sigmaX: X方向滤波系数
* sigmaY: Y方向滤波系数
* borderType: 外部像素边界模式(一般不管)
*********************************************************************/
案例代码：
//高斯模糊void testGaussianBlur() {cv::GaussianBlur(mt, saves["GaussianBlur"], cv::Size(KERNEL, KERNEL), 3, 3);}
可以观察到高斯模糊的效果比均值模糊的效果好。
中值滤波
中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。
g = median [ ( x − 1 , y − 1 ) + f ( x , y − 1 ) + f ( x + 1 , y − 1 ) + f ( x − 1 , y ) + f ( x , y ) + f ( x + 1 , y ) + f ( x − 1 , y + 1 ) + f ( x , y + 1 ) + f ( x + 1 , y + 1 ) ] g=\operatorname{median}[(x-1, y-1)+f(x, y-1)+f(x+1, y-1)+f(x-1, y)+f(x, y)+f(x+1, y)+f(x-1, y+1)+f(x, y+1)+f(x+1, y+1)] g=median[(x−1,y−1)+f(x,y−1)+f(x+1,y−1)+f(x−1,y)+f(x,y)+f(x+1,y)+f(x−1,y+1)+f(x,y+1)+f(x+1,y+1)]
对对椒盐噪声有很好的抑制作用.
它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）
API：medianBlur
void medianBlur( InputArray src, OutputArray dst, int ksize );
/*******************************************************************
* src： 输入图像
* dst： 输出图像
* ksize： 内核大小
* 大小必须是大于1而且必须是奇数
*********************************************************************/
//中值模糊
void testMedianBlur() {cv::medianBlur(mt, saves["median"], KERNEL);
}
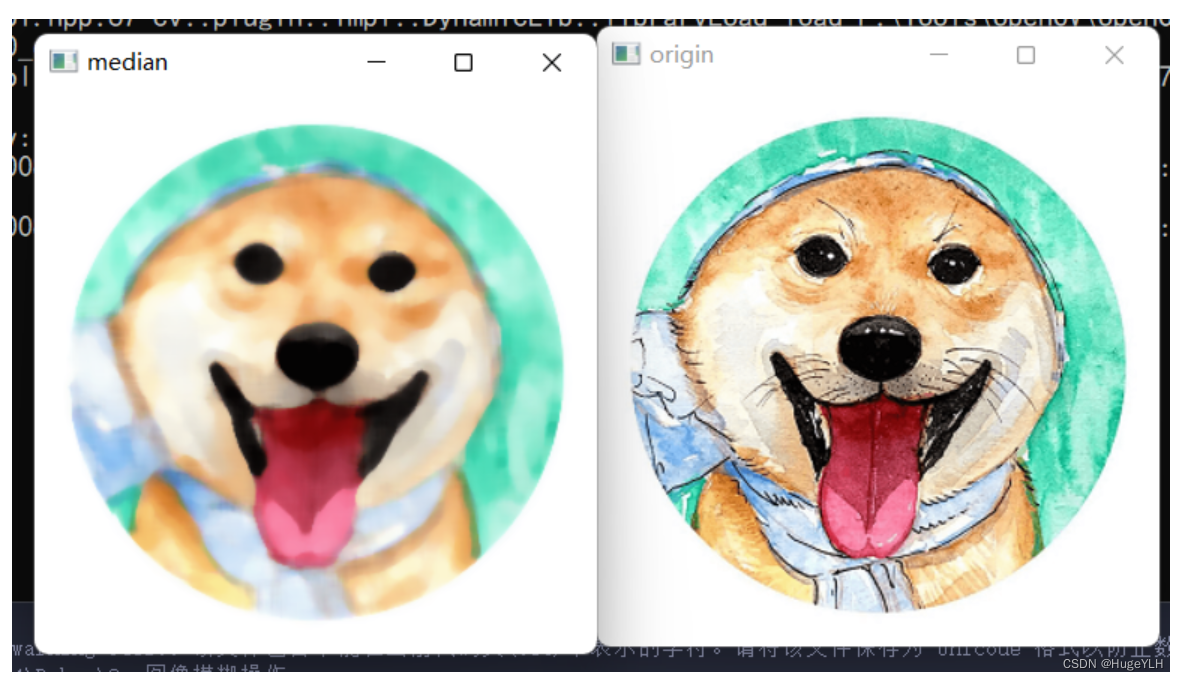
双边滤波
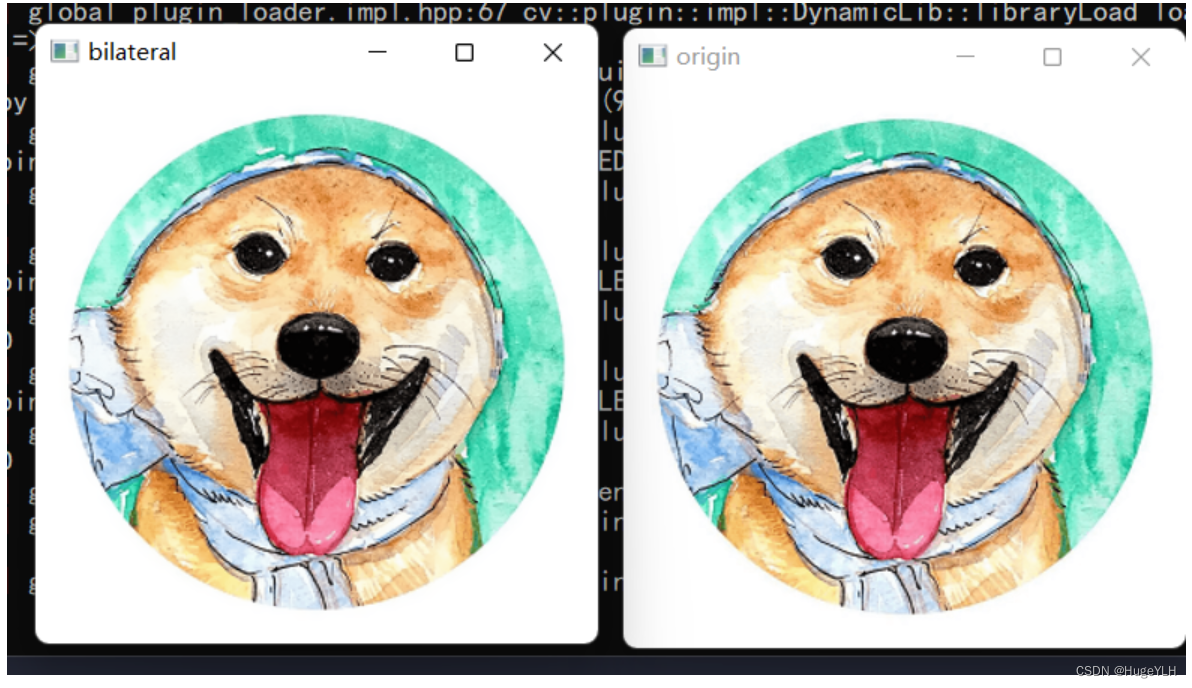
上面三种降噪方法容易模糊图片的边缘细节，对于高频细节的保护效果并不明显。
双边滤波可以很好的边缘保护，即可以在去噪的同时，保护图像的边缘特性。
w ( i , j , k , l ) = exp ( − ( i − k ) 2 + ( j − l ) 2 2 σ d 2 − ∥ f ( i , j ) − f ( k , l ) ∥ 2 2 σ r 2 ) w(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right) w(i,j,k,l)=exp(−2σd2(i−k)2+(j−l)2−2σr2∥f(i,j)−f(k,l)∥2)
函数API：bilateralFilter
void bilateralFilter( InputArray src, OutputArray dst, int d,double sigmaColor, double sigmaSpace,int borderType = BORDER_DEFAULT );
/*******************************************************************
* src： 输入图像
* dst： 输出图像
* d： 滤波过程中每个像素邻域的直径
* sigmaColor: 颜色空间滤波器的标准差值
* 参数越大表明该像素领域内有越多的颜色被混合到一起
* sigmaSpace: 空间间坐标中滤波器的标准差值
* borderType: 外部像素边界模式(一般不管)
*********************************************************************/
void testBilateralFilter() {cv::bilateralFilter(mt, saves["bilateral"], KERNEL, KERNEL, KERNEL);}
参考：
bilateral filter双边滤波器的通俗理解_AI吃大瓜的博客-CSDN博客
均值滤波
高斯滤波_百度百科
