一、原因
原因很简单,计算机存储和计算数组都是用二进制,
而大部分小数转二进制的时候,就丢失精度了。
0.1、0.2、0.3这些小数在二进制里都是循环小数,计算机不可能存储无限循环小数,所以只能截取一部分,导致本身失去精度。
计算机再用这些有误差的小数进行计算,那误差就更大了。
互转教程:十进制小数 与 二进制小数 互转
二、一分钱问题
假如用float和double进行金钱计算,因为二进制转换误差就很容易出现一分钱问题。
方案
方案1、 使用BigDecimal
BigDecimal a = new BigDecimal("0.1"); //切记!!参数一定要是字符串
BigDecimal b = new BigDecimal("0.2"); //切记!!参数一定要是字符串
BigDecimal c = a.add(b);
System.out.println(c);
切记!!
创建BigDecimal参数一定要是字符串。
如果直接传参浮点数,计算机自动转二进制,同样会有误差!!!
方案2、 使用long
1、金钱保存到数据库时,金钱乘1000,字段类型为整型。
2、计算时就使用整型计算。
3、显示时金钱/1000。
long a = 0.1 * 1000;
long b = 0.2 * 1000;
long c = a + b;
System.out.println(c / 1000);
三、扩展知识 IEEE-754二进制
计算机浮点数标准。
它规定了浮点数的表示、运算和舍入方式等方面的规则。
1、IEEE-754二进制组成
| 类型 | 符号位 | 阶码 | 尾数 |
|---|---|---|---|
| float | 占1bit | 占8bit | 占23bit |
| double | 占1bit | 占11bit | 占52bit |
- 符号位,0表示正数,1表示负数。
- 指数,浮点数的大小和符号的指数部分。127偏移量
- 尾数,浮点数的小数部分。
2、十进制float转IEEE-754二进制
| 步骤 | 例子0.5 | 例子-12 | |
|---|---|---|---|
| 1 | 获取【符号位】 0表示正数,1表示负数。 | 0.5是正数,符号位为0 | -12是负数,符号位为1 |
| 2 | 十进制小数 转 二进制 | 十进制0.5转二进制 0.1 | 十进制-12转二进制 1100.011 |
| 3 | 二进制转科学计数法 1.xx * 2 指数 2^{指数} 2指数 | 1.0 ∗ 2 − 1 1.0 * 2^{-1} 1.0∗2−1 | 1.100011 ∗ 2 3 1.100011 * 2^3 1.100011∗23 |
| 4 | 获取十进制指数值 127+指数 | 127+(-1)=126 | 127 + 3 = 130 |
| 5 | 【指数值】 十进制 转 二进制 不满八位前面补0 | 126 ->01111110 | 130 -> 10000010 |
| 6 | 【尾数位】 科学计数法的 xx 不满23位后面补0 | xx为0 补零:00000000 00000000 0000000 | xx为100011 补零:10001100 00000000 0000000 |
| 7 | 拼接 符号位+指数值+尾数位 | 0 10000010 00000000000000000000000 | 1 10000010 10001100000000000000000 |
我们再用上面步骤计算float 0.1。
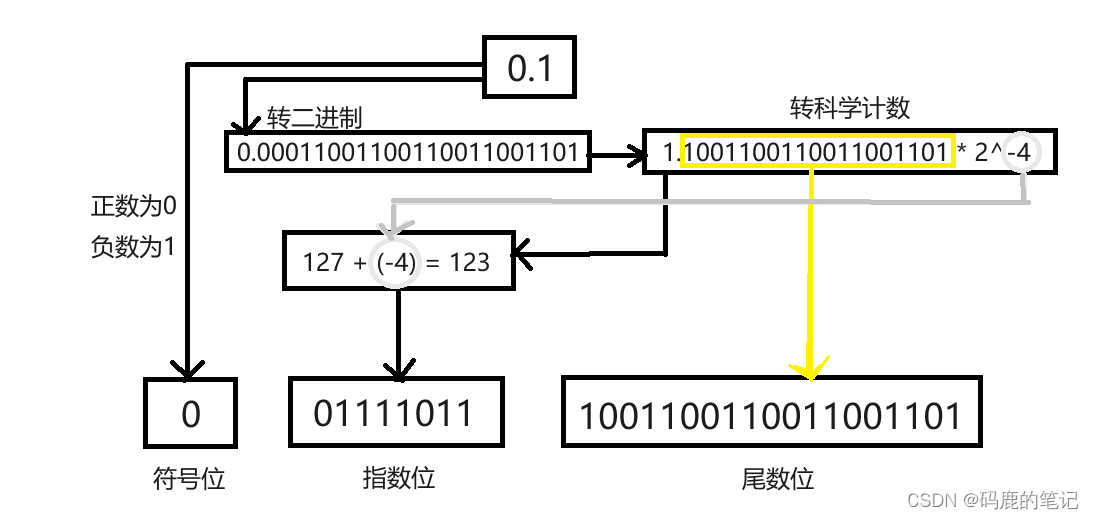
- 0.1获取符号位,0.1正数为0。
- 0.1转二进制,0.00011001100110011001101(已失去精度)
- 科学计数法, 1.1001100110011001101 ∗ 2 − 4 1.1001100110011001101 * 2^{-4} 1.1001100110011001101∗2−4
- 获取十进制指数值,127 + (-4) = 123
- 指数值 转 二进制,123 -> 01111011
- 尾数位补零,10011001 10011001 101
- IEEE-754二进制:0 01111011 1001100110011001101






![[Machine Learning][Part 6]Cost Function代价函数和梯度正则化](http://pic.xiahunao.cn/[Machine Learning][Part 6]Cost Function代价函数和梯度正则化)





![2023年中国清净剂行业需求现状及前景分析[图]](http://pic.xiahunao.cn/2023年中国清净剂行业需求现状及前景分析[图])

)




