6.4 图的存储结构

思维导图：

前言：

---

**6.4 图的存储结构**

- **核心问题**：由于图的结构复杂性，我们不能仅仅依赖于元素在存储区的物理位置来表示它们之间的关系。

- **邻接矩阵**：
- **基本思路**：虽然图没有顺序存储结构，但我们可以用二维数组来模拟元素之间的关系。
- **适用情境**：当你需要快速判断两个顶点之间是否存在边时。

- **链式存储**：
- **基本思路**：由于图中任意两点可能都有关系，使用链式存储是很自然的选择。
- **种类**：
- 邻接表：适合于表示稀疏图。
- 十字链表：适合于有向图。
- 邻接多重表：适合于既有边又有弧的图。
- **选择依据**：根据实际应用和需要来选择最适合的链式存储结构。

---

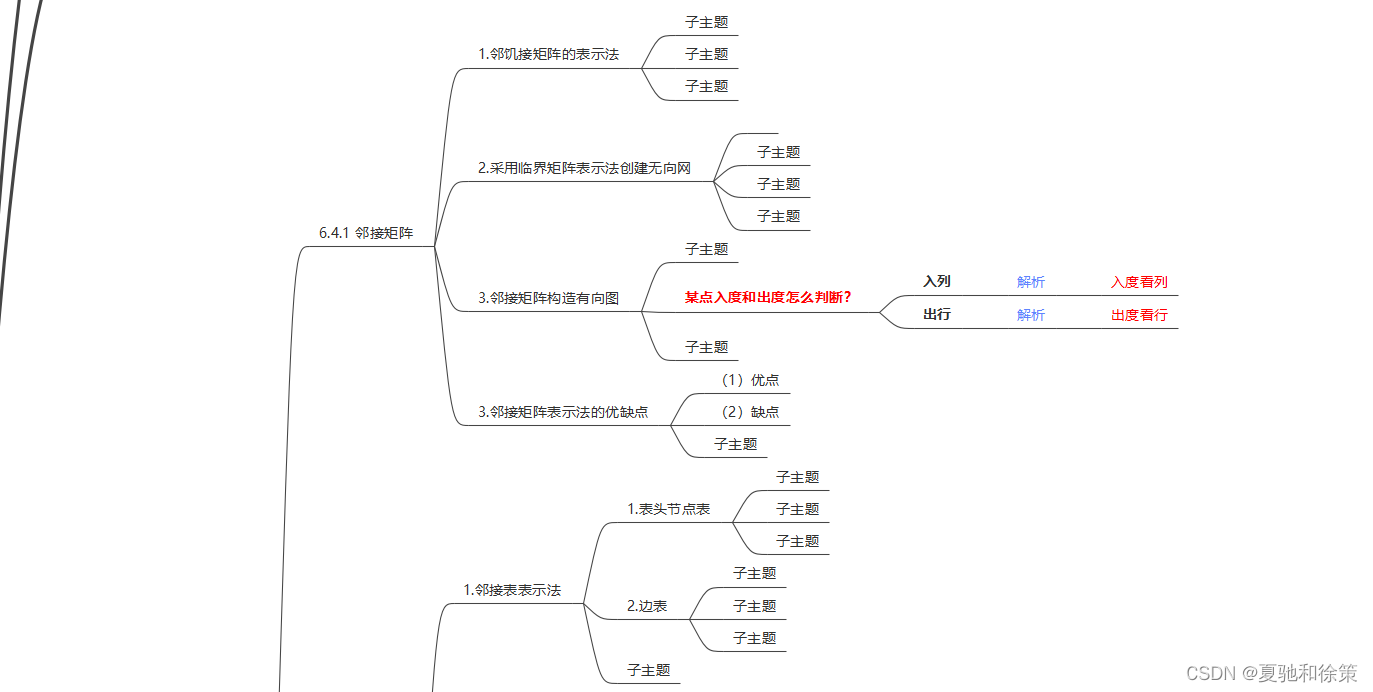
6.4.1 邻接矩阵

**1. 概述**
邻接矩阵是用于表示图中顶点之间关系的矩阵。对于一个含有n个顶点的图，其邻接矩阵是一个n阶方阵。该矩阵能够表示顶点之间是否存在边，以及边的权值。

**2. 创建无向网的邻接矩阵**

**算法6.1：采用邻接矩阵表示法创建无向网**

- **步骤：**
1. 输入总顶点数和总边数。
2. 依次输入点的信息并保存到顶点表中。
3. 初始化邻接矩阵，将每个权值设置为极大值。
4. 构建邻接矩阵。输入每条边的顶点和其权值，然后在图中确定两个顶点的位置，赋予边相应的权值，并使其对称边具有相同的权值。

- **算法描述：**
1. 输入总顶点数和总边数。
2. 输入每个顶点的信息。
3. 初始化邻接矩阵的权值为极大值。
4. 构建邻接矩阵：输入边的顶点和权值，然后确定顶点在图中的位置，并设置边的权值。

**3. 邻接矩阵的优缺点**

- **优点：**
1. 可以轻松判断两个顶点之间是否存在边。
2. 方便计算每个顶点的度。

- **缺点：**
1. 增加和删除顶点不方便。
2. 统计边的数量不便，因为需要检查所有邻接矩阵的元素，时间复杂度为O(n²)。
3. 空间复杂度高。对于有n个顶点的有向图，需要n²个单元来存储边。对于无向图，由于邻接矩阵是对称的，可以使用压缩存储的方式。

6.4.2 邻接表

### 定义：
邻接表(Adjacency List)是图的一种链式存储结构。

### 结构：
1. **表头节点表**:
- 表示方式: 由所有表头节点以顺序结构的形式存储，便于随机访问任一顶点的边链表。
- 包含：数据域(data)和链域(firstarc)。
- 数据域: 用于存储顶点v的名称或其他相关信息。
- 链域: 指向链表中第一个节点(与顶点v邻接的第一个邻接点)。
- 示意图：图6.11(a)展示了表头节点的结构。

2. **边表**:
- 表示方式: 由表示图中顶点间关系的2n个边链表组成。
- 包含：邻接点域(adjvex)、数据域(info)和链域(nextarc)。
- 邻接点域: 指示与顶点v邻接的点在图中的位置。
- 数据域: 存储和边相关的信息，如权值等。
- 链域: 指示与顶点v邻接的下一条边的节点。
- 示意图：图6.11(b)展示了边节点的结构。

### 特点：
- 对于每个顶点v，建立一个单链表，其中列出与v相邻接的所有顶点。
- 在无向图的邻接表中，顶点v的度是第i个链表中的节点个数。
- 在有向图中，第i个链表中的节点个数是顶点v的出度。为计算入度，必须遍历整个邻接表。邻接点域的值为i的节点个数表示顶点v的入度。
- 有时，为了确定顶点的入度，可以创建一个有向图的逆邻接表。逆邻接表是针对每个顶点v，建立一个链表，该链表连接所有进入v的边。

### 逆邻接表：
- 定义：对于每个顶点v，逆邻接表建立一个链表，该链表连接所有进入v的边。
- 用途：方便地确定顶点的入度，而不需要遍历整个邻接表。
- 示意图：图6.12(c)展示了有向图G的逆邻接表。

### 示例：
- 如图6.12(a)所示，这是图6.1中G₁的邻接表。
- 如图6.12(b)所示，这是图6.1中G₂的邻接表。
- 如图6.12(c)所示，这是有向图G的逆邻接表。

### 小结：
邻接表是图的一种有效的链式存储结构，尤其适合于稀疏图。表头节点表存储顶点的信息，而边表存储与特定顶点相邻接的所有顶点。对于有向图，除了邻接表外，还可以构建逆邻接表来便于确定顶点的入度。

笔记：图的邻接表存储结构及优缺点

### 图的邻接表存储结构：

1. **定义**：邻接表是图的一种链式存储结构。其中包括顶点的头节点和表示边的边节点。

2. **组成**：
- **顶点信息 (VNode)**：
- data: 存放顶点数据。
- firstarc: 指向第一条依附该顶点的边的指针。
- **边节点 (ArcNode)**：
- adjvex: 该边所指向的顶点的位置。
- nextarc: 指向下一条边的指针。
- info: 存放和边相关的信息。

3. **构建无向图的过程**：
- 输入总顶点数和总边数。
- 输入点的信息并初始化每个表头节点的指针域为NULL。
- 创建邻接表。对每条边，确定这两个顶点的序号后，将此边节点分别插入两个对应的边链表的头部。

4. **算法分析**：该算法的时间复杂度是O(n+e)，其中n为顶点数，e为边数。

### 邻接表的优缺点：

**优点**：
1. 便于增加和删除顶点。
2. 便于统计边的数目。按顶点表顺序查找所有边表可以得到边的数目，时间复杂度为O(n+e)。
3. 空间效率高。适合表示稀

疏图。特别是对于一个具有n个顶点、e条边的图G, 如果G是无向图，邻接表表示中有n个顶点表节点和2e个边表节点；如果G是有向图，邻接表或逆邻接表表示中均有n个顶点表节点和e个边表节点。这意味着其空间复杂度为O(n+e)。而对于稠密图，由于邻接表中需要额外的链域，所以通常使用邻接矩阵表示法。

**缺点**：
1. 判断顶点之间是否有边不太方便。要判断两顶点v和v'之间是否存在边，可能需要查找整个边表。在最坏的情况下，时间复杂度可能达到O(n)。
2. 在有向图中计算顶点的度（进度和出度）不便捷。对于无向图，在邻接表中顶点v的度是其边表中的节点数量。但在有向图的邻接表中，边表中的节点数表示顶点v的出度，而计算其入度则较为困难，需要遍历所有顶点的边表。如果有向图使用逆邻接表表示，那么与邻接表表示正好相反：计算顶点的入度会很简单，但计算其出度会比较困难。

### 补充：
- 值得注意的是，图的邻接矩阵表示是唯一的，但其邻接表表示不是唯一。这是因为在邻接表表示中，各边表节点的链接次序取决于建立邻接表的算法和边的输入顺序。
- 邻接矩阵和邻接表是图的两种常用的存储结构，各自有其优点和缺点。选择哪种表示方法取决于具体的应用场景和所需的操作。

接下来的内容介绍十字链表，这是有向图的另一种存储结构，特别设计来方便地获取顶点的入度和出度。

**十字链表**:
十字链表是有向图的一种链表存储结构。在这种表示中，每个顶点关联两个链表：一个用于入度，另一个用于出度。

每个顶点都有一个表头。表头的两个字段指向两个链表：一个指向第一个入度边，另一个指向第一个出度边。每个边节点有几个字段，包括指向其起点和终点的指针、指向起点和终点的下一个边的指针以及存储与边相关的其他信息的字段。

**优点**:
1. 易于获取顶点的入度和出度。
2. 与邻接表相比，空间复杂度仍为O(n+e)，但提供了更多的方便性。

**缺点**:
1. 相对于邻接表，十字链表的结构更加复杂。
2. 对于无向图，使用十字链表可能过于冗余。

总的来说，选择最适合的图存储结构取决于所处理的具体问题和操作的频率。邻接矩阵在某些情境下可能更适合，而在其他情境下，邻接表或十字链表可能是更好的选择。

6.4.3 十字链表

### 6.4.3 十字链表

- **定义**：十字链表(Orthogonal List)是有向图的另一种链式存储结构。它将有向图的邻接表和逆邻接表结合起来，得到的一种链表。

- **组成**：
* **弧节点(ArcBox)**：
- tailvex：指示弧尾的顶点位置。
- headvex：指示弧头的顶点位置。
- hlink：指向弧头相同的下一条弧。
- tlink：指向弧尾相同的下一条弧。
- info：指向该弧的相关信息。

* **顶点节点(VexNode)**：
- data：存储与顶点相关的信息，例如顶点的名称。
- firstin：指向以该顶点为弧头的第一个弧节点。
- firstout：指向以该顶点为弧尾的第一个弧节点。

- **图示**：图6.14展示了一个有向图与其对应的十字链表。
- (a)有向图。
- (b)十字链表。

- **性质**：
1. 若将有向图的邻接矩阵看作稀疏矩阵，那么十字链表可以看作邻接矩阵的链式存储结构。
2. 弧节点所在的链表是非循环的，节点之间的相对位置自然形成，不必按照顶点序号排列。
3. 顶点节点之间的关系是顺序存储，而不是链接关系。- **存储表示**：

#define MAX_VERTEX_NUM 20typedef struct ArcBox {int tailvex, headvex;        // 弧的尾和头顶点的位置struct ArcBox *hlink, *tlink; // 分别为弧头相同和弧尾相同的弧的链域InfoType *info;             // 该弧的相关信息
} ArcBox;typedef struct VexNode {VertexType data;            // 与顶点相关的信息ArcBox *firstin, *firstout; // 分别指向该顶点的第一条入弧和出弧
} VexNode;typedef struct {VexNode xlist[MAX_VERTEX_NUM];int vexnum, arcnum;        // 有向图的当前顶点数和弧数
} OLGraph;

- **时间复杂度**：建立十字链表的时间复杂度与建立邻接表相同。使用十字链表可以容易地找到以v为尾的弧和以v为头的弧，从而容易求得顶点的出度和入度。

- **应用**：十字链表在某些有向图的应用中是一个非常有用的工具。

> **备注**：给定的信息片段是断断续续的，可能部分信息缺失或不完整。上面的笔记是根据提供的内容尽量整理得出的。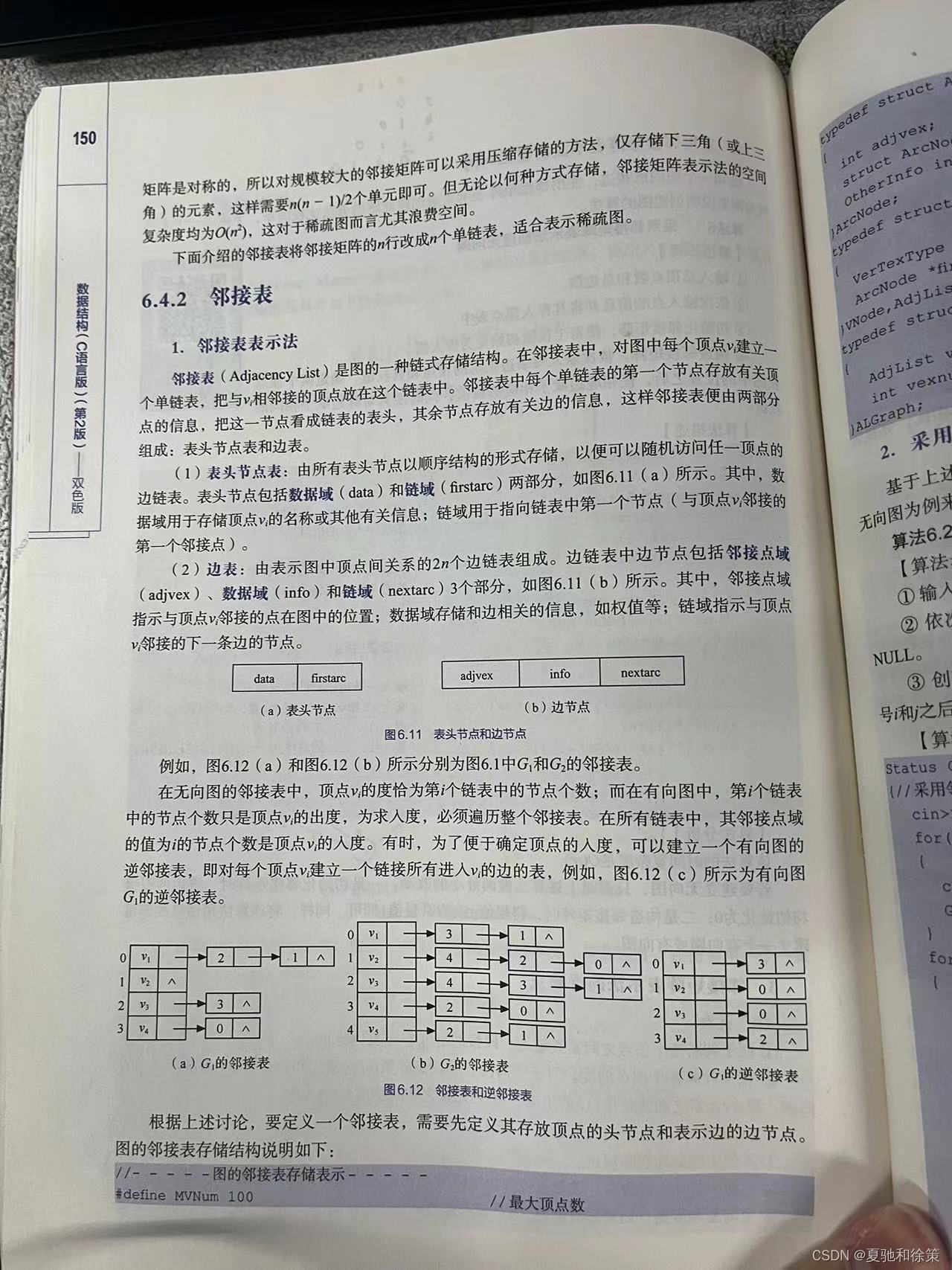

6.4.4 邻接多重表

**定义**:
邻接多重表(Adjacency Multilist)是无向图的链式存储结构，与邻接表类似，但在邻接多重表中，每条边用一个节点来表示，而不是两个。

**优势**:
相比邻接表，邻接多重表在某些对边操作的应用中更为方便。例如，对已经搜索过的边进行标记或删除某条边等，都更容易在邻接多重表中进行。

**结构描述**:

1. **边节点** (图6.15a):
- **mark**: 标志域，用以标记该条边是否被搜索过。
- **ivex, jvex**: 该边依附的两个顶点在图中的位置。
- **ilink**: 指向下一条依附于顶点ivex的边。
- **jlink**: 指向下一条依附于顶点jvex的边。
- **info**: 指针域，指向和边相关的信息。

2. **顶点节点** (图6.15b):
- **data**: 存储与顶点相关的信息。
- **firstedge**: 指示第一条依附于该顶点的边。

**示例**:
图6.16展示了无向图G₂的邻接多重表结构。可以看出，与邻接表相比，邻接多重表中每条边只用一个节点表示，减少了存储冗余。**邻接多重表的数据结构表示**:

#define MAX_VERTEX_NUM 20
typedef enum {unvisited, visited} VisitIf;typedef struct EBox {VisitIf mark;int ivex, jvex;struct EBox *ilink, *jlink;InfoType *info;
} EBox;typedef struct VexBox {VertexType data;EBox *firstedge;
} VexBox;typedef struct {VexBox adjmulist[MAX_VERTEX_NUM];int vexnum, edgenum;
} AMLGraph;

总结：
邻接多重表主要应用于需要频繁对边进行操作的场合。其优点是每条边只用一个节点表示，减少了存储冗余和某些操作的复杂度。但其也继承了链表的一些特性，如需要额外的指针域存储。选择适当的数据结构，取决于具体应用和操作的需求。