目录

拟合

欠拟合

过拟合

正确的拟合

解决过拟合的方法：正则化

---

线性回归模型和逻辑回归模型都存在欠拟合和过拟合的情况。

拟合

来自百度的解释：

数据拟合又称曲线拟合，俗称拉曲线，是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据，根据这些数据，我们往往希望得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合，这过程就叫做拟合(fitting)。

个人理解，拟合就是根据已有数据来建立的一个数学模型，这个数据模型能最大限度的包含现有的数据。这样预测的数据就能最大程度的符合现有情况。

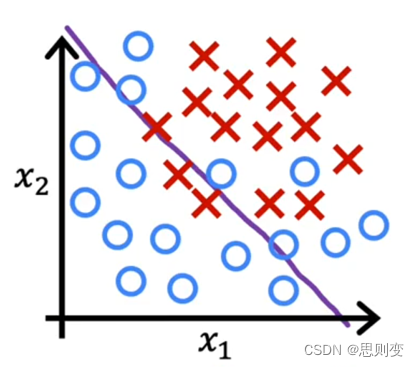
欠拟合

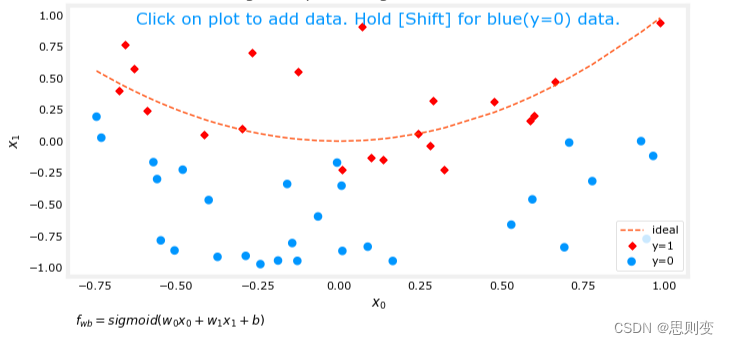
所建立的模型与现有数据匹配度较低如下图的分类模型，决策边界并不能很好的区分目前的数据

当训练数据的特征值较少的时候会出现欠拟合

过拟合

模型过于匹配现有数据，导致模型不能推广应用到更多数据中去。当训练数据的特征值太多的时候会出现这种情况。

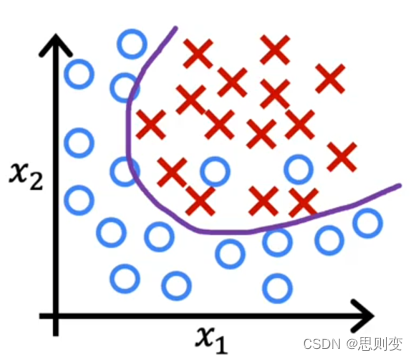
正确的拟合

介于欠拟合和过拟合之间

 

解决过拟合的方法：正则化

 解决过拟合的方法是将模型正则化，就是说把不是主要特征的w_j调整为无限接近于0，然后训练模型，这样来寻找最优的模型。这样存在一个问题，怎么分辨特征是不是主要特征呢？这个是不好分辨的，因此是把所有的特征都正则化，正则化的公式为:

线性回归cost function:

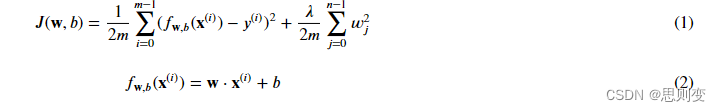
逻辑回归cost function:

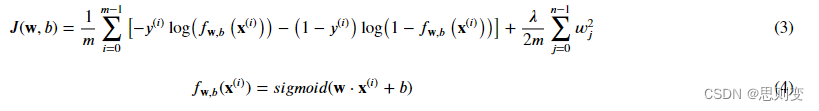
适用于线性回归和逻辑回归的梯度下降函数：

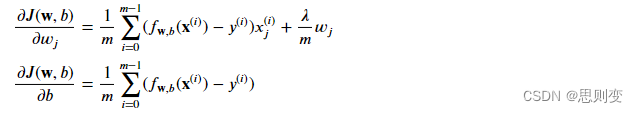
实现代码：

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from plt_overfit import overfit_example, outputnp.set_printoptions(precision=8)def sigmoid(z):"""Compute the sigmoid of zArgs:z (ndarray): A scalar, numpy array of any size.Returns:g (ndarray): sigmoid(z), with the same shape as z"""g = 1/(1+np.exp(-z))return gdef compute_cost_linear_reg(X, y, w, b, lambda_ = 1):"""Computes the cost over all examplesArgs:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters  b (scalar)      : model parameterlambda_ (scalar): Controls amount of regularizationReturns:total_cost (scalar):  cost """m  = X.shape[0]n  = len(w)cost = 0.for i in range(m):f_wb_i = np.dot(X[i], w) + b                                   #(n,)(n,)=scalar, see np.dotcost = cost + (f_wb_i - y[i])**2                               #scalar             cost = cost / (2 * m)                                              #scalar  reg_cost = 0for j in range(n):reg_cost += (w[j]**2)                                          #scalarreg_cost = (lambda_/(2*m)) * reg_cost                              #scalartotal_cost = cost + reg_cost                                       #scalarreturn total_cost                                                  #scalarnp.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print("Regularized cost:", cost_tmp)def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):"""Computes the cost over all examplesArgs:Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters  b (scalar)      : model parameterlambda_ (scalar): Controls amount of regularizationReturns:total_cost (scalar):  cost """m,n  = X.shapecost = 0.for i in range(m):z_i = np.dot(X[i], w) + b                                      #(n,)(n,)=scalar, see np.dotf_wb_i = sigmoid(z_i)                                          #scalarcost +=  -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)      #scalarcost = cost/m                                                      #scalarreg_cost = 0for j in range(n):reg_cost += (w[j]**2)                                          #scalarreg_cost = (lambda_/(2*m)) * reg_cost                              #scalartotal_cost = cost + reg_cost                                       #scalarreturn total_cost                                                  #scalarnp.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print("Regularized cost:", cost_tmp)def compute_gradient_linear_reg(X, y, w, b, lambda_): """Computes the gradient for linear regression Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters  b (scalar)      : model parameterlambda_ (scalar): Controls amount of regularizationReturns:dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. dj_db (scalar):       The gradient of the cost w.r.t. the parameter b. """m,n = X.shape           #(number of examples, number of features)dj_dw = np.zeros((n,))dj_db = 0.for i in range(m):                             err = (np.dot(X[i], w) + b) - y[i]                 for j in range(n):                         dj_dw[j] = dj_dw[j] + err * X[i, j]               dj_db = dj_db + err                        dj_dw = dj_dw / m                                dj_db = dj_db / m   for j in range(n):dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]return dj_db, dj_dwnp.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp =  compute_gradient_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )def compute_gradient_logistic_reg(X, y, w, b, lambda_): """Computes the gradient for linear regression Args:X (ndarray (m,n): Data, m examples with n featuresy (ndarray (m,)): target valuesw (ndarray (n,)): model parameters  b (scalar)      : model parameterlambda_ (scalar): Controls amount of regularizationReturnsdj_dw (ndarray Shape (n,)): The gradient of the cost w.r.t. the parameters w. dj_db (scalar)            : The gradient of the cost w.r.t. the parameter b. """m,n = X.shapedj_dw = np.zeros((n,))                            #(n,)dj_db = 0.0                                       #scalarfor i in range(m):f_wb_i = sigmoid(np.dot(X[i],w) + b)          #(n,)(n,)=scalarerr_i  = f_wb_i  - y[i]                       #scalarfor j in range(n):dj_dw[j] = dj_dw[j] + err_i * X[i,j]      #scalardj_db = dj_db + err_idj_dw = dj_dw/m                                   #(n,)dj_db = dj_db/m                                   #scalarfor j in range(n):dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]return dj_db, dj_dw  np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp =  compute_gradient_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )plt.close("all")
display(output)
ofit = overfit_example(True)

 逻辑回归输出为：