1 前言
retinex 是常见的图像增强的方法,retinex 是由两个单词合成的:retina + conrtex ,即视网膜+皮层。
2 建立的基础
Land 的 retinex theory 建立在三个假设之下:
- 真实世界是无色的,我们所谓的颜色是光和物质相互作用的结果。
- 每一颜色区域由给定波长的红、绿、蓝三原色构成。
- 每个单位区域的颜色由三原色决定。
3 算法理论的发展
- 单尺度 Retinex 算法 SSR (single scale retinex)
- 多尺度加权平均 Retinex 算法 MSR (multi-scale retinex)
- 带彩色恢复的多尺度 Retinex 算法 MSRCR(multi-scale retinex with color restoration)
4 算法理论
- 物体的颜色由物体对长波、中波、短波广西的反射能力决定,与反射光强度的绝对值无关。
- 物体的色彩不受光照非均性影响,具有一致性。即,retinex 以色感一致性(颜色恒常性)为基础。
- 不同于传统的线性、非线性的只能增强图像某一类特征的方法,Retinex可以在动态范围压缩、边缘增强和颜色恒常三个方面达到平衡,因此可以对各种不同类型的图像进行自适应的增强。
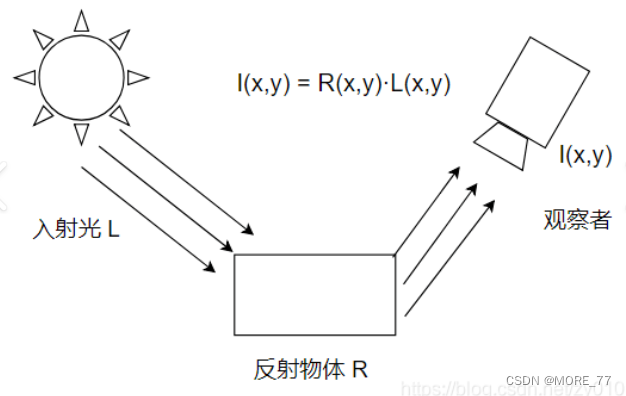
Retinex theory 认为图像 I ( x , y ) I(x,y) I(x,y)由两幅不同的图像构成:入射图像(亮度图像) L ( x , y ) L(x,y) L(x,y) + 反射图像 R ( x , y ) R(x,y) R(x,y)。
入射光照射到反射物体上,通过物体的反射,形成反射光进入人眼,最后形成图像。
用公式表示就是: I ( x , y ) = L ( x , y ) ∗ R ( x , y ) I(x,y)=L(x,y)*R(x,y) I(x,y)=L(x,y)∗R(x,y)
其中, L ( x , y ) L(x, y) L(x,y)表示入射光图像,环境光的照射分量,它直接决定了图像中像素所能达到的动态范围,应当尽量去除。 R ( x , y ) R(x,y) R(x,y)表示了物体的反射性质,即图像的内在属性,应尽量的保留。 I ( x , y ) I(x,y) I(x,y)表示人眼所能接收到的反射光图像。
L ( x , y ) L(x,y) L(x,y)的输入是光源的位置、强度、颜色,输出是物体表面上不同位置的照亮值。
R ( x , y ) R(x,y) R(x,y)的输入是物体表面的材质、颜色、法线,输出是表面不同位置的反射率和颜色。
Retinex 理论的基本思想:在原始图像中,通过某种方法去除或者降低入射图像 L ( x , y ) L(x,y) L(x,y)的影响,从而尽量的保留物体本质的反射属性图像 R ( x , y ) R(x,y) R(x,y)。
基于Retinex的图像增强的目的:从原始图像S中估计出光照L,从而分解出R,消除光照不均的影响,以改善图像的视觉效果,正如人类视觉系统那样。
根据亮度图像 L ( x , y ) L(x,y) L(x,y)估计方法的不同,先后涌现出了很多Retinex算法。
5 处理步骤
原理:
- 利用取对数的方法将照射光的分量与反射光分量分离:
l o g ( I ( x , y ) ) = l o g ( L ( x , y ) ) + l o g ( R ( x , y ) ) log(I(x,y))=log(L(x,y))+log(R(x,y)) log(I(x,y))=log(L(x,y))+log(R(x,y))
(因为对数形式与人类在感受亮度的过程属性最相近) - 用高斯模板对图像做卷积,近似获得入射图像 L ( x , y ) L(x,y) L(x,y)
- 使用步骤1的公式,获得反射图像 R ( x , y ) = e x p ( l o g ( I ( x , y ) ) − l o g ( L ( x , y ) ) ) R(x,y)=exp(log(I(x,y))-log(L(x,y))) R(x,y)=exp(log(I(x,y))−log(L(x,y)))
- 对 R ( x , y ) R(x,y) R(x,y)做对比度增强,得到最终的结果图像。
实际操作:
- 用高斯模板对原图像做卷积,相当于对原图做低通滤波,得到低通滤波后的图像D(x,y),其中F(x,y)表示高斯滤波函数。
D ( x , y ) = I ( x , y ) ∗ F ( x , y , σ ) D(x,y)=I(x,y)*F(x,y,σ) D(x,y)=I(x,y)∗F(x,y,σ) - 在对数域中,用原图像减去低通滤波图像,得到高频增强的图像G(x,y)
G ( x , y ) = l o g ( I ( x , y ) ) − l o g ( D ( x , y ) ) G(x,y)=log(I(x,y))-log(D(x,y)) G(x,y)=log(I(x,y))−log(D(x,y)) - 对G(x,y)取反对数,得到增强后的图像:
R ( x , y ) = e x p ( G ( x , y ) ) R(x,y)=exp(G(x,y)) R(x,y)=exp(G(x,y)) - 对 R ( x , y ) R(x,y) R(x,y)做对比度增强,得到最终的结果图像。
6 SSR 算法
具体步骤如下:
- 输入原始图像 I ( x , y ) I(x,y) I(x,y) 和滤波的半径范围 s i g m a σ sigma \ σ sigma σ ;
- 计算原始图像 I ( x , y ) I(x,y) I(x,y)高斯滤波后的结果,得到 L ( x , y ) L(x,y) L(x,y);
- 按照公式计算,得到 l o g [ R ( x , y ) ] log[R(x,y)] log[R(x,y)];
- 将得到的结果量化为 [0, 255] 范围的像素值,然后输出结果图像。
需要注意的是,最后一步量化的过程中,并不是将 l o g [ R ( x , y ) ] log[R(x,y)] log[R(x,y)] 进行 e x p exp exp 量化得到 R ( x , y ) R(x,y) R(x,y) ,而是直接将 l o g [ R ( x , y ) ] log[R(x,y)] log[R(x,y)] 的结果直接用如下公式进行量化:
R ( x , y ) = V a l u e − M i n M a x − M i n ∗ 255 R(x,y)=\frac{Value-Min}{Max-Min}*255 R(x,y)=Max−MinValue−Min∗255
上述过程整合起来:
R S S R ( x , y , σ ) = l o g ( I ( x , y ) ) − l o g ( I ( x , y ) ∗ F ( x , y , σ ) ) R_{SSR}(x,y,σ)=log(I(x,y))-log(I(x,y)*F(x,y,σ)) RSSR(x,y,σ)=log(I(x,y))−log(I(x,y)∗F(x,y,σ))
R 表示在对数域的输出。
7 MSR 算法
多尺度视网膜算法是在 SSR 算法的基础上提出的,采用多个不同的 s i g m a σ sigma σ sigmaσ值,然后将最后得到的不同结果进行加权取值,公式如下所示:
R M S R ( x , y , σ ) = ∑ k = 1 n w k R S S R k ( x , y , σ k ) R_{MSR}(x,y,σ)=\sum_{k=1}^nw_kR_{SSR_k}(x,y,σ_k) RMSR(x,y,σ)=∑k=1nwkRSSRk(x,y,σk)
其中 n n n 是尺度的数量, σ = σ 1 , σ 2 , . . . , σ n σ= {σ_1,σ_2,...,σ_n} σ=σ1,σ2,...,σn 是高斯模糊系数的向量, w k w_k wk是与第 k 个尺度相关的权重,其中 w 1 + w 2 + . . . + w n = 1 w_1 + w_2 + ... + w_n = 1 w1+w2+...+wn=1 。(权重一般都为1/N)
优点是可以同时保持图像高保真度与对图像的动态范围进行压缩的同时,MSR也可实现色彩增强、颜色恒常性、局部动态范围压缩、全局动态范围压缩,也可以用于X光图像增强。
一般的Retinex算法对光照图像估计时,都会假设初始光照图像是缓慢变化的,即光照图像是平滑的。但实际并非如此,亮度相差很大区域的边缘处,图像光照变化并不平滑。所以在这种情况下,Retinuex增强算法在亮度差异大区域的增强图像会产生光晕。
另外MSR常见的缺点还有边缘锐化不足,阴影边界突兀,部分颜色发生扭曲,纹理不清晰,高光区域细节没有得到明显改善,对高光区域敏感度小等。
8 MSRCR 算法
在前面的增强过程中,图像可能会因为增加了噪声,而使得图像的局部细节色彩失真,不能显现出物体的真正颜色,整体视觉效果变差。针对这一点不足,MSRCR在MSR的基础上,加入了色彩恢复因子C来调节由于图像局部区域对比度增强而导致颜色失真的缺陷:
R M S R C R ( x , y , σ ) = β l o g ( α I i ( x , y ) ∑ j = 1 3 I j ( x , y ) ) R M S P i ( x , y , σ ) R_{MSRCR}(x,y,σ)=βlog(\frac{αI_i(x,y)}{\sum_{j=1}^3I_j(x,y)})R_{MSP_i}(x,y,σ) RMSRCR(x,y,σ)=βlog(∑j=13Ij(x,y)αIi(x,y))RMSPi(x,y,σ)
- I i ( x , y ) I_i(x, y) Ii(x,y) 表示第 i 个通道的图像
- C i C_i Ci 表示第 i 个通道的彩色恢复因子,用来调节3个通道颜色的比例;
- β 是增益常数;
- α 是受控制的非线性强度;
MSRCR算法利用彩色恢复因子C,调节原始图像中3个颜色通道之间的比例关系,从而把相对较暗区域的信息凸显出来,达到了消除图像色彩失真的缺陷。
处理后的图像局部对比度提高,亮度与真实场景相似,在人们视觉感知下,图像显得更加逼真。

参考博文
1. csdn参考博文
2. 知乎参考博文
3. csdn参考博文





MySQL5.7编码设置)













