🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

算法空间复杂度的定义
算法的时间复杂度和空间复杂度是度量算法好坏的两个重要量度,在实际写代码的过程中,我们完全可以用空间来换时间,比如说,我们要判断某某年是不是闰年,大家可能第一时间想到的都是写一个算法来判断每次输入的年份符不符合闰年的条件.但其实还有种方法是,我们可以事先建立一个有2050个元素的数组(年数比现实略多一点),然后把所有年份按下标数字对应,如果是闰年,此数组项的值设为1,否则设为0.这样,判断某年是否是闰年,就只需要查找一下对应数组项的值就可以了.这样求闰年的时间复杂度为O(1).既然空间复杂度这么好用,接下来我们就来一起学习它的基本内容吧.
上篇文章中我们一起探讨了算法的时间复杂度的相关知识,在这节我们将一起探讨算法的空间复杂度的相关知识.
先来看算法空间复杂度的定义:
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)=O(f(n)).
其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数.
通过上节对时间复杂度的分析可知,算法的时间复杂度不是用来计算程序具体耗时的,同样的,空间复杂度也不是用来计算程序实际占用的空间的.
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用S(n)来定义.
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐近表示法.
注意:函数运行时所需要的栈空间(存储参数,局部变量,一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时侯显示申请的额外空间来确定.
一般情况下,算法要占据的空间可以分为两部分:
- 算法本身要占据的空间,输入和输出,指令,常数,变量等.
- 算法要使用的辅助空间.
第一条大家应该很好理解,一个程序在机器上执行时,需要存储程序本身的指令,常数,变量和输入数据.
除此之外,还需要存储对数据操作的存储单元,对数据操作的存储单元即算法的辅助空间.
我们参照一个实际程序(冒泡排序函数)来理解一下这个概念:
//冒泡排序函数
void bubbleSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){// 交换arr[j]和arr[j+1]int temp = arr[j]; //变量temp占据的空间就是辅助空间arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}如上,在冒泡排序函数中,我们需要开辟一个整形变量temp,它占据4个字节,这4个字节的空间就是冒泡排序算法在运行过程中要使用的辅助空间.
至于其他的变量i,j或是数组arr,则都属于算法本身要占据的空间,即无论使不使用冒泡排序算法程序运行都要使用的空间.这部分空间不计入算法空间复杂度的度量.
常见的空间复杂度
📌常数阶
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为O(1).
再拿上面的冒泡排序举例:
//冒泡排序函数
void bubbleSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){// 交换arr[j]和arr[j+1]int temp = arr[j]; //变量temp每次进入if语句创建,出if语句销毁arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}可以看到,算法在运行过程中,虽然会循环很多次交换arr[j]和arr[j+1]的操作,但在这过程中创建的变量temp每次都是进入if语句后被创建,出if语句后被销毁,因此即便创建temp的语句运行的次数随n的增大在不断变多,但其本质上用的都是同一块空间,不论n大小如何变化,temp占用的空间大小都不会变化,因此冒泡排序的空间复杂度为O(1).
📌线性阶
如果算法执行所需要的临时空间随着某个变量n的大小呈线性变化,即此算法空间复杂度为一个线性阶,可表示为O(n).
假设我们现在要求出从0开始的n个素数,将它们存储在数组arr中,代码如下:
int main()
{int i, j,k, flag;int n; int arr[n] = { 0 }; //仅作示例演示,正式编程时变量不能作为数组长度for (i = 0; k < n; i++){flag = 1;for (j = 2; j < i; j++){if (i % j == 0){flag = 0;break;}}if (flag == 1){arr[k] = i;k++;}}return 0;
}在这个程序中我们就需要开辟长度为n的数组来存放我们求得的n个素数.显而易见,开辟的数组长度n是随着问题规模的n增长而增长的,且呈线性相关,因此该程序的空间复杂度为O(n).
常见的时间复杂度及其耗费空间排序
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| 5201314 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
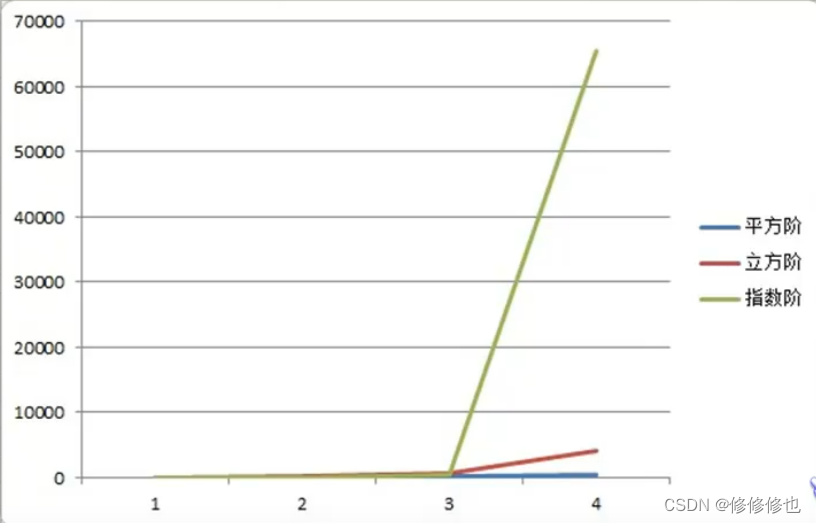
| 3n^2+2n+1 | O(n^2) | 平方阶 |
| O(logn) | 对数阶 | |
| O(nlogn) | nlogn阶 | |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
常用的空间复杂度所耗费的空间从小到大依次是:

结语
当我们搞清楚算法的空间复杂度后,数据结构算法篇的内容就结束了,接下来我们将开启数据结构新的章节——线性表,在新章节中我们将一起学习如何实现顺序表,单链表,双链表,循环链表等相关知识.希望这些内容能对大家有所帮助,一起学习,一起进步!
相关文章推荐
【数据结构】什么是数据结构?
【数据结构】什么是算法?
【数据结构】算法效率的度量方法
【数据结构】算法的时间复杂度
【C语言】冒泡排序
【数据结构】什么是线性表?
......

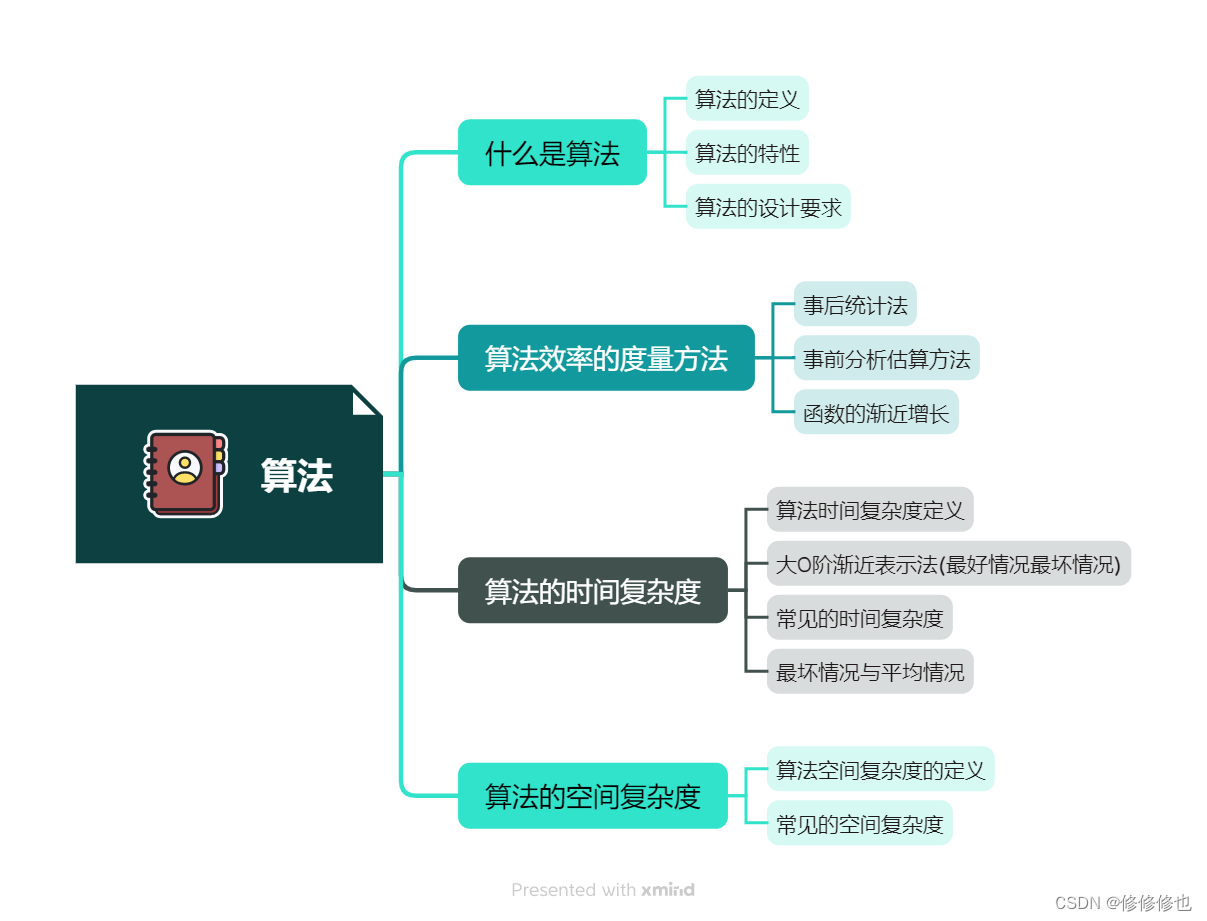
数据结构算法篇思维导图:

)
)


)













)