软间隔与正则化
- 问题一:优化目标函数是如何得到的?得到的过程是怎样的?
- 问题二:拉格朗日乘子法计算详细过程
- 问题三:KKT条件求解过程
- 问题四:结构风险最小化(SRM)的原理
在前面的讨论中,我们一直假定训练样本在样本空间或特征空间中是
线性可分的,即存在一个超平面能将不同类的样本完全划分开.然而,在现实任务中往往 很难确定合适的核函数 使得训练样本在特征空间中线性可分;
退一步说,即便恰好找到了某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的.
问题一:优化目标函数是如何得到的?得到的过程是怎样的?
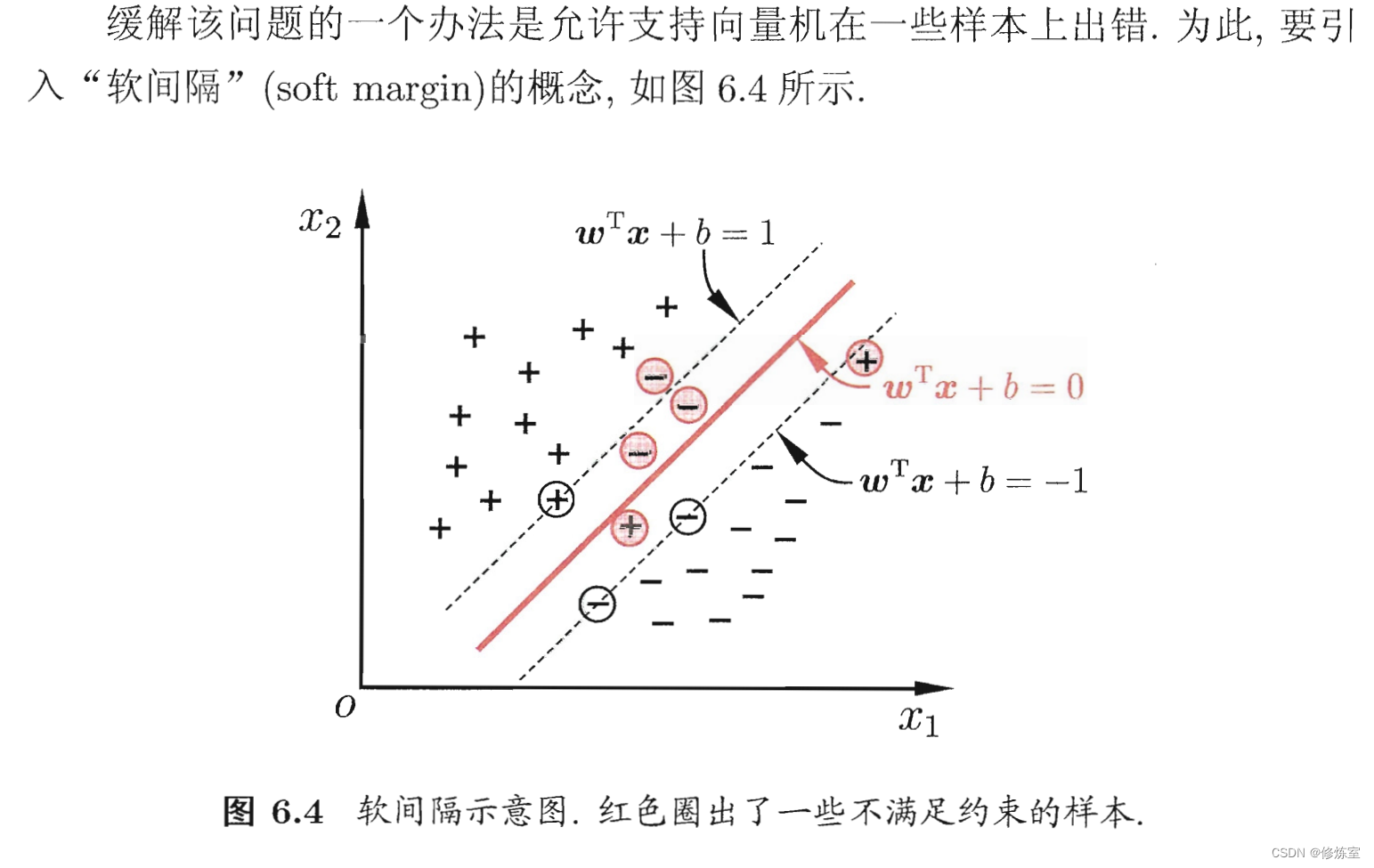
软间隔SVM是对传统的硬间隔SVM的扩展,它允许某些数据点违反最初的分类边界。这样做的目的是提高模型对噪声和异常值的鲁棒性,从而获得更好的泛化能力。在这个设置中,优化目标函数的推导过程是这样的:
-
软间隔引入:为了应对现实世界数据中的噪声和不完全线性可分的情况,引入软间隔的概念。在硬间隔SVM中,所有数据点都严格满足 y i ( w T x i + b ) ≥ 1 y_i (w^T x_i + b) \geq 1 yi(wTxi+b)≥1 的约束。在软间隔SVM中,我们允许某些点不满足这个条件,引入松弛变量 ξ i \xi_i ξi 来衡量每个数据点违背间隔的程度。
-
优化目标函数:考虑到间隔违规和模型的复杂度,我们希望最小化一个包含正则化项(控制模型复杂度)和损失项(衡量间隔违规)的目标函数。因此,目标函数变为最小化 1 2 ∥ w ∥ 2 \frac{1}{2} \|w\|^2 21∥w∥2(正则化项)加上 C ∑ ξ i C \sum \xi_i C∑ξi(损失项),其中 C C C 是一个正的正则化参数,用于平衡两者之间的重要性。
-
调整约束:每个数据点的原始约束 y i ( w T x i + b ) ≥ 1 y_i (w^T x_i + b) \geq 1 yi(wTxi+b)≥1 被调整为 y i ( w T x i + b ) ≥ 1 − ξ i y_i (w^T x_i + b) \geq 1 - \xi_i yi(wTxi+b)≥1−ξi,同时确保松弛变量 ξ i \xi_i ξi 是非负的。
-
替代损失函数:松弛变量 ξ i \xi_i ξi 对应于 ℓ 0 / 1 \ell_0/1 ℓ0/1 损失函数的替代。在优化过程中,由于 ℓ 0 / 1 \ell_0/1 ℓ0/1 损失函数不是 连续的 ,
不易优化,通常会采用其他连续可微的损失函数,如 hinge 损失函数 或 对数 损失函数。
- hinge 损失: l hinge ( z ) = max ( 0 , 1 − z ) l_{\text{hinge}}(z) = \max(0, 1 - z) lhinge(z)=max(0,1−z);
- 指数损失(exponential loss): l exp ( z ) = exp ( − z ) l_{\text{exp}}(z) = \exp(-z) lexp(z)=exp(−z);
- 对数损失(logistic loss): l log ( z ) = log ( 1 + exp ( − z ) ) l_{\text{log}}(z) = \log(1 + \exp(-z)) llog(z)=log(1+exp(−z)).

5. 最终优化问题:考虑到以上的点,我们的最终优化问题形式化为:
minimize w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i \text{minimize}_{w,b,\xi} \quad \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{m} \xi_i minimizew,b,ξ21∥w∥2+Ci=1∑mξi
subject to y i ( w T x i + b ) ≥ 1 − ξ i , ξ i ≥ 0 , i = 1 , … , m . \text{subject to} \quad y_i(w^T x_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad i=1, \ldots, m. subject toyi(wTxi+b)≥1−ξi,ξi≥0,i=1,…,m.
在这个过程中,软间隔的引入以及对目标函数的修改都是为了使模型更适应实际数据集的复杂性。正则化参数 C C C 的选择变得至关重要,因为它直接影响模型对数据中噪声的容忍程度和防止过拟合的能力。通过合理设置 C C C,模型可以在保持足够间隔的同时,允许某些数据点的违规,从而在保持模型泛化能力的前提下,最小化总体损失。
问题二:拉格朗日乘子法计算详细过程
-
定义问题和约束:
- 原始的SVM问题是最大化间隔,等价于最小化 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^2 21∥w∥2 。
- 我们要求每个数据点至少有一个距离超平面的函数间隔1。在软间隔SVM中,我们允许函数间隔小于1,但这种违规要受到惩罚。
- 引入松弛变量 ξ i \xi_i ξi 来度量第 ( i ) 个数据点的间隔违规程度。
-
引入拉格朗日乘子:
- 对每个数据点 ( i ),我们有两个约束:函数间隔 y i ( w T x i + b ) ≥ 1 − ξ i y_i(w^T x_i + b) \geq 1 - \xi_i yi(wTxi+b)≥1−ξi 和松弛变量 ξ i ≥ 0 \xi_i \geq 0 ξi≥0
- 为这两个约束引入两组拉格朗日乘子 α i \alpha_i αi 和 μ i \mu_i μi,它们必须满足 α i ≥ 0 \alpha_i \geq 0 αi≥0 和 μ i ≥ 0 \mu_i \geq 0 μi≥0
-
构建拉格朗日函数:
- 对于每个数据点 ( i ),对应的拉格朗日函数部分是 α i ( 1 − ξ i − y i ( w T x i + b ) ) \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) αi(1−ξi−yi(wTxi+b)) 和 μ i ξ i \mu_i \xi_i μiξi。
- 所有数据点的拉格朗日函数相加,我们得到总拉格朗日函数
- L ( w , b , α , ξ , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i L(w, b, \alpha, \xi, \mu) = \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{m} \xi_i + \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) - \sum_{i=1}^{m} \mu_i \xi_i L(w,b,α,ξ,μ)=21∥w∥2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wTxi+b))−i=1∑mμiξi
- 这里 C C C 是一个预先设定的正则化参数,它平衡了间隔的宽度和违规程度。
-
拉格朗日对偶问题:
- 通过对 L L L 关于 w w w 、 b b b 和 ξ \xi ξ 求偏导并设为0,我们可以得到 w w w 、 b b b 和 ξ \xi ξ 的表达式,然后将它们从拉格朗日函数中消除,得到只关于 α \alpha α 和 μ \mu μ 的函数。
- 对 ( w ) 求偏导:
针对拉格朗日函数中与 w w w 相关的部分 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^2 21∥w∥2 和 ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) ∑i=1mαi(1−ξi−yi(wTxi+b)),我们分别对其求偏导。
首先,对 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^2 21∥w∥2 求偏导: ∂ L ∂ w = w \frac{\partial L}{\partial w} = w ∂w∂L=w
然后,对 ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) ∑i=1mαi(1−ξi−yi(wTxi+b)) 求偏导: ∂ L ∂ w = − ∑ i = 1 m α i y i x i \frac{\partial L}{\partial w} = -\sum_{i=1}^{m} \alpha_i y_i x_i ∂w∂L=−i=1∑mαiyixi
最终,令两者相等并设为零,我们有: w − ∑ i = 1 m α i y i x i = 0 w - \sum_{i=1}^{m} \alpha_i y_i x_i = 0 w−i=1∑mαiyixi=0- 对 ( b ) 求偏导:
针对拉格朗日函数中与 ( b ) 相关的部分 ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) ∑i=1mαi(1−ξi−yi(wTxi+b)),我们对其求偏导。
对 ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) ∑i=1mαi(1−ξi−yi(wTxi+b)) 求偏导:
∂ L ∂ b = − ∑ i = 1 m α i y i \frac{\partial L}{\partial b} = -\sum_{i=1}^{m} \alpha_i y_i ∂b∂L=−i=1∑mαiyi
令其等于零,得到:
− ∑ i = 1 m α i y i = 0 -\sum_{i=1}^{m} \alpha_i y_i = 0 −i=1∑mαiyi=0- 对 ξ \xi ξ 求偏导:
针对拉格朗日函数中与 ξ \xi ξ 相关的部分 C ∑ i = 1 m ξ i − ∑ i = 1 m μ i ξ i C\sum_{i=1}^{m} \xi_i - \sum_{i=1}^{m} \mu_i \xi_i C∑i=1mξi−∑i=1mμiξi,我们对其求偏导。
对 C ∑ i = 1 m ξ i − ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i C\sum_{i=1}^{m} \xi_i - \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) - \sum_{i=1}^{m} \mu_i \xi_i C∑i=1mξi−∑i=1mαi(1−ξi−yi(wTxi+b))−∑i=1mμiξi 求偏导: ∂ L ∂ ξ i = C − α i − μ i \frac{\partial L}{\partial \xi_i} = C - \alpha_i - \mu_i ∂ξi∂L=C−αi−μi
令其等于零,得到:
C − α i − μ i = 0 对所有的 i C - \alpha_i - \mu_i = 0 \quad \text{对所有的} i C−αi−μi=0对所有的i
得到结果
w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=i=1∑mαiyixi
∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 i=1∑mαiyi=0
C = α i + μ i C = \alpha_i + \mu_i C=αi+μi
- 得到对偶优化问题:
- 消除 w w w、 b b b 和 ξ \xi ξ 后,我们得到对偶问题的最大化问题,仅关于 α \alpha α:
max α [ ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m y i y j α i α j x i T x j ] \max_{\alpha} \left[ \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} y_i y_j \alpha_i \alpha_j x_i^T x_j \right] αmax[i=1∑mαi−21i,j=1∑myiyjαiαjxiTxj] - 并且要满足约束 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0 和 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C
- 消除 w w w、 b b b 和 ξ \xi ξ 后,我们得到对偶问题的最大化问题,仅关于 α \alpha α:
根据KKT(Karush-Kuhn-Tucker)条件,对于每个数据点 x i x_i xi,如果 α i = 0 \alpha_i = 0 αi=0,那么该数据点不会对模型的决策边界造成影响;如果 0 < α i < C 0 < \alpha_i < C 0<αi<C,那么 x i x_i xi 是支持向量,并且处在边界上;如果 α i = C \alpha_i = C αi=C,那么数据点 x i x_i xi 被误分类,或者它恰好在边界的违反侧上。
- 当 (\alpha_i = 0) 时:
- 这意味着对应的数据点 x i x_i xi 不对模型的优化造成任何影响,也就是说它不是支持向量。这些点要么被
正确分类且 远离决策边界 ,要么在软间隔SVM中,这些点虽然被误分类但由于它们的影响在优化过程中被允许忽略(即对总损失的贡献被限制在了可接受的成本 C C C 内)。- 当 (0 < \alpha_i < C) 时:
- 这表示数据点 x i x_i xi 恰好在
边界上,即它是一个 支持向量 。在SVM中,这些支持向量决定了最终的决策边界。它们恰好位于或者非常接近我们希望数据点分界的边界线。- 当 (\alpha_i = C) 时:
- 这表示数据点 x i x_i xi 在优化过程中发挥了最大的影响,可能是因为它被误分类,或者即便它被正确分类,也位于边界内侧 紧邻决策边界 的地方。在软间隔SVM中,这代表该点被允许违反
最大间隔距离,但是由于其 α i \alpha_i αi 值达到了上限 C C C,这种违反的程度受到了约束。
当我们将拉格朗日函数 L ( α , μ ) L(\alpha, \mu) L(α,μ) 展开后,我们需要消除 w w w 和 (b),以及处理约束条件:
-
消除 w w w 和 (b):
我们已经有了 w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=∑i=1mαiyixi 和约束条件 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0 。我们代入 w w w 的表达式和约束条件:
L ( α , μ ) = 1 2 ∥ ∑ i = 1 m α i y i x i ∥ 2 + C ∑ i = 1 m ( C − α i − μ i ) + ∑ i = 1 m α i ( 1 − ( C − α i − μ i ) − y i ( ( ∑ j = 1 m α j y j x j ) T x i ) ) − ∑ i = 1 m μ i ( C − α i − μ i ) \begin{align*} L(\alpha, \mu) &= \frac{1}{2}\left\| \sum_{i=1}^{m} \alpha_i y_i x_i \right\|^2 + C\sum_{i=1}^{m} (C - \alpha_i - \mu_i) \\ &\quad + \sum_{i=1}^{m} \alpha_i \left(1 - (C - \alpha_i - \mu_i) - y_i\left(\left(\sum_{j=1}^{m} \alpha_j y_j x_j\right)^T x_i\right)\right) \\ &\quad - \sum_{i=1}^{m} \mu_i (C - \alpha_i - \mu_i) \end{align*} L(α,μ)=21 i=1∑mαiyixi 2+Ci=1∑m(C−αi−μi)+i=1∑mαi 1−(C−αi−μi)−yi (j=1∑mαjyjxj)Txi −i=1∑mμi(C−αi−μi)
我们可以进一步化简上述表达式。
-
化简 ∥ ∑ i = 1 m α i y i x i ∥ 2 \| \sum_{i=1}^{m} \alpha_i y_i x_i \|^2 ∥∑i=1mαiyixi∥2【内积展开】:
注意到 ∥ ∑ i = 1 m α i y i x i ∥ 2 \| \sum_{i=1}^{m} \alpha_i y_i x_i \|^2 ∥∑i=1mαiyixi∥2 可以写为 ( ∑ i = 1 m α i y i x i ) T ( ∑ i = 1 m α i y i x i ) (\sum_{i=1}^{m} \alpha_i y_i x_i)^T (\sum_{i=1}^{m} \alpha_i y_i x_i) (∑i=1mαiyixi)T(∑i=1mαiyixi)。展开后得到:
∥ ∑ i = 1 m α i y i x i ∥ 2 = ( ∑ i = 1 m α i y i x i ) T ( ∑ i = 1 m α i y i x i ) = ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \| \sum_{i=1}^{m} \alpha_i y_i x_i \|^2 = (\sum_{i=1}^{m} \alpha_i y_i x_i)^T (\sum_{i=1}^{m} \alpha_i y_i x_i) = \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j ∥i=1∑mαiyixi∥2=(i=1∑mαiyixi)T(i=1∑mαiyixi)=i=1∑mj=1∑mαiαjyiyjxiTxj
-
代入约束条件 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0:
由于约束条件是 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0,我们可以将 μ \mu μ 表达为 μ i = C − α i \mu_i = C - \alpha_i μi=C−αi。
-
代入上述结果到拉格朗日函数:
代入上述结果后,我们得到:
L ( α ) = ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m α i α j y i y j x i T x j \begin{align*} L(\alpha) &= \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j \end{align*} L(α)=i=1∑mαi−21i,j=1∑mαiαjyiyjxiTxj
以上步骤消除了 w w w 和 (b),并将 L ( α , μ ) L(\alpha, \mu) L(α,μ) 表达为关于 α \alpha α 的函数。
-
最大化 L ( α ) L(\alpha) L(α):
我们的目标是最大化 L ( α ) L(\alpha) L(α),即求解:
max α [ ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m y i y j α i α j x i T x j ] \max_{\alpha} \left[ \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} y_i y_j \alpha_i \alpha_j x_i^T x_j \right] αmax[i=1∑mαi−21i,j=1∑myiyjαiαjxiTxj]
并且要满足约束条件:
{ ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , . . . , m \begin{cases} \sum_{i=1}^{m} \alpha_i y_i = 0 \\ 0 \leq \alpha_i \leq C, \quad i = 1, 2, ..., m \end{cases} {∑i=1mαiyi=00≤αi≤C,i=1,2,...,m
问题三:KKT条件求解过程
和前面相比,两者唯一差别就在约束条件不同;

了解KKT条件的推导过程首先要理解拉格朗日乘子法在处理优化问题时如何使用。在软间隔支持向量机中,我们希望最小化以下拉格朗日函数:
L ( w , b , α , ξ , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i L(w, b, \alpha, \xi, \mu) = \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{m} \xi_i + \sum_{i=1}^{m} \alpha_i (1 - \xi_i - y_i(w^T x_i + b)) - \sum_{i=1}^{m} \mu_i \xi_i L(w,b,α,ξ,μ)=21∥w∥2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wTxi+b))−i=1∑mμiξi
其中, α \alpha α 和 μ \mu μ 是拉格朗日乘子, ξ \xi ξ 是松弛变量。
这个函数结合了目标函数和对每个样本 x i x_i xi 的约束,其中 y i ( w T x i + b ) ≥ 1 − ξ i y_i(w^T x_i + b) \geq 1 - \xi_i yi(wTxi+b)≥1−ξi。由于 ξ i \xi_i ξi 允许一定的分类违规,我们加入正则化参数 C C C 以限制这种违规。
KKT条件是最优解必须满足的一组条件,它们来自拉格朗日函数 L L L 关于每个变量的偏导数等于零的必要条件。下面是KKT条件:
- α i ≥ 0 \alpha_i \geq 0 αi≥0 和 μ i ≥ 0 \mu_i \geq 0 μi≥0:这确保了拉格朗日乘子是
非负的。在优化问题中,拉格朗日乘子用来 加权约束条件 ,而这个权重不能是负的。 - y i f ( x i ) − 1 + ξ i ≥ 0 y_i f(x_i) - 1 + \xi_i \geq 0 yif(xi)−1+ξi≥0 :这是
原始问题的约束,表示每个数据点的函数间隔至少为1,满足 1 − ξ i 1 - \xi_i 1−ξi(如果数据点被正确分类且在正确的间隔边界上或者超出间隔边界)。如果 ξ i > 0 \xi_i > 0 ξi>0,则该数据点有分类违规。 - α i ( y i f ( x i ) − 1 + ξ i ) = 0 \alpha_i(y_i f(x_i) - 1 + \xi_i) = 0 αi(yif(xi)−1+ξi)=0 :
互补松弛性条件。如果 α i > 0 \alpha_i > 0 αi>0,则对应的 y i f ( x i ) − 1 + ξ i y_i f(x_i) - 1 + \xi_i yif(xi)−1+ξi 必须等于0。这意味着对于非零 α i \alpha_i αi 的数据点,它们要么恰好在决策边界上,要么就是被 错误分类 的点。 - ξ i ≥ 0 \xi_i \geq 0 ξi≥0:
松弛变量的非负性,允许某些数据点违背硬间隔条件。 - μ i ξ i = 0 \mu_i \xi_i = 0 μiξi=0:这是对 μ \mu μ 的
互补松弛性条件,表明如果松弛变量 ξ i > 0 \xi_i > 0 ξi>0,即有分类违规,那么对应的 μ i \mu_i μi 必须是 0,反之亦然。
通过拉格朗日函数的偏导数等于零的条件和这些KKT条件,我们能够定义出最优化问题的对偶形式,这在数值上往往更易于求解。对偶问题通常涉及 仅有 α \alpha α 的最大化问题 ,而不直接求解 w w w 和 b b b,这简化了问题的复杂度,特别是当用核技巧将其扩展到高维空间时。
在实际算法实现中,如SMO算法,这种对偶形式是解决SVM最优化问题的关键。
问题四:结构风险最小化(SRM)的原理
结构风险最小化(SRM)的原理,它是支持向量机(SVM)理论的一个核心概念。结构风险最小化致力于在保证模型复杂度的同时 最小化训练误差 ,以达到良好的泛化效果。文中提到了经验风险(即模型在训练集上的误差)和模型的复杂度两个部分。具体来说,它通过一个优化问题来平衡这两者:
- 经验风险:是模型在训练数据上的 损失函数值的总和 。
- 正则化项:是用于控制 模型复杂度 的项,通常是模型参数的某种形式(如权重向量的范数)。
优化目标是最小化这两个量的组合,通常表示为:
min f Ω ( f ) + C ∑ i = 1 m L ( f ( x i ) , y i ) \min_f \quad \Omega(f) + C \sum_{i=1}^{m} L(f(x_i), y_i) fminΩ(f)+Ci=1∑mL(f(xi),yi)
这里, Ω ( f ) \Omega(f) Ω(f) 是正则化项, L ( f ( x i ) , y i ) L(f(x_i), y_i) L(f(xi),yi) 是损失函数, C C C 是控制两者权重的正则化参数。
了解SRM的概念可以帮助你更好地理解SVM模型的目标和设计背后的 动机 ,但如果你只是想实现算法而不关心其理论基础,你可以选择不深入这部分内容。然而,如果你打算深入理解SVM的工作原理或者进行算法的改进,那么对SRM的理解是很重要的。













)
![[力扣]——125.验证回文串](http://pic.xiahunao.cn/[力扣]——125.验证回文串)




