1翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
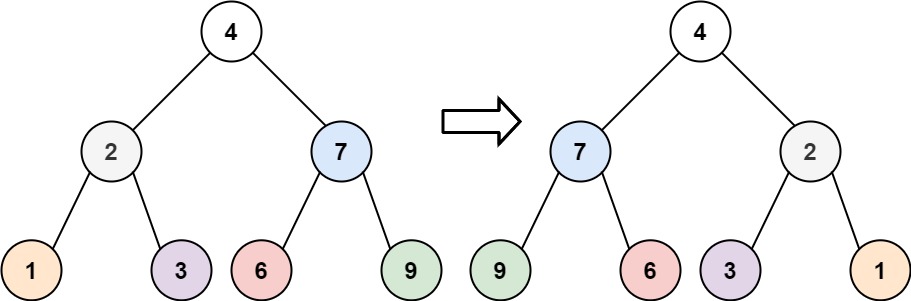
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:

输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
递归思路:
- 首先,检查根节点是否为空,如果为空则直接返回空节点。
- 对于每个非空节点,交换其左右子树(即将左子树和右子树进行交换)。
- 递归地对左子树调用
invertTree函数,实现左子树的翻转。 - 递归地对右子树调用
invertTree函数,实现右子树的翻转。 - 最后返回根节点,完成整棵二叉树的翻转操作。
递归代码:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right); // 交换左右子树invertTree(root->left); // 递归处理左子树invertTree(root->right); // 递归处理右子树return root;}
};迭代思路:
首先检查根节点是否为空,如果为空则返回0。随后创建一个栈,将根节点压入栈中。在循环中,不断取出栈顶元素,交换其左右子树,并将存在的左子树和右子树压入栈中。当栈为空时,所有节点都已经遍历并翻转,返回根节点完成翻转操作
迭代代码:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return 0; // 若根节点为空,则返回0stack<TreeNode*> st; // 创建一个栈用于存储待处理节点st.push(root); // 将根节点入栈while (!st.empty()) { // 当栈不为空时TreeNode* node = st.top(); // 获取栈顶元素st.pop(); // 弹出栈顶元素swap(node->left, node->right); // 交换当前节点的左右子树if (node->left) st.push(node->left); // 如果左子树不为空,则将其入栈if (node->right) st.push(node->right); // 如果右子树不为空,则将其入栈}return root; // 返回翻转后的树的根节点}
};2对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:

输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:

输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
思路:
判断一个二叉树是否对称时,有以下几种情况需要考虑:
-
根节点为空:如果根节点为空,则二叉树被视为对称的,因为空树被认为是对称的。
-
左右节点为空情况:当左节点为空而右节点不为空,或者左节点不为空而右节点为空时,这种情况下两个节点不对称。
-
节点值不相等:如果左右节点的值不相等,那么这两个节点不对称。
-
子树不对称:如果左节点的左子树与右节点的右子树不对称,或者左节点的右子树与右节点的左子树不对称,那么这两个节点也不对称。
代码:
class Solution {
public:// 递归函数,用于比较左右子树是否对称bool compare(TreeNode* left, TreeNode* right) {// 首先排除空节点的情况if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;// 排除了空节点,再排除数值不相同的情况else if (left->val != right->val) return false;// 此时左右节点都不为空,且数值相同的情况,继续递归判断子树bool outside = compare(left->left, right->right); // 左子树的左节点和右子树的右节点比较bool inside = compare(left->right, right->left); // 左子树的右节点和右子树的左节点比较bool isSame = outside && inside; // 判断是否对称return isSame; // 返回结果}// 主函数,判断整棵树是否对称bool isSymmetric(TreeNode* root) {if (root == NULL) return true; // 空树也算对称return compare(root->left, root->right); // 调用递归函数比较左右子树}
}3二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:

输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
递归思路:
-
etdepth函数:用于计算树的深度。若根节点为空,则深度为0;否则分别递归计算左子树和右子树的深度,并取其中较大的深度加1作为当前节点的深度。 -
maxDepth函数:是主函数,直接调用getdepth函数计算二叉树的最大深度,并返回结果。
递归代码:
class Solution {
public:// 递归函数,用于计算树的深度int getdepth(TreeNode* root) {if (root == NULL) return 0; // 如果根节点为空,深度为0int leftdepth = getdepth(root->left); // 递归获取左子树的深度int rightdepth = getdepth(root->right); // 递归获取右子树的深度int depth = 1 + max(leftdepth, rightdepth); // 当前节点的深度为左右子树深度的最大值加1return depth; // 返回当前节点的深度}// 主函数,获取二叉树的最大深度int maxDepth(TreeNode* root) {return getdepth(root); // 调用计算深度的递归函数}
};迭代思路:
-
首先判断根节点是否为空,若为空则直接返回深度为0。
-
创建一个队列 que 存储节点,并将根节点放入队列。
-
进入循环,每次循环代表遍历一层节点,增加深度。
-
遍历当前层的节点,取出队首节点,如果存在左子节点,则将左子节点入队;如果存在右子节点,则将右子节点入队。
-
继续循环直到队列为空,返回最大深度。
迭代代码:
class Solution {
public:// 计算二叉树的最大深度int maxDepth(TreeNode* root) {if (root == nullptr) return 0; // 如果根节点为空,深度为0int maxDepth = 0; // 初始化最大深度为0queue<TreeNode*> que; // 创建一个队列存储节点que.push(root); // 根节点入队while (!que.empty()) { // 当队列不为空时循环int size = que.size(); // 获取当前队列的大小,即当前层节点数maxDepth++; // 对应深度加1for (int i = 0; i < size; i++) {TreeNode* node = que.front(); // 取出队首节点que.pop(); // 队首节点出队if (node->left) que.push(node->left); // 如果左子节点存在,将左子节点入队if (node->right) que.push(node->right); // 如果右子节点存在,将右子节点入队}}return maxDepth; // 返回二叉树的最大深度}
};

)









--王丁丁)

)


![[论文阅读] ZeRo](http://pic.xiahunao.cn/[论文阅读] ZeRo)

