笔记来源：
1.【传送门】
2.【传送门】
前沿原理介绍
Grander因果检验是一种分析时间序列数据因果关系的方法。
基本思想在于，在控制Y的滞后项 (过去值) 的情况下，如果X的滞后项仍然有助于解释Y的当期值的变动，则认为 X对 Y产生因果影响。
操作与解释
基于stata实现
-
准备的数据是时间序列数据。
-
-
命令
1.var y x,lag(1)第一步2.
vargranger第二步
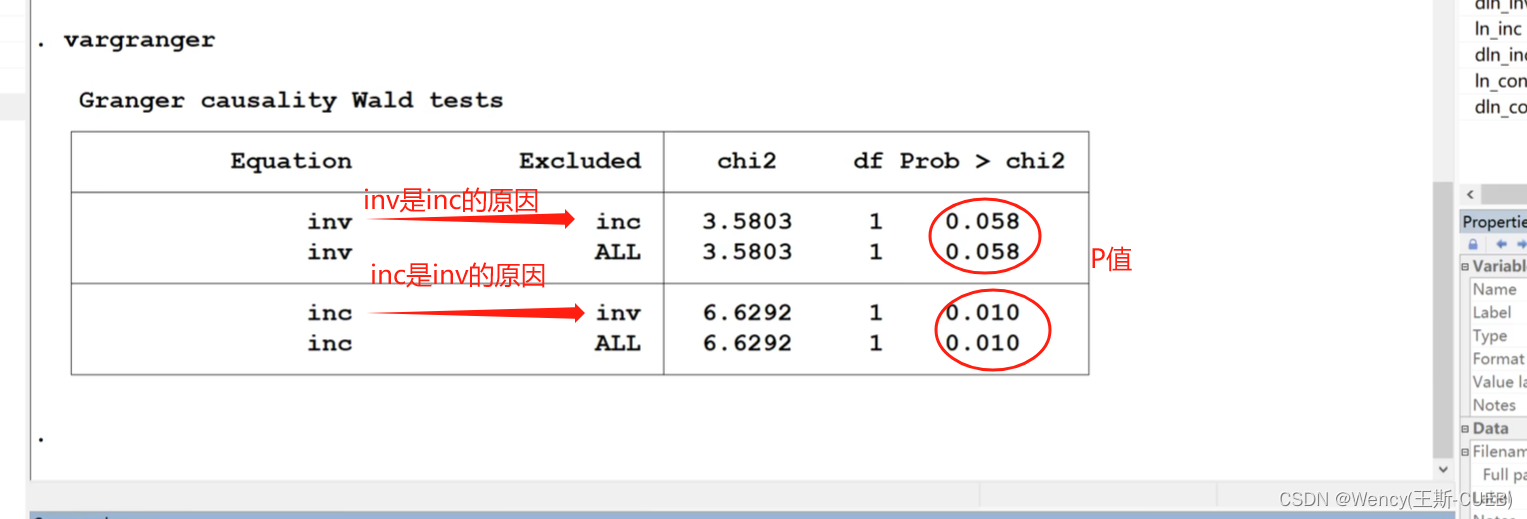
故结果是双向因果
缺陷
-
关联与因果之间的区别： Granger因果检验只能检测到变量之间的时间序列关联关系，而不能确定这种关系的方向。即使Granger因果检验显示两个变量之间存在因果关系，这并不意味着其中一个变量的变化导致了另一个变量的变化，因为Granger因果检验无法解释这种关系的机制。
-
滞后阶数的选择： Granger因果检验中需要选择滞后阶数（lag order），即用多少期的滞后值作为因果关系的判断依据。不同的滞后阶数可能导致不同的结果，而选择合适的滞后阶数通常需要依赖经验或其他理论依据，这可能引入主观因素。
-
小样本效应： 在小样本情况下，Granger因果检验的统计功效较低，可能难以检测到真实的因果关系。因此，在小样本情况下，结果的解释应该更加谨慎。
-
外生变量未控制： Granger因果检验通常假设没有未观测到的外生变量影响被考察的两个变量，如果存在未观测到的外生变量，Granger因果检验的结果可能受到影响。
-
时间变化的影响： Granger因果检验的结果可能受到时间趋势和季节性等时间变化的影响，如果这些因素没有被适当地控制，可能导致因果关系的误判。
-
方向性的局限性： Granger因果关系并不表示因果关系的方向。两个变量相互Granger因果并不意味着它们之间的因果关系是单向的。
-
线性关系的假设： Granger因果检验基于线性关系的假设，可能无法捕捉非线性关系的因果关系。
)
