文章目录
- 堆
- 前言
- 基本介绍
- 认识堆
- 堆的特点
- 堆的分类
- 堆的操作
- 堆的常见应用
- 堆的实现
- JDK 自带的堆
- 手动实现堆
堆
前言
本文主要是对堆的一个简单介绍,如果你是刚学数据结构的话,十分推荐看这篇文章,通过本文你将对堆这个数据结构有一个大致的了解,同时学习JDK自带的堆实现类
PriorityQueue类,如何基于数组手写一个堆。
基本介绍
认识堆
-
什么是堆?
堆(Heap)是一种常见的数据结构,堆可以基于数组实现,也可以基于链表实现。堆的定义如下:n个元素的序列 { k 1 , k 2 , k i , … , k n } {\{k1,k2,ki,…,kn\}} {k1,k2,ki,…,kn} 当且仅当满足下关系 ( k i < = k 2 i , k i < = k 2 i + 1 ) (ki <= k2i,ki <= k2i+1) (ki<=k2i,ki<=k2i+1)或者 ( k i > = k 2 i , k i > = k 2 i + 1 ) , ( i = 1 , 2 , 3 , 4... n / 2 ) (ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2) (ki>=k2i,ki>=k2i+1),(i=1,2,3,4...n/2)时,称之为堆。堆是具备完全二叉树的特点的,二叉堆就是一种特别的完全二叉树,多叉堆也具有完全二叉树的特点。
备注:完全二叉树的特点是,除了最后一层,其他层的叶子节点都是满的,也就是非最后一层节点的度要么是2要么是0,这个度是就是子节点的个数,堆也是具有这个特点的
以下是一些常见的堆:
-
最大堆:父节点永远是最大的,顶点为堆中最大元素
9/ \7 8/ \ / \6 5 2 3/ \ 1 4 -
最小堆:父节点永远是最小的,顶点为堆中最小元素
0/ \1 2/ \ / \6 5 7 3/ \ 9 8/ 4 -
多叉堆:
0/ / \ \/ / \ \2 3 4 5/ | \ 6 7 8
堆的特点
- 堆的特点
- 类完全二叉树:堆具有完全二叉树的特点,除了最后一层外,其他层的节点都是满的,并且最后一层的节点从左到右连续排列。
- 堆序性质:堆中的每个节点都满足堆序性质。对于最小堆来说,任意节点的值都小于等于其子节点的值;而对于最大堆来说,任意节点的值都大于等于其子节点的值。
- 根节点存储极值:在最小堆中,根节点存储着堆中的最小值;而在最大堆中,根节点存储着堆中的最大值。因此,可以通过堆的根节点快速获取极值。
- 快速插入和删除:堆支持高效的插入和删除操作。在最小堆中,插入新元素和删除最小元素的时间复杂度均为 O(log n),其中 n 是堆中元素的数量。最大堆的插入和删除最大元素操作也具有相同的时间复杂度。
堆的分类
- 堆的分类?
- 按照结构可以分为
- 二叉堆:每个节点最多有两个子节点的堆。二叉堆分为最大堆和最小堆。
- 多叉堆:每个节点可以拥有多个子节点的堆,其中特别常见的是二叉堆的扩展,也就是三叉堆、四叉堆等。
- 按照顺序可以分为
- 最大堆:在最大堆中,父节点的值大于或等于其子节点的值。堆顶元素是最大值。
- 最小堆:在最小堆中,父节点的值小于或等于其子节点的值。堆顶元素是最小值。
- 按照结构可以分为
所以也可以组合命名,比如:多叉最小堆、多叉最大堆、二叉最小堆、二叉最大堆,其中最为常见的就是二叉最大堆(一般直接简称最大堆)和二叉最小堆(一般直接简称最小堆),而本文中的堆实现就是主要讲解 最大堆 和 最小堆
堆的操作
- 插入元素:将一个新元素插入到堆中。插入操作通常是在堆的末尾添加新元素,然后通过上浮操作(Heapify Up)或下浮操作(Heapify Down)调整堆的结构,以满足堆的性质。
- 删除元素:从堆中删除指定元素。通常情况下,需要删除的元素是位于堆的根节点。删除操作会将根节点与最后一个叶子节点交换,然后通过下沉操作(Heapify Down)调整堆的结构,以满足堆的性质。
- 获取极值:获取堆中的最大值或最小值(取决于是最大堆还是最小堆)。在最大堆中,最大值存储在根节点;在最小堆中,最小值存储在根节点。获取极值操作可以在 O(1) 的时间复杂度内完成。
- 堆化:通过上浮操作或下沉操作,调整堆的结构,使之满足堆的性质。上浮操作用于维护插入元素后的堆性质,而下沉操作用于维护删除元素后的堆性质。
- 构建堆:将一个无序数组转换为堆的过程。构建堆的常见方法是从数组最后一个非叶子节点开始,依次进行下沉操作,以保证每个节点都满足堆的性质。
-
堆的上浮和下浮操作
-
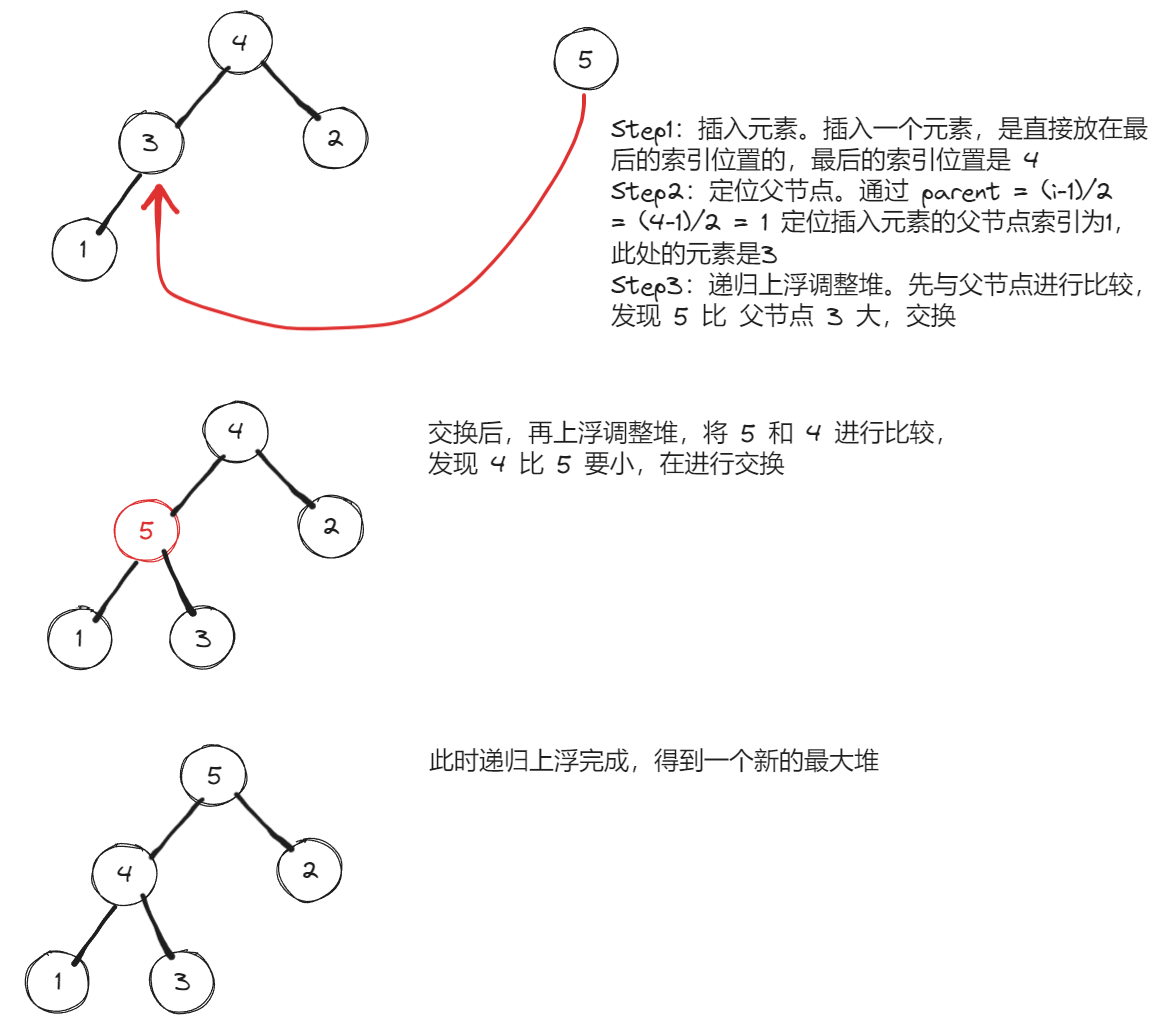
上浮(Heapify Up):也称为向上调整或上升,是指在插入元素到堆时将其移动到正确的位置以满足堆的性质。对于最大堆来说,上浮操作是将新插入的元素不断与其父节点进行比较和交换,直到满足堆的性质。具体步骤如下:
- Step1:将新插入的元素放在堆数组的末尾。
- Step2:将该元素与父节点进行比较,如果它比父节点大(对于最大堆),则交换两者位置。
- Step3:重复上述比较和交换的过程,直到新插入的元素达到合适的位置或成为根节点。
上浮操作保证了插入后的堆仍然保持堆的性质,即对于最大堆,父节点的值大于等于子节点的值。
-
下沉(Heapify Down):也称为向下调整或下降,是指在删除堆顶元素后,将最后一个元素移到堆顶并将其下沉到正确的位置以满足堆的性质。对于最大堆来说,下沉操作是将堆顶元素不断与其子节点进行比较和交换,直到满足堆的性质。具体步骤如下:
- Step1:将堆数组的最后一个元素移到堆顶位置。
- Step2:将堆顶元素与它的子节点进行比较,选择较大的子节点。
- Step3:如果堆顶元素小于较大的子节点(对于最大堆),则交换两者位置。
- Step4:重复上述比较和交换的过程,直到堆顶元素达到合适的位置或成为叶子节点。
下沉操作保证了删除堆顶元素后的堆仍然保持堆的性质,即对于最大堆,父节点的值大于等于子节点的值。

-
堆的常见应用
基于堆的特点,堆的常见应用有:
- 优先队列(Priority Queue):堆常被用于实现优先队列,其中元素按照优先级进行排序。通过堆的性质,可以快速插入新元素和获取当前最高优先级的元素。
- 堆排序(Heap Sort):堆排序是一种基于堆的排序算法,它利用堆的属性进行排序。堆排序是一种原地、稳定的排序算法,具有较好的平均和最坏时间复杂度,适用于大规模数据集的排序。
- 图算法中的最短路径和最小生成树:堆被广泛用于图算法中的最短路径和最小生成树问题。例如,Dijkstra算法使用最小堆来选择下一个距离顶点最短的节点,Prim算法使用最小堆来选择下一个距离树最近的边。
- 模拟系统中的事件调度:在模拟系统中,堆可用于事件驱动的调度和处理。每个事件都具有优先级,堆的结构使得可以快速找到下一个最高优先级的事件进行处理。
- 中位数的查找:通过使用两个堆,分别维护数据流的较小部分和较大部分,可以高效地查找中位数。
- 数据压缩和哈夫曼编码:堆可用于构建哈夫曼树,用于数据压缩和编码。根据字符频率构建最小堆,然后按照频率合并节点,生成哈夫曼树,并将字符编码为可变长度的前缀码。
堆的实现
JDK 自带的堆
在Java中,有一个名为PriorityQueue的类实现了堆(Heap)的功能。PriorityQueue是一个优先队列,基于堆的数据结构实现。
使用PriorityQueue可以方便地操作堆的插入、删除和获取极值等操作。它根据元素的优先级进行排序,并保证每次操作都能够高效地获取最高优先级的元素。
以下是一些PriorityQueue常用方法的示例:
add(E e)或offer(E e):网堆中添加元素。将元素插入优先队列。remove()或poll():删除堆的根节点。删除并返回队列中的最高优先级元素。peek():获取极值。返回队列中的最高优先级元素,但不删除。size():获取堆中元素的数量。返回队列中的元素个数。
至于堆化和构建堆的操作 JDK 底层自动实现了,我们只管调用无需关心实现,这就是 Java 的好处吧
备注:PriorityQueue默认是最小堆(小顶堆),即优先级较低的元素具有更高的优先级。如果需要使用最大堆(大顶堆),可以通过提供自定义的Comparator来实现。
示例
示例一:最小堆(默认)
堆顶元素永远是最小的
import java.util.PriorityQueue;public class HeapExample {public static void main(String[] args) {PriorityQueue<Integer> minHeap = new PriorityQueue<>();minHeap.add(5);minHeap.add(2);minHeap.add(8);System.out.println(minHeap.peek()); // 输出: 2System.out.println(minHeap.poll()); // 输出: 2System.out.println(minHeap.peek()); // 输出: 5System.out.println(minHeap.size()); // 输出: 2}
}
示例二:最大堆
堆顶元素永远是最大的
import java.util.Comparator;
import java.util.PriorityQueue;public class MaxHeapExample {public static void main(String[] args) {PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());maxHeap.add(5);maxHeap.add(2);maxHeap.add(8);System.out.println(maxHeap.peek()); // 输出: 8System.out.println(maxHeap.poll()); // 输出: 8System.out.println(maxHeap.peek()); // 输出: 5System.out.println(maxHeap.size()); // 输出: 2}
}
手动实现堆
注意:以下实现都是基于数组实现的,基于链表实现的我就没有写了,一般而言堆都是基于数组实现的,因为数组相对链表,内存是连续的,不需要存引用,相较而言,查询性能更好,内存占用也会相对少很多
手写堆提供的API
-
Heap():创建堆的无参构造方法,默认容量为10 -
Heap(int capacity):创建堆的有参构造方法,指定堆的初始容量 -
add(int val):往堆中添加一个元素,超过容量会自动进行扩容,扩容为原来容量的两倍 -
remove():移除并返回堆顶的元素(也就是极大值) -
remove(int val):移除指定元素并返回,如果不存在抛异常 -
printHeap():打印堆中的元素,相当于是层序遍历二叉树 -
isEmpty():判断堆是否为空
/*** @author ghp* @title* @description*/
public class Heap {/*** 堆的默认容量*/private static final int DEFAULT_CAPACITY = 10;/*** 堆数组,用于存储堆中的元素*/private int[] heapArray;/*** 堆的容量*/private int capacity;/*** 堆中元素的数量*/private int size;public Heap() {this.capacity = DEFAULT_CAPACITY;this.heapArray = new int[capacity];this.size = 0;}public Heap(int capacity) {this.capacity = capacity;this.heapArray = new int[capacity];this.size = 0;}/*** 遍历打印堆中所有的元素*/public void printHeap() {for (int i = 0; i < size; i++) {System.out.print(heapArray[i] + " ");}System.out.println();}/*** 判断堆是否为空** @return*/public boolean isEmpty() {return size == 0;}/*** 往队中添加一个元素** @param value*/public void add(int value) {if (size == capacity) {// 扩容为当前容量的两倍resize(capacity * 2);}heapArray[size] = value;heapifyUp(size++);}/*** 移除堆顶元素** @return*/public int remove() {if (isEmpty()) {throw new IllegalStateException("Heap is empty");}int max = heapArray[0];heapArray[0] = heapArray[--size];heapifyDown(0);return max;}/*** 移除堆中指定元素** @param value*/public void remove(int value) {int index = findIndex(value);if (index == -1) {throw new IllegalArgumentException("Element does not exist in the heap");}// 使用最后一个节点覆盖要删除的元素,这样才能确保节点都能进行一个更新heapArray[index] = heapArray[--size];heapifyDown(index);}/*** 寻找到指定元素的索引** @param value* @return*/private int findIndex(int value) {for (int i = 0; i < size; i++) {if (heapArray[i] == value) {return i;}}return -1;}/*** 上浮(新增操作时节点上移)** @param index*/private void heapifyUp(int index) {// 定位父节点int parent = (index - 1) / 2;if (parent >= 0 && heapArray[parent] < heapArray[index]) {// 如果父节点比子节点小,则进行交换,然后递归上浮,确保父节点是永远大于子节点的swap(parent, index);heapifyUp(parent);}}/*** 下浮(删除操作时节点下移)** @param index*/private void heapifyDown(int index) {// 左节点的索引int left = 2 * index + 1;// 右节点的索引int right = 2 * index + 2;// 父节点索引int parent = index;// 判断左右节点是否大于父节点if (left < size && heapArray[left] > heapArray[parent]) {parent = left;}if (right < size && heapArray[right] > heapArray[parent]) {parent = right;}if (parent != index) {// 如果父节点发生了更新,则交换父节点和子节点的位置,同时递归下浮,确保父节点永远是最大的swap(parent, index);heapifyDown(parent);}}/*** 交换堆数组索引为 i 和 j 的两个元素** @param i* @param j*/private void swap(int i, int j) {int temp = heapArray[i];heapArray[i] = heapArray[j];heapArray[j] = temp;}/*** 扩容堆大小** @param newCapacity*/private void resize(int newCapacity) {if (newCapacity < DEFAULT_CAPACITY){newCapacity = DEFAULT_CAPACITY;}if (newCapacity < 0) {newCapacity = Integer.MAX_VALUE;}heapArray = Arrays.copyOf(heapArray, newCapacity);capacity = newCapacity;}
}
备注:如果想要使用最小堆,则只需要修改上浮和下浮的if判断条件即可
测试:
public class Test {public static void main(String[] args) {Heap heap = new Heap(0);heap.add(1);heap.add(2);heap.add(3);heap.add(4);heap.add(5);heap.printHeap();heap.remove(1);heap.printHeap();}
}


)


)

)

代码示例java)
----归并排序)
)

+复制可用))




——添加手柄摇杆控制移动)

