希尔排序

希尔排序与插入排序原理相同，希尔排序是一种分组插入排序算法

> 首先取一个整数d1=n/2，将元素分为d1个组，每组相邻两元素之间距离为d1，在各组内之间插入排序。

> 取第二个整数d2=n/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内直接插入排序

> 希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使所有数据有序。

给一个数组：5，7，4，6，3，1，2，9，8

首先d=4:

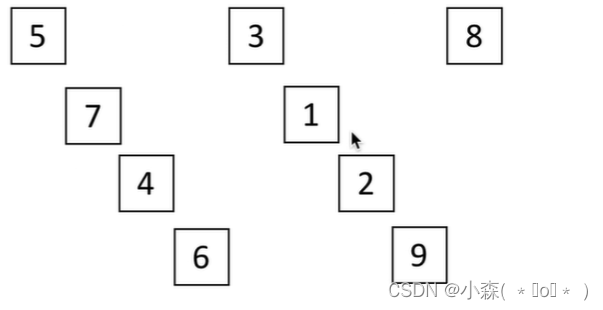
5和3交换位置；7和1交换位置；4和2交换位置；6和9位置不变；

数组在第一轮变为3，1，2，6，5，7，4，9，8

然后d=2:

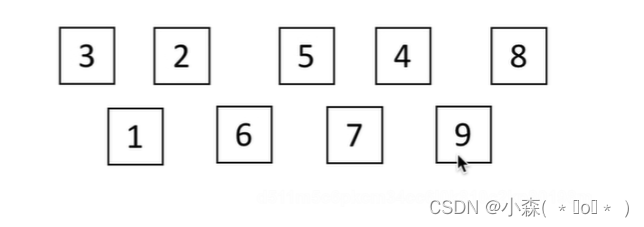
两组内部再次插入排序，结果变为2，1，3，6，4，7，5，9，8

最后d=1，整体插入排序使数组有序：1，2，3，4，5，6，7，8，9

> 希尔排序代码：

def insert_sort_gap(li,gap):for i in range(gap,len(li)):  # i 表示摸到牌的下标tmp=li[i]j=i-gapwhile j>=0 and li[j]>tmp:li[j+gap]=li[j]j-=gapli[j+gap]=tmpdef shell_sort(li):d=len(li) //2while d>=1:insert_sort_gap(li,d)d //=2

计数排序

计数排序是对列表进行排序，列表中的数大小在0到100之间，时间复杂度为O(n)

对于一个数组，我们先写出一个从0到5的数，然后在这些数后边写上每个值在列表中出现的次数

我们在整个数组中先写出这些统计的值的数默认为0

我们找出出现的次数后：

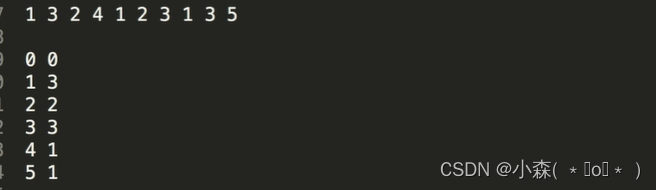
将其按大小写出：1，1，1，2，2，3，3，3，4，5

> 希尔排序代码：

def count_sort(li,max_count=100):count=[0 for _ in range(max_count+1)]   #生成100个0，他们的下标就是列表中的值for val in li:count[val] +=1li.clear()for ind,val in enumerate(count):for i in range(val):                #添加整个值的次数为valli.append(ind)