CORDIC 算法实现 _FPGA

注：本文为 “CORDIC 算法” 相关文章合辑。

未整理去重。

如有内容异常，请看原文。

Cordic 算法的原理介绍

乐富道 2014-01-28 23:05

Cordic 算法知道正弦和余弦值，求反正切，即角度。

采用用不断的旋转求出对应的正弦余弦值，是一种近似求解发。

旋转的角度很讲求，每次旋转的角度必须使得 正切值近似等于 1 2 N \frac{1}{2^N} 2N1​。旋转的目的是让 Y Y Y 轴趋近与 0 0 0。把每次旋转的角度累加，即得到旋转的角度和即为正切值。

比如 Y Y Y 轴旋转 4 5 ∘ 45^{\circ} 45∘，则值减小 1 2 \frac{1}{2} 21​;

再旋转 26.5650 5 ∘ 26.56505^{\circ} 26.56505∘，再减少 1 4 \frac{1}{4} 41​;

再旋转角度 14.0362 4 ∘ 14.03624^{\circ} 14.03624∘，再减少 1 8 \frac{1}{8} 81​; 依次减少 1 16 \frac{1}{16} 161​， 1 32 ⋯ ⋯ \frac{1}{32}\cdots\cdots 321​⋯⋯，最后 Y Y Y 轴的值无限小，趋近于 0 0 0 。

比如 X = 1 X = 1 X=1， Y = 1 Y = 1 Y=1，的角度，角度是 4 5 ∘ 45^{\circ} 45∘。经过一次旋转，要使得 Y = 0 Y = 0 Y=0，这个角度必须是 4 5 ∘ 45^{\circ} 45∘。

img

如上图

img

如图中，直角坐标系中点（ X 0 X_0 X0​， Y 0 Y_0 Y0​）逆时钟旋转角度 θ \theta θ，变换成坐标（ X 1 X_1 X1​， Y 1 Y_1 Y1​）,那么用 X 0 X_0 X0​， Y 0 Y_0 Y0​,以及 θ \theta θ 的三角函数，如果表示 X 1 X_1 X1​， Y 1 Y_1 Y1​ 呢？

img

请想象，如果坐标也旋转角度 θ \theta θ，那么 X 1 X_1 X1​， Y 1 Y_1 Y1​ 的坐标依然是( X 0 X_0 X0​， Y 0 Y_0 Y0​)。接着往下看：

img

看完以上这副图，就该明白这个等式了：

x 1 = x 0 cos ⁡ θ − y 0 sin ⁡ θ x_1 = x_0\cos\theta - y_0\sin\theta x1​=x0​cosθ−y0​sinθ

y 1 = x 0 sin ⁡ θ + y 0 cos ⁡ θ y_1 = x_0\sin\theta + y_0\cos\theta y1​=x0​sinθ+y0​cosθ

再把这个式子化成正切函数。

img

Cordic 算法的思想是通过迭代的方法，不断的旋转特定的角度(这个特定的角度就是使得 Y Y Y 为上次的 1 2 \frac{1}{2} 21​)，使得累计旋转的角度的和无限接近某一设定的角度，

每次旋转的角度的 θ = arctan ⁡ ( 1 2 n ) \theta = \arctan(\frac{1}{2^n}) θ=arctan(2n1​)；

img

具体迭代如下表： Z 0 = 3 0 ∘ Z_0 = 30^{\circ} Z0​=30∘， Y 0 = 0 Y_0 = 0 Y0​=0， X 0 = 0.6073 X_0 = 0.6073 X0​=0.6073

输入 3 0 ∘ 30^{\circ} 30∘，经过 9 9 9 次迭代后， Z 0 = 0 Z_0 = 0 Z0​=0， Y 0 = 0.5006 Y_0 = 0.5006 Y0​=0.5006， X 0 = 0.8657 X_0 = 0.8657 X0​=0.8657

img

x ( i + 1 ) ′ = ( x i ′ − y i ′ ( σ i ) 2 − i ) x'_{(i + 1)} = (x'_i - y'_i(\sigma_i)2^{-i}) x(i+1)′​=(xi′​−yi′​(σi​)2−i)

y ( i + 1 ) ′ = ( x i ′ ( σ i ) 2 − i + y i ′ ) y'_{(i + 1)} = (x'_i(\sigma_i)2^{-i} + y'_i) y(i+1)′​=(xi′​(σi​)2−i+yi′​)

(当 i = 0 i = 0 i=0)

x 1 ′ = 0.607 − 0 ⋅ ( + 1 ) ⋅ 1 = 0.607 x'_1 = 0.607 - 0 \cdot (+1 ) \cdot 1 = 0.607 x1′​=0.607−0⋅(+1)⋅1=0.607

y 1 ′ = 0.607 ⋅ ( + 1 ) ⋅ 1 + 0 = 0.607 y'_1 = 0.607 \cdot (+1 ) \cdot 1 + 0 = 0.607 y1′​=0.607⋅(+1)⋅1+0=0.607

通过 Cordic 算法后，得到

y 9 = 0.5006 ( = sin ⁡ ( 3 0 ∘ ) ) y_9 = 0.5006 (=\sin(30^{\circ})) y9​=0.5006(=sin(30∘))

x 9 = 0.8657 ( = cos ⁡ ( 3 0 ∘ ) ) x_9 = 0.8657 (=\cos(30^{\circ})) x9​=0.8657(=cos(30∘))

所以也可以用 cordic 算法求出正切值的。

或者求反正切值：

img

计算公式：

img

posted @ 2014-01-28 23:05 乐富道

基于 FPGA 的 CORDIC 算法实现 —— Verilog 版

善良的一休君于 2017-08-21 20:07:34 发布

目前，学习与开发 FPGA 的程序员们大多使用的是 Verilog HDL 语言（以下简称为 Verilog），关于 Verilog 的诸多优点一休哥就不多介绍了，在此，我们将重点放在 Verilog 的运算操作上。

我们都知道，在 Verilog 中，运算一般分为逻辑运算（与或非等）与算术运算（加减乘除等）。而在一开始学习 Verilog 时，老司机一定会提醒我们，“切记，千万别用‘/’除、‘%’取模（有的也叫取余）和‘**’幂。” 这话说的不无道理，因为这三个运算是不可综合的。但，需清楚理解的是，不可综合的具体意思为不能综合为简单的模块，当我们在程序中调用了这些运算时，‘/’除和‘%’取模在 Quartus 软件中是可以综合的，因此可以正常调用运行，但是会消耗一些逻辑资源，而且会产生延时，即这两个运算的处理时间会很长，可能会大于时序控制时钟的单周期时间。此时呢，我们会建议你调用 IP 核来实现运算操作，虽然这样也会消耗许多逻辑资源，但产生的延时相对较小满足了你基本的需求。

问题好像迎刃而解了，可是仔细一想，除了这些运算，我们还剩下什么？对呀，三角函数，反三角函数，对数函数，指数函数呢，这些函数我们在高中就学习了的呀，难道在 FPGA 中就没有用武之地吗？有人会说，查找表呗，首先将某个运算的所有可能的输入与输出对一一罗列出来，然后放进 Rom 中，然后根据输入查表得到输出。这个方法虽然有效的避免了延时问题，却是一个十分消耗资源的方法，不适合资源紧张的设计。那么，就真的没有办法了吗？

答案就是咱们今天的标题了，CORDIC，而且 CORDIC 是一个比较全能的算法，通过这一原理，我们可以实现三角函数，反三角函数，对数函数，指数函数等多种运算。接下来，一休哥就带领大家来学习 CORDIC 的原理吧。（题外话：请相信一休哥，本文不会让你感到太多痛苦～）

本文将分三个小部分来展开介绍：

1、CORDIC 的基本原理介绍

2、CORDIC 的具体操作流程介绍

3、CORDIC 的旋转模式 ——Verilog 仿真

本文涉及到的全部资料链接：

链接：http://pan.baidu.com/s/1gfrJzMj
密码：x92u

一、CORDIC 的基本原理介绍

CORDIC 算法是一个 “化繁为简” 的算法，将许多复杂的运算转化为一种 “仅需要移位和加法” 的迭代操作。CORDIC 算法有旋转和向量两个模式，分别可以在圆坐标系、线性坐标系和双曲线坐标系使用，从而可以演算出 8 种运算，而结合这 8 种运算也可以衍生出其他许多运算。下表展示了 8 种运算在 CORDIC 算法中实现的条件。

这里写图片描述

这里写图片描述

首先，我们先从旋转模式下的圆坐标系讲起，这也是 CORDIC 方法最初的用途。

1、CORDIC 的几何原理介绍

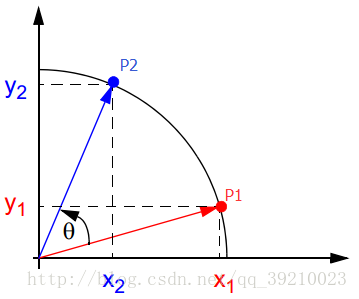
假设在 x y xy xy 坐标系中有一个点 P 1 ( x 1 , y 1 ) P1(x_1,y_1) P1(x1​,y1​)，将 P 1 P1 P1 点绕原点旋转 θ \theta θ 角后得到点 P 2 ( x 2 , y 2 ) P2(x_2,y_2) P2(x2​,y2​)。

这里写图片描述

这里写图片描述

于是可以得到 P 1 P1 P1 和 P 2 P2 P2 的关系：

x 2 = x 1 cos ⁡ θ − y 1 sin ⁡ θ = cos ⁡ θ ( x 1 − y 1 tan ⁡ θ ) y 2 = y 1 cos ⁡ θ + x 1 sin ⁡ θ = cos ⁡ θ ( y 1 + x 1 tan ⁡ θ ) \begin{align*} x_2 &= x_1\cos\theta - y_1\sin\theta = \cos\theta(x_1 - y_1\tan\theta)\\ y_2 &= y_1\cos\theta + x_1\sin\theta = \cos\theta(y_1 + x_1\tan\theta) \end{align*} x2​y2​​=x1​cosθ−y1​sinθ=cosθ(x1​−y1​tanθ)=y1​cosθ+x1​sinθ=cosθ(y1​+x1​tanθ)​

以上就是CORDIC的几何原理部分，而我们该如何深入理解这个几何原理的真正含义呢？

从原理中，我们可以知道，当已知一个点 P 1 P1 P1 的坐标，并已知该点 P 1 P1 P1 旋转的角度 θ \theta θ，则可以根据上述公式求得目标点 P 2 P2 P2 的坐标。然后，麻烦来了，我们需要用FPGA去执行上述运算操作，而FPGA的Verilog语言根本不支持三角函数运算。因此，我们需要对上述式子进行简化操作，将复杂的运算操作转换为一种单一的“迭代位移”算法。那么，接下来我们介绍优化算法部分。

2、CORDIC的优化算法介绍

我们先介绍算法的优化原理：将旋转角 θ \theta θ 细化成若干分固定大小的角度 θ i \theta_i θi​，并且规定 θ i \theta_i θi​ 满足 tan ⁡ θ i = 2 − i \tan\theta_i = 2^{-i} tanθi​=2−i，因此 ∑ θ i \sum\theta_i ∑θi​ 的值在 [ − 99. 7 ∘ , 99. 7 ∘ ] [-99.7^{\circ},99.7^{\circ}] [−99.7∘,99.7∘] 范围内，如果旋转角 θ \theta θ 超出此范围，则运用简单的三角运算操作即可（加减 π \pi π）。

然后我们需要修改几何原理部分的假设，假设在 x y xy xy 坐标系中有一个点 P 0 ( x 0 , y 0 ) P0(x_0,y_0) P0(x0​,y0​)，将 P 0 P0 P0 点绕原点旋转 θ \theta θ 角后得到点 P n ( x n , y n ) Pn(x_n,y_n) Pn(xn​,yn​)。

于是可以得到 P 0 P0 P0 和 P n Pn Pn 的关系：

x n = x 0 cos ⁡ θ − y 0 sin ⁡ θ = cos ⁡ θ ( x 0 − y 0 tan ⁡ θ ) y n = y 0 cos ⁡ θ + x 0 sin ⁡ θ = cos ⁡ θ ( y 0 + x 0 tan ⁡ θ ) \begin{align*} x_n &= x_0\cos\theta - y_0\sin\theta = \cos\theta(x_0 - y_0\tan\theta)\\ y_n &= y_0\cos\theta + x_0\sin\theta = \cos\theta(y_0 + x_0\tan\theta) \end{align*} xn​yn​​=x0​cosθ−y0​sinθ=cosθ(x0​−y0​tanθ)=y0​cosθ+x0​sinθ=cosθ(y0​+x0​tanθ)​

然后，我们将旋转角 θ \theta θ 细化成 θ i \theta_i θi​，由于每次的旋转角度 θ i \theta_i θi​ 是固定不变的（因为满足 tan ⁡ θ i = 2 − i \tan\theta_i = 2^{-i} tanθi​=2−i），如果一直朝着一个方向旋转则 ∑ θ i \sum\theta_i ∑θi​ 一定会超过 θ \theta θ（如果 θ \theta θ 在 [ − 99. 7 ∘ , 99. 7 ∘ ] [-99.7^{\circ},99.7^{\circ}] [−99.7∘,99.7∘] 范围内）。因此我们需要对 θ i \theta_i θi​ 设定一个方向值 d i d_i di​。如果旋转角已经大于 θ \theta θ，则 d i d_i di​ 为 − 1 -1 −1，表示下次旋转为顺时针，即向 θ \theta θ 靠近；如果旋转角已经小于 θ \theta θ，则 d i d_i di​ 为 1 1 1，表示下次旋转为逆时针，即也向 θ \theta θ 靠近。然后我们可以得到每次旋转的角度值 d i θ i d_i\theta_i di​θi​，设角度剩余值为 z i + 1 z_{i + 1} zi+1​，则有 z i + 1 = z i − d i θ i z_{i + 1} = z_i - d_i\theta_i zi+1​=zi​−di​θi​，其中 z 0 z_0 z0​ 为 θ \theta θ。如此随着 i i i 的增大，角度剩余值 z i + 1 z_{i + 1} zi+1​ 将会趋近于 0 0 0，此时运算结束。（注：可以发现， d i d_i di​ 与 z i z_i zi​ 的符号位相同）

第一次旋转 θ 0 \theta_0 θ0​， d 0 d_0 d0​ 为旋转方向：

x 1 = cos ⁡ θ 0 ( x 0 − d 0 y 0 tan ⁡ θ 0 ) y 1 = cos ⁡ θ 0 ( y 0 + d 0 x 0 tan ⁡ θ 0 ) \begin{align*} x_1 &= \cos\theta_0(x_0 - d_0y_0\tan\theta_0)\\ y_1 &= \cos\theta_0(y_0 + d_0x_0\tan\theta_0) \end{align*} x1​y1​​=cosθ0​(x0​−d0​y0​tanθ0​)=cosθ0​(y0​+d0​x0​tanθ0​)​

第二次旋转 θ 1 \theta_1 θ1​， d 1 d_1 d1​ 为旋转方向：

x 2 = cos ⁡ θ 1 ( x 1 − d 1 y 1 tan ⁡ θ 1 ) = cos ⁡ θ 1 cos ⁡ θ 0 ( x 0 − d 0 y 0 tan ⁡ θ 0 − d 1 y 0 tan ⁡ θ 1 − d 1 d 0 x 0 tan ⁡ θ 1 tan ⁡ θ 0 ) y 2 = cos ⁡ θ 1 ( y 1 + d 1 x 1 tan ⁡ θ 1 ) = cos ⁡ θ 1 cos ⁡ θ 0 ( y 0 + d 0 x 0 tan ⁡ θ 0 + d 1 x 0 tan ⁡ θ 1 − d 1 d 0 y 0 tan ⁡ θ 1 tan ⁡ θ 0 ) \begin{align*} x_2 &= \cos\theta_1(x_1 - d_1y_1\tan\theta_1)\\ &= \cos\theta_1\cos\theta_0(x_0 - d_0y_0\tan\theta_0 - d_1y_0\tan\theta_1 - d_1d_0x_0\tan\theta_1\tan\theta_0)\\ y_2 &= \cos\theta_1(y_1 + d_1x_1\tan\theta_1)\\ &= \cos\theta_1\cos\theta_0(y_0 + d_0x_0\tan\theta_0 + d_1x_0\tan\theta_1 - d_1d_0y_0\tan\theta_1\tan\theta_0) \end{align*} x2​y2​​=cosθ1​(x1​−d1​y1​tanθ1​)=cosθ1​cosθ0​(x0​−d0​y0​tanθ0​−d1​y0​tanθ1​−d1​d0​x0​tanθ1​tanθ0​)=cosθ1​(y1​+d1​x1​tanθ1​)=cosθ1​cosθ0​(y0​+d0​x0​tanθ0​+d1​x0​tanθ1​−d1​d0​y0​tanθ1​tanθ0​)​

大家可能已经发现了，在我们旋转的过程中，式子里一直会有 tan ⁡ θ i \tan\theta_i tanθi​ 和 cos ⁡ θ i \cos\theta_i cosθi​，而每次都可以提取出 cos ⁡ θ i \cos\theta_i cosθi​。虽然我们的FPGA无法计算 tan ⁡ θ i \tan\theta_i tanθi​，但我们知道 tan ⁡ θ i = 2 − i \tan\theta_i = 2^{-i} tanθi​=2−i，因此可以执行和 tan ⁡ θ i \tan\theta_i tanθi​ 效果相同的移位操作 2 − i 2^{-i} 2−i 来取代 tan ⁡ θ i \tan\theta_i tanθi​。而对于 cos ⁡ θ i \cos\theta_i cosθi​，我们可以事先全部提取出来，然后等待迭代结束之后（角度剩余值 z i + 1 z_{i + 1} zi+1​ 趋近于 0 0 0，一般当系统设置最大迭代次数为 16 16 16 时 z i + 1 z_{i + 1} zi+1​ 已经很小了），然后计算出 ∏ i = 0 n − 1 cos ⁡ θ i \prod_{i = 0}^{n - 1}\cos\theta_i ∏i=0n−1​cosθi​ 的值即可。

总结一下：

迭代公式有三：

x i + 1 = x i − d i y i 2 − i (提取了 cos ⁡ θ i , 2 − i 等效替换了 tan ⁡ θ i 之后) y i + 1 = y i + d i x i 2 − i (提取了 cos ⁡ θ i , 2 − i 等效替换了 tan ⁡ θ i 之后) z i + 1 = z i − d i θ i \begin{align*} x_{i + 1} &= x_i - d_iy_i2^{-i} \quad \text{(提取了}\cos\theta_i, 2^{-i}\text{等效替换了}\tan\theta_i\text{之后)}\\ y_{i + 1} &= y_i + d_ix_i2^{-i} \quad \text{(提取了}\cos\theta_i, 2^{-i}\text{等效替换了}\tan\theta_i\text{之后)}\\ z_{i + 1} &= z_i - d_i\theta_i \end{align*} xi+1​yi+1​zi+1​​=xi​−di​yi​2−i(提取了cosθi​,2−i等效替换了tanθi​之后)=yi​+di​xi​2−i(提取了cosθi​,2−i等效替换了tanθi​之后)=zi​−di​θi​​

其中 i i i 从 0 0 0 开始迭代，假设当 i = n − 1 i = n - 1 i=n−1 时， z n z_n zn​ 趋近于 0 0 0，迭代结束。然后对结果乘上 ∏ i = 0 n − 1 cos ⁡ θ i \prod_{i = 0}^{n - 1}\cos\theta_i ∏i=0n−1​cosθi​，于是得到点 P n ( x n ∏ i = 0 n − 1 cos ⁡ θ i , y n ∏ i = 0 n − 1 cos ⁡ θ i ) Pn(x_n\prod_{i = 0}^{n - 1}\cos\theta_i,y_n\prod_{i = 0}^{n - 1}\cos\theta_i) Pn(xn​∏i=0n−1​cosθi​,yn​∏i=0n−1​cosθi​)，此时的点 P n Pn Pn 就近似等于之前假设中的点 P n ( x n , y n ) Pn(x_n,y_n) Pn(xn​,yn​) 了，所以此时的点 P n Pn Pn 同样满足之前假设得到的公式：

x n ∏ i = 0 n − 1 cos ⁡ θ i = x 0 cos ⁡ θ − y 0 sin ⁡ θ y n ∏ i = 0 n − 1 cos ⁡ θ i = y 0 cos ⁡ θ + x 0 sin ⁡ θ \begin{align*} x_n\prod_{i = 0}^{n - 1}\cos\theta_i &= x_0\cos\theta - y_0\sin\theta\\ y_n\prod_{i = 0}^{n - 1}\cos\theta_i &= y_0\cos\theta + x_0\sin\theta \end{align*} xn​i=0∏n−1​cosθi​yn​i=0∏n−1​cosθi​​=x0​cosθ−y0​sinθ=y0​cosθ+x0​sinθ​

由于 i i i 从 0 0 0 至 n − 1 n - 1 n−1，所以上式可以转化成下式：

x n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( x 0 cos ⁡ θ − y 0 sin ⁡ θ ) (其中 i 从 0 至 n − 1 ) y n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( y 0 cos ⁡ θ + x 0 sin ⁡ θ ) (其中 i 从 0 至 n − 1 ) \begin{align*} x_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(x_0\cos\theta - y_0\sin\theta) \quad \text{(其中}i\text{从}0\text{至}n - 1\text{)}\\ y_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(y_0\cos\theta + x_0\sin\theta) \quad \text{(其中}i\text{从}0\text{至}n - 1\text{)} \end{align*} xn​yn​​=∏i=0n−1​cosθi​1​(x0​cosθ−y0​sinθ)(其中i从0至n−1)=∏i=0n−1​cosθi​1​(y0​cosθ+x0​sinθ)(其中i从0至n−1)​

注意：上式中的 x n x_n xn​， y n y_n yn​ 是经过迭代后的结果，而不是之前假设中的点 P n ( x n , y n ) Pn(x_n,y_n) Pn(xn​,yn​)。了解这点是十分重要的。

根据高中学的三角函数关系，可以知道 cos ⁡ θ i = 1 ( 1 + tan ⁡ 2 θ i ) 1 2 = 1 ( 1 + 2 − 2 i ) 1 2 \cos\theta_i = \frac{1}{(1 + \tan^{2}\theta_i)^{\frac{1}{2}}} = \frac{1}{(1 + 2^{-2i})^{\frac{1}{2}}} cosθi​=(1+tan2θi​)21​1​=(1+2−2i)21​1​，而 1 ( 1 + 2 − 2 i ) 1 2 \frac{1}{(1 + 2^{-2i})^{\frac{1}{2}}} (1+2−2i)21​1​ 的极值为 1 1 1，因此我们可以得出一个结论：当 i i i 的次数很大时， ∏ i = 0 n − 1 cos ⁡ θ i \prod_{i = 0}^{n - 1}\cos\theta_i ∏i=0n−1​cosθi​ 的值趋于一个常数。

关于如何计算 ∏ cos ⁡ θ i \prod\cos\theta_i ∏cosθi​ 的代码如下所示：

close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
jiao = zeros(die,1);%每次旋转的角度
cos_value = zeros(die,1);%每次旋转的角度的余弦值
K = zeros(die,1);%余弦值的N元乘积
K_1 = zeros(die,1);%余弦值的N元乘积的倒数
for i = 1 : diea = 2^(-(i-1));jiao(i) = atan(a);cos_value(i) = cos(jiao(i));if( i == 1)K(i) = cos_value(i);K_1(i) = 1/K(i);elseK(i) = K(i-1)*cos_value(i);K_1(i) = 1/K(i);end
end
jiao = vpa(rad2deg(jiao)*256,10) 
cos_value = vpa(cos_value,10)
K = vpa(K,10)
K_1 = vpa(K_1,10)

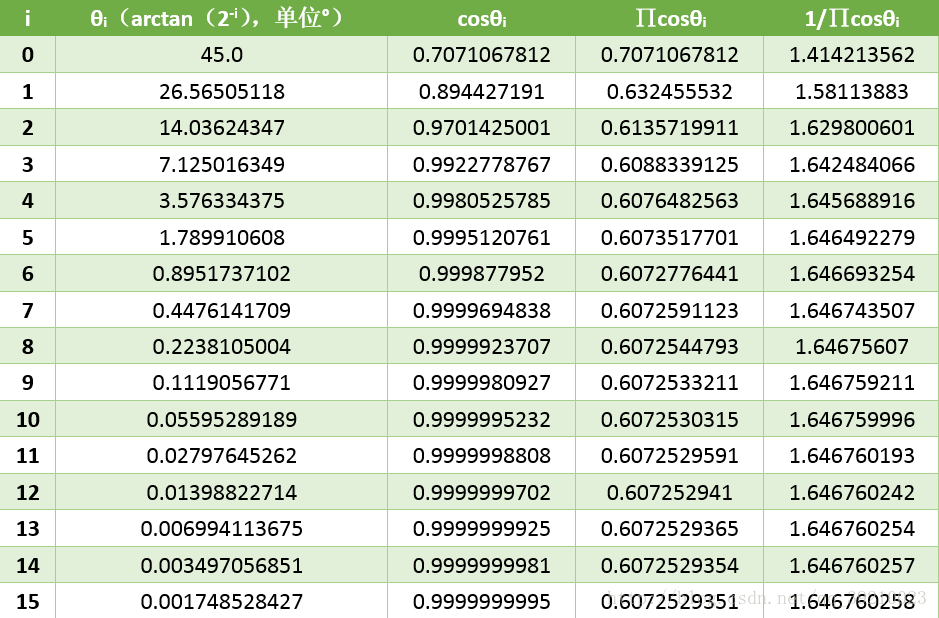
这里写图片描述

这里写图片描述

从上表也可以看出，当迭代次数为 16 16 16， i = 15 i = 15 i=15 时， cos ⁡ θ i \cos\theta_i cosθi​ 的值已经非常趋近于 1 1 1 了， ∏ i = 0 n − 1 cos ⁡ θ i \prod_{i = 0}^{n - 1}\cos\theta_i ∏i=0n−1​cosθi​ 的值则约等于 0.607253 0.607253 0.607253， 1 ∏ i = 0 n − 1 cos ⁡ θ i \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i} ∏i=0n−1​cosθi​1​ 为 1.64676 1.64676 1.64676。所以当迭代次数等于 16 16 16 时，通过迭代得到的点 P n Pn Pn 坐标已经非常接近之前假设中的点 P n Pn Pn。所以，当迭代次数等于 16 16 16 时，这个式子是成立的。

x n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( x 0 cos ⁡ θ − y 0 sin ⁡ θ ) ( 其中  i 从  0 至  n − 1 ) y n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( y 0 cos ⁡ θ + x 0 sin ⁡ θ ) ( 其中  i 从  0 至  n − 1 ) \begin{align*} x_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(x_0\cos\theta - y_0\sin\theta) \quad (\text{其中 }i \text{ 从 }0 \text{ 至 }n - 1)\\ y_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(y_0\cos\theta + x_0\sin\theta) \quad (\text{其中 }i \text{ 从 }0 \text{ 至 }n - 1) \end{align*} xn​yn​​=∏i=0n−1​cosθi​1​(x0​cosθ−y0​sinθ)(其中 i 从 0 至 n−1)=∏i=0n−1​cosθi​1​(y0​cosθ+x0​sinθ)(其中 i 从 0 至 n−1)​

此时，已知条件有三个 x 0 x_0 x0​、 y 0 y_0 y0​ 和 θ \theta θ。通过 16 16 16 次迭代，我们可以得到 x n x_n xn​ 和 y n y_n yn​。而式中的 ∏ i = 0 n − 1 cos ⁡ θ i \prod_{i = 0}^{n - 1}\cos\theta_i ∏i=0n−1​cosθi​ 是个随 i i i 变化的值，我们可以预先将其值存入系统中。

然后，我们人为设置 x 0 = ∏ i = 0 n − 1 cos ⁡ θ i x_0 = \prod_{i = 0}^{n - 1}\cos\theta_i x0​=∏i=0n−1​cosθi​， y 0 = 0 y_0 = 0 y0​=0，则根据等式， x n = cos ⁡ θ x_n = \cos\theta xn​=cosθ， y n = sin ⁡ θ y_n = \sin\theta yn​=sinθ。其中 1 ∏ i = 0 n − 1 cos ⁡ θ i \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i} ∏i=0n−1​cosθi​1​ 的值我们也同样预先存入系统中。如此，我们就实现了正弦和余弦操作了。

二、CORDIC 的具体操作流程介绍

1、CORDIC 的旋转模式

由于算法较复杂，一休哥再总结一些具体的操作流程。

1、 设置迭代次数为 16 16 16，则 x 0 = 0.607253 x_0 = 0.607253 x0​=0.607253， y 0 = 0 y_0 = 0 y0​=0，并输入待计算的角度 θ \theta θ， θ \theta θ 在 [ − 99. 7 ∘ , 99. 7 ∘ ] [-99.7^{\circ}, 99.7^{\circ}] [−99.7∘,99.7∘] 范围内。

2、 根据三个迭代公式进行迭代， i i i 从 0 0 0 至 15 15 15：

x i + 1 = x i − d i y i 2 − i y i + 1 = y i + d i x i 2 − i z i + 1 = z i − d i θ i \begin{align*} x_{i + 1} &= x_i - d_iy_i2^{-i}\\ y_{i + 1} &= y_i + d_ix_i2^{-i}\\ z_{i + 1} &= z_i - d_i\theta_i \end{align*} xi+1​yi+1​zi+1​​=xi​−di​yi​2−i=yi​+di​xi​2−i=zi​−di​θi​​

注： z 0 = θ z_0 = \theta z0​=θ， d i d_i di​ 与 z i z_i zi​ 同符号。

3、 经过 16 16 16 次迭代计算后，得到的 x 16 x_{16} x16​ 和 y 16 y_{16} y16​ 分别为 cos ⁡ θ \cos\theta cosθ 和 sin ⁡ θ \sin\theta sinθ。

至此，关于 CORDIC 的三角函数 cos ⁡ θ \cos\theta cosθ 和 sin ⁡ θ \sin\theta sinθ 的计算原理讲解结束。

关于 CORDIC 算法计算三角函数 cos ⁡ θ \cos\theta cosθ 和 sin ⁡ θ \sin\theta sinθ 的 MATLAB 代码 如下所示：

close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 0.607253;%初始设置
z(1) = pi/4;%待求角度θ
%迭代操作
for i = 1:dieif z(i) >= 0d = 1;elsed = -1;endx(i+1) = x(i) - d*y(i)*(2^(-(i-1)));y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
cosa = vpa(x(17),10)
sina = vpa(y(17),10)
c = vpa(z(17),10)

2、CORDIC的向量模式

讲完了旋转模式后，我们接着讲讲向量模式下的圆坐标系。

在这里，我们需从头来过了，假设在 x y xy xy 坐标系中有一个点 P 0 ( x 0 , y 0 ) P0(x_0,y_0) P0(x0​,y0​) ，将 P 0 P0 P0 点绕原点旋转 θ \theta θ 角后得到点 P n ( x n , 0 ) Pn(x_n,0) Pn(xn​,0) ， θ \theta θ 在 [ − 99. 7 ∘ , 99. 7 ∘ ] [-99.7^{\circ},99.7^{\circ}] [−99.7∘,99.7∘] 范围内。

于是可以得到 P 0 P0 P0 和 P n Pn Pn 的关系：

x n = x 0 cos ⁡ θ − y 0 sin ⁡ θ = cos ⁡ θ ( x 0 − y 0 tan ⁡ θ ) y n = y 0 cos ⁡ θ + x 0 sin ⁡ θ = cos ⁡ θ ( y 0 + x 0 tan ⁡ θ ) = 0 \begin{align*} x_n &= x_0\cos\theta - y_0\sin\theta = \cos\theta(x_0 - y_0\tan\theta)\\ y_n &= y_0\cos\theta + x_0\sin\theta = \cos\theta(y_0 + x_0\tan\theta) = 0 \end{align*} xn​yn​​=x0​cosθ−y0​sinθ=cosθ(x0​−y0​tanθ)=y0​cosθ+x0​sinθ=cosθ(y0​+x0​tanθ)=0​

如何得到 P n ( x n , y n ) Pn(x_n,y_n) Pn(xn​,yn​) 一直是我们的目标。而此时，我们还是列出那几个等式：

根据三个迭代公式进行迭代， i i i 从 0 0 0 至 15 15 15 ：

x i + 1 = x i − d i y i 2 − i y i + 1 = y i + d i x i 2 − i z i + 1 = z i − d i θ i \begin{align*} x_{i + 1} &= x_i - d_iy_i2^{-i}\\ y_{i + 1} &= y_i + d_ix_i2^{-i}\\ z_{i + 1} &= z_i - d_i\theta_i \end{align*} xi+1​yi+1​zi+1​​=xi​−di​yi​2−i=yi​+di​xi​2−i=zi​−di​θi​​

不过此时我们尝试改变初始条件：

设置迭代次数为 16 16 16 ，则 x 0 = x x_0 = x x0​=x ， y 0 = y y_0 = y y0​=y ， z 0 = 0 z_0 = 0 z0​=0 ， d i d_i di​ 与 y i y_i yi​ 的符号相反。表示，经过 n n n 次旋转，使 P n Pn Pn 靠近 x x x 轴。

因此，当迭代结束之后， P n Pn Pn 将近似接近 x x x 轴，此时 y n = 0 y_n = 0 yn​=0 ，可知旋转了 θ \theta θ ，即 z n = θ = arctan ⁡ ( y / x ) z_n = \theta = \arctan(y/x) zn​=θ=arctan(y/x) 。

而

x n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( x 0 cos ⁡ θ − y 0 sin ⁡ θ ) ( 其中  i 从  0 至  n − 1 ) y n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( y 0 cos ⁡ θ + x 0 sin ⁡ θ ) ( 其中  i 从  0 至  n − 1 ) \begin{align*} x_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(x_0\cos\theta - y_0\sin\theta) \quad (\text{其中 }i \text{ 从 }0 \text{ 至 }n - 1)\\ y_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(y_0\cos\theta + x_0\sin\theta) \quad (\text{其中 }i \text{ 从 }0 \text{ 至 }n - 1) \end{align*} xn​yn​​=∏i=0n−1​cosθi​1​(x0​cosθ−y0​sinθ)(其中 i 从 0 至 n−1)=∏i=0n−1​cosθi​1​(y0​cosθ+x0​sinθ)(其中 i 从 0 至 n−1)​

因此，可得 y cos ⁡ θ + x sin ⁡ θ = 0 y\cos\theta + x\sin\theta = 0 ycosθ+xsinθ=0 ，

x n = 1 ∏ i = 0 n − 1 cos ⁡ θ i ( x cos ⁡ θ − y sin ⁡ θ ) = 1 ∏ i = 0 n − 1 cos ⁡ θ i { [ ( x cos ⁡ θ − y sin ⁡ θ ) 2 ] 1 2 } = 1 ∏ i = 0 n − 1 cos ⁡ θ i { [ x 2 cos ⁡ 2 θ + y 2 sin ⁡ 2 θ − 2 x y sin ⁡ θ cos ⁡ θ ] 1 2 } = 1 ∏ i = 0 n − 1 cos ⁡ θ i { [ x 2 cos ⁡ 2 θ + y 2 sin ⁡ 2 θ + y 2 cos ⁡ 2 θ + x 2 sin ⁡ 2 θ ] 1 2 } = 1 ∏ i = 0 n − 1 cos ⁡ θ i { [ x 2 + y 2 ] 1 2 } \begin{align*} x_n &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}(x\cos\theta - y\sin\theta)\\ &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}\{ [ (x\cos\theta - y\sin\theta)^2]^{\frac{1}{2}}\}\\ &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}\{ [ x^2\cos^2\theta + y^2\sin^2\theta - 2xy\sin\theta\cos\theta]^{\frac{1}{2}}\}\\ &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}\{ [ x^2\cos^2\theta + y^2\sin^2\theta + y^2\cos^2\theta + x^2\sin^2\theta]^{\frac{1}{2}}\}\\ &= \frac{1}{\prod_{i = 0}^{n - 1}\cos\theta_i}\{ [ x^2 + y^2]^{\frac{1}{2}}\} \end{align*} xn​​=∏i=0n−1​cosθi​1​(xcosθ−ysinθ)=∏i=0n−1​cosθi​1​{[(xcosθ−ysinθ)2]21​}=∏i=0n−1​cosθi​1​{[x2cos2θ+y2sin2θ−2xysinθcosθ]21​}=∏i=0n−1​cosθi​1​{[x2cos2θ+y2sin2θ+y2cos2θ+x2sin2θ]21​}=∏i=0n−1​cosθi​1​{[x2+y2]21​}​

由上可以知道，我们通过迭代，就算出了反正切函数 z n = θ = arctan ⁡ ( y / x ) z_n = \theta = \arctan(y/x) zn​=θ=arctan(y/x) ，以及向量 O P 0 → ( x , y ) \overrightarrow{OP_0}(x,y) OP0​ ​(x,y) 的长度 d = x n ⋅ ∏ i = 0 n − 1 cos ⁡ θ i d = x_n \cdot \prod_{i = 0}^{n - 1}\cos\theta_i d=xn​⋅∏i=0n−1​cosθi​ 。

关于反正切函数，一休哥要多啰嗦几句了，由于 θ \theta θ 在 [ − 99. 7 ∘ , 99. 7 ∘ ] [-99.7^{\circ},99.7^{\circ}] [−99.7∘,99.7∘] 范围内，所以我们输入向量 O P 0 → ( x , y ) \overrightarrow{OP_0}(x,y) OP0​ ​(x,y) 时，需要保证其在第一、四象限。

关于 CORDIC 算法计算反三角函数 arctan ⁡ θ \arctan\theta arctanθ 的 MATLAB 代码如下所示：

close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 100;%初始设置
y(1) = 200;%初始设置
k = 0.607253;%初始设置
%迭代操作
for i = 1:dieif y(i) >= 0d = -1;elsed = 1;endx(i+1) = x(i) - d*y(i)*(2^(-(i-1)));y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
d = vpa(x(17)*k,10)
a = vpa(y(17),10)
c = vpa(rad2deg(z(17)),10)

三、CORDIC 的旋转模式——Verilog 仿真

一休哥在编写CORDIC算法时，采用了 16 级流水线，仿真效果十分明显。以下是顶层文件的代码。

为了避免浮点运算，为了满足精度要求，一休哥对每个变量都放大了 2 16 2^{16} 216 倍，并且引入了有符号型 reg \text{reg} reg 和算术右移。

关于 Verilog 代码的编写，一休哥已经不想多说了，因为代码是完全符合我之前所讲的 CORDIC 的原理与 MATLAB 仿真代码。相信大家在看完本文的前两个部分之后，对 Verilog 的理解应该不是难事儿。

module Cordic_Test
(CLK_50M,RST_N,Phase,Sin,Cos,Error
);input                       CLK_50M;
input                       RST_N;
input       [31:0]          Phase;
output      [31:0]          Sin;
output      [31:0]          Cos;
output      [31:0]          Error;`define rot0  32'd2949120       //45度*2^16
`define rot1  32'd1740992       //26.5651度*2^16
`define rot2  32'd919872        //14.0362度*2^16
`define rot3  32'd466944        //7.1250度*2^16
`define rot4  32'd234368        //3.5763度*2^16
`define rot5  32'd117312        //1.7899度*2^16
`define rot6  32'd58688         //0.8952度*2^16
`define rot7  32'd29312         //0.4476度*2^16
`define rot8  32'd14656         //0.2238度*2^16
`define rot9  32'd7360          //0.1119度*2^16
`define rot10 32'd3648          //0.0560度*2^16
`define rot11 32'd1856          //0.0280度*2^16
`define rot12 32'd896           //0.0140度*2^16
`define rot13 32'd448           //0.0070度*2^16
`define rot14 32'd256           //0.0035度*2^16
`define rot15 32'd128           //0.0018度*2^16parameter Pipeline = 16;
parameter K = 32'h09b74;    //K=0.607253*2^16,32'h09b74,reg signed  [31:0]      Sin;
reg signed  [31:0]      Cos;
reg signed  [31:0]      Error;
reg signed  [31:0]      x0=0,y0=0,z0=0;
reg signed  [31:0]      x1=0,y1=0,z1=0;
reg signed  [31:0]      x2=0,y2=0,z2=0;
reg signed  [31:0]      x3=0,y3=0,z3=0;
reg signed  [31:0]      x4=0,y4=0,z4=0;
reg signed  [31:0]      x5=0,y5=0,z5=0;
reg signed  [31:0]      x6=0,y6=0,z6=0;
reg signed  [31:0]      x7=0,y7=0,z7=0;
reg signed  [31:0]      x8=0,y8=0,z8=0;
reg signed  [31:0]      x9=0,y9=0,z9=0;
reg signed  [31:0]      x10=0,y10=0,z10=0;
reg signed  [31:0]      x11=0,y11=0,z11=0;
reg signed  [31:0]      x12=0,y12=0,z12=0;
reg signed  [31:0]      x13=0,y13=0,z13=0;
reg signed  [31:0]      x14=0,y14=0,z14=0;
reg signed  [31:0]      x15=0,y15=0,z15=0;
reg signed  [31:0]      x16=0,y16=0,z16=0;
reg         [ 1:0]      Quadrant [Pipeline:0];always @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx0 <= 1'b0;                         y0 <= 1'b0;z0 <= 1'b0;endelsebeginx0 <= K;y0 <= 32'd0;z0 <= Phase[15:0] << 16;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx1 <= 1'b0;                         y1 <= 1'b0;z1 <= 1'b0;endelse if(z0[31])beginx1 <= x0 + y0;y1 <= y0 - x0;z1 <= z0 + `rot0;endelsebeginx1 <= x0 - y0;y1 <= y0 + x0;z1 <= z0 - `rot0;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx2 <= 1'b0;                         y2 <= 1'b0;z2 <= 1'b0;endelse if(z1[31])beginx2 <= x1 + (y1 >>> 1);y2 <= y1 - (x1 >>> 1);z2 <= z1 + `rot1;endelsebeginx2 <= x1 - (y1 >>> 1);y2 <= y1 + (x1 >>> 1);z2 <= z1 - `rot1;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx3 <= 1'b0;                         y3 <= 1'b0;z3 <= 1'b0;endelse if(z2[31])beginx3 <= x2 + (y2 >>> 2);y3 <= y2 - (x2 >>> 2);z3 <= z2 + `rot2;endelsebeginx3 <= x2 - (y2 >>> 2);y3 <= y2 + (x2 >>> 2);z3 <= z2 - `rot2;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx4 <= 1'b0;                         y4 <= 1'b0;z4 <= 1'b0;endelse if(z3[31])beginx4 <= x3 + (y3 >>> 3);y4 <= y3 - (x3 >>> 3);z4 <= z3 + `rot3;endelsebeginx4 <= x3 - (y3 >>> 3);y4 <= y3 + (x3 >>> 3);z4 <= z3 - `rot3;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx5 <= 1'b0;                         y5 <= 1'b0;z5 <= 1'b0;endelse if(z4[31])beginx5 <= x4 + (y4 >>> 4);y5 <= y4 - (x4 >>> 4);z5 <= z4 + `rot4;endelsebeginx5 <= x4 - (y4 >>> 4);y5 <= y4 + (x4 >>> 4);z5 <= z4 - `rot4;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx6 <= 1'b0;                         y6 <= 1'b0;z6 <= 1'b0;endelse if(z5[31])beginx6 <= x5 + (y5 >>> 5);y6 <= y5 - (x5 >>> 5);z6 <= z5 + `rot5;endelsebeginx6 <= x5 - (y5 >>> 5);y6 <= y5 + (x5 >>> 5);z6 <= z5 - `rot5;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx7 <= 1'b0;                         y7 <= 1'b0;z7 <= 1'b0;endelse if(z6[31])beginx7 <= x6 + (y6 >>> 6);y7 <= y6 - (x6 >>> 6);z7 <= z6 + `rot6;endelsebeginx7 <= x6 - (y6 >>> 6);y7 <= y6 + (x6 >>> 6);z7 <= z6 - `rot6;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx8 <= 1'b0;                         y8 <= 1'b0;z8 <= 1'b0;endelse if(z7[31])beginx8 <= x7 + (y7 >>> 7);y8 <= y7 - (x7 >>> 7);z8 <= z7 + `rot7;endelsebeginx8 <= x7 - (y7 >>> 7);y8 <= y7 + (x7 >>> 7);z8 <= z7 - `rot7;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx9 <= 1'b0;                         y9 <= 1'b0;z9 <= 1'b0;endelse if(z8[31])beginx9 <= x8 + (y8 >>> 8);y9 <= y8 - (x8 >>> 8);z9 <= z8 + `rot8;endelsebeginx9 <= x8 - (y8 >>> 8);y9 <= y8 + (x8 >>> 8);z9 <= z8 - `rot8;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx10 <= 1'b0;                        y10 <= 1'b0;z10 <= 1'b0;endelse if(z9[31])beginx10 <= x9 + (y9 >>> 9);y10 <= y9 - (x9 >>> 9);z10 <= z9 + `rot9;endelsebeginx10 <= x9 - (y9 >>> 9);y10 <= y9 + (x9 >>> 9);z10 <= z9 - `rot9;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx11 <= 1'b0;                        y11 <= 1'b0;z11 <= 1'b0;endelse if(z10[31])beginx11 <= x10 + (y10 >>> 10);y11 <= y10 - (x10 >>> 10);z11 <= z10 + `rot10;endelsebeginx11 <= x10 - (y10 >>> 10);y11 <= y10 + (x10 >>> 10);z11 <= z10 - `rot10;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx12 <= 1'b0;                        y12 <= 1'b0;z12 <= 1'b0;endelse if(z11[31])beginx12 <= x11 + (y11 >>> 11);y12 <= y11 - (x11 >>> 11);z12 <= z11 + `rot11;endelsebeginx12 <= x11 - (y11 >>> 11);y12 <= y11 + (x11 >>> 11);z12 <= z11 - `rot11;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx13 <= 1'b0;                        y13 <= 1'b0;z13 <= 1'b0;endelse if(z12[31])beginx13 <= x12 + (y12 >>> 12);y13 <= y12 - (x12 >>> 12);z13 <= z12 + `rot12;endelsebeginx13 <= x12 - (y12 >>> 12);y13 <= y12 + (x12 >>> 12);z13 <= z12 - `rot12;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx14 <= 1'b0;                        y14 <= 1'b0;z14 <= 1'b0;endelse if(z13[31])beginx14 <= x13 + (y13 >>> 13);y14 <= y13 - (x13 >>> 13);z14 <= z13 + `rot13;endelsebeginx14 <= x13 - (y13 >>> 13);y14 <= y13 + (x13 >>> 13);z14 <= z13 - `rot13;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx15 <= 1'b0;                        y15 <= 1'b0;z15 <= 1'b0;endelse if(z14[31])beginx15 <= x14 + (y14 >>> 14);y15 <= y14 - (x14 >>> 14);z15 <= z14 + `rot14;endelsebeginx15 <= x14 - (y14 >>> 14);y15 <= y14 + (x14 >>> 14);z15 <= z14 - `rot14;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginx16 <= 1'b0;                        y16 <= 1'b0;z16 <= 1'b0;endelse if(z15[31])beginx16 <= x15 + (y15 >>> 15);y16 <= y15 - (x15 >>> 15);z16 <= z15 + `rot15;endelsebeginx16 <= x15 - (y15 >>> 15);y16 <= y15 + (x15 >>> 15);z16 <= z15 - `rot15;end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginQuadrant[0] <= 1'b0;Quadrant[1] <= 1'b0;Quadrant[2] <= 1'b0;Quadrant[3] <= 1'b0;Quadrant[4] <= 1'b0;Quadrant[5] <= 1'b0;Quadrant[6] <= 1'b0;Quadrant[7] <= 1'b0;Quadrant[8] <= 1'b0;Quadrant[9] <= 1'b0;Quadrant[10] <= 1'b0;Quadrant[11] <= 1'b0;Quadrant[12] <= 1'b0;Quadrant[13] <= 1'b0;Quadrant[14] <= 1'b0;Quadrant[15] <= 1'b0;Quadrant[16] <= 1'b0;endelsebeginQuadrant[0] <= Phase[17:16];Quadrant[1] <= Quadrant[0];Quadrant[2] <= Quadrant[1];Quadrant[3] <= Quadrant[2];Quadrant[4] <= Quadrant[3];Quadrant[5] <= Quadrant[4];Quadrant[6] <= Quadrant[5];Quadrant[7] <= Quadrant[6];Quadrant[8] <= Quadrant[7];Quadrant[9] <= Quadrant[8];Quadrant[10] <= Quadrant[9];Quadrant[11] <= Quadrant[10];Quadrant[12] <= Quadrant[11];Quadrant[13] <= Quadrant[12];Quadrant[14] <= Quadrant[13];Quadrant[15] <= Quadrant[14];Quadrant[16] <= Quadrant[15];end
endalways @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)beginCos <= 1'b0;Sin <= 1'b0;Error <= 1'b0;endelsebeginError <= z16;case(Quadrant[16])2'b00: //if the Phase is in first Quadrant,the Sin(X)=Sin(A),Cos(X)=Cos(A)beginCos <= x16;Sin <= y16;end2'b01: //if the Phase is in second Quadrant,the Sin(X)=Sin(A+90)=CosA,Cos(X)=Cos(A+90)=-SinAbeginCos <= ~(y16) + 1'b1;//-SinSin <= x16;//Cosend2'b10: //if the Phase is in third Quadrant,the Sin(X)=Sin(A+180)=-SinA,Cos(X)=Cos(A+180)=-CosAbeginCos <= ~(x16) + 1'b1;//-CosSin <= ~(y16) + 1'b1;//-Sinend2'b11: //if the Phase is in forth Quadrant,the Sin(X)=Sin(A+270)=-CosA,Cos(X)=Cos(A+270)=SinAbeginCos <= y16;//SinSin <= ~(x16) + 1'b1;//-Cosendendcaseend
endendmodule

以下是testbench文件代码

`timescale 1 ps/ 1 psmodule Cordic_Test_tb;// Inputs
reg                         CLK_50M;
reg                         RST_N;
reg             [15:0]      cnt;
reg             [15:0]      cnt_n;
reg             [31:0]      Phase;
reg             [31:0]      Phase_n;
wire            [31:0]      Sin;
wire            [31:0]      Cos;
wire            [31:0]      Error;// Instantiate the Unit Under Test (UUT)
Cordic_Test                 uut 
(.CLK_50M                (CLK_50M    ),.RST_N                  (RST_N      ),.Phase                  (Phase      ),.Sin                    (Sin        ),.Cos                    (Cos        ),.Error                  (Error      )
);initial
begin#0 CLK_50M = 1'b0;#10000 RST_N = 1'b0;#10000 RST_N = 1'b1;#10000000 $stop;
end 
always #10000 
beginCLK_50M = ~CLK_50M;
end
always @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)cnt <= 1'b0;elsecnt <= cnt_n;
endalways @ (*)
beginif(cnt == 16'd359)cnt_n = 1'b0;elsecnt_n = cnt + 1'b1;
end
//生成相位0-359度,Phase[17:16]为相位的象限,Phase[15:10]为相位的值
always @ (posedge CLK_50M or negedge RST_N)
beginif(!RST_N)Phase <= 1'b0;elsePhase <= Phase_n;
endalways @ (*)
beginif(cnt <= 16'd90)Phase_n = cnt;else if(cnt > 16'd90 && cnt <= 16'd180)Phase_n = {2'd01,cnt - 16'd90};else if(cnt > 16'd180 && cnt <= 16'd270)Phase_n = {2'd10,cnt - 16'd180};else if(cnt > 16'd270)Phase_n = {2'd11,cnt - 16'd270};
endendmodule

最后来一张效果图，可以发现，我们的 16 级流水线已经正常的运行起来了，由于我们仿真输入的相位值为 0-359 度循环，因此 sin 和 cos 也循环了～～～

这里写图片描述

CORDIC 算法详解及 FPGA 实现

ngany 于 2021-05-30 18:52:04 发布

CORDIC 算法详解

1 平面坐标系旋转

CORDIC 算法的思想是通过迭代的方法，使得累计旋转过的角度的和无限接近目标角度。它是一种数值计算逼近的方法，运算只有移位和加减。

通过圆坐标系可以了解 CORDIC 算法的基本思想，如图 1 所示，初始向量 ( x 1 , y 1 ) \left (x_{1},y_{1} \right) (x1​,y1​)旋转 θ \theta θ角度之后得到向量 ( x 2 , y 2 ) \left ( x_{2},y_{2} \right) (x2​,y2​)，两者之间满足（公式 1）关系。

img

图 1 CORDIC 算法原理示意图
$$\left{ x2=x1cosθn−y1sinθny2=y1cosθn−x1sinθn\begin {matrix} x_{2} = x_{1} \cos\theta_{n} - y_{1} \sin\theta_{n} \ y_{2} = y_{1} \cos\theta_{n} - x_{1}\sin\theta_{n} \ \end {matrix} \right.$$

通过提取因数 cos ⁡ θ \cos\theta cosθ，方程式可以改写成下面的形式：

x 2 = x 1 cos ⁡ θ − y 1 sin ⁡ θ = cos ⁡ θ ( x 1 − y 1 tan ⁡ θ ) y 2 = y 1 cos ⁡ θ + x 1 sin ⁡ θ = cos ⁡ θ ( y 1 + x 1 tan ⁡ θ ) \begin{align*} x_{2} &= x_{1} \cos\theta - y_{1} \sin\theta = \cos\theta(x_{1} - y_{1}\tan\theta) \\ y_{2} &= y_{1} \cos\theta + x_{1} \sin\theta = \cos\theta(y_{1} + x_{1}\tan\theta) \end{align*} x2​y2​​=x1​cosθ−y1​sinθ=cosθ(x1​−y1​tanθ)=y1​cosθ+x1​sinθ=cosθ(y1​+x1​tanθ)​

2 伪旋转

如果去掉 cos ⁡ θ \cos\theta cosθ，我们可以的到伪旋转方程式（公式 3），即旋转的角度是正确的，但是 x x x， y y y 的值增加了 cos ⁡ − 1 θ \cos^{- 1}\theta cos−1θ 倍，由于 cos ⁡ − 1 θ > 1 \cos^{- 1}\theta > 1 cos−1θ>1，所以模值变大。这里并不能通过数学方法去除 cos ⁡ θ \cos\theta cosθ项，但是可以化简坐标平面旋转的计算。

x ^ 2 = x 1 − y 1 tan ⁡ θ y ^ 2 = y 1 + x 1 tan ⁡ θ \begin{align*} \widehat{x}_{2} &= x_{1} - y_{1}\tan\theta \\ \widehat{y}_{2} &= y_{1} + x_{1}\tan\theta \end{align*} x 2​y ​2​​=x1​−y1​tanθ=y1​+x1​tanθ​

img

图 2 去除 cos ⁡ θ \cos\theta cosθ后伪坐标系

3 CORDIC 方法

这里为了便于硬件的计算，采用迭代的思想，旋转角度 θ \theta θ 可以通过若干步实现，每一步旋转一个角度 θ i \theta^{i} θi 。并且约定每一次旋转的角度的正切值为 2 的倍数，即 tan ⁡ θ i = 2 − i {\tan\theta^{i} = 2}^{- i} tanθi=2−i 。下面表格是用于 CORDIC 算法中每个迭代 i i i 的旋转角度。这样，乘以正切值就可以变成移位操作。

表 1 迭代角度 θ i \theta^{i} θi正切值

i i i θ i \theta^{i} θi（degree） tan ⁡ θ i = 2 − i {\tan\theta^{i} = 2}^{- i} tanθi=2−i
045.01
126.5550511770.5
214.0362434670.25
37.1250163480.125
43.5763343740.0625

4 角度累加器

引入控制算子 d i d_{i} di​，用于确定旋转的方向。其中第 i i i 步顺时针旋转时 d i = − 1 d_{i} = - 1 di​=−1，逆时针旋转 d i = 1 d_{i} = 1 di​=1。前面的伪旋转坐标方程现在可以表示为：

x i + 1 = x i − d i 2 − i y i y i + 1 = y i + d i 2 − i x i \begin{align*} x_{i + 1} &= x_{i} - d_{i}2^{- i}y_{i} \\ y_{i + 1} &= y_{i} + d_{i}2^{- i}x_{i} \end{align*} xi+1​yi+1​​=xi​−di​2−iyi​=yi​+di​2−ixi​​

这里，我们引入第三个方程，被称为角度累加器，用来在每次迭代过程中追踪累加的旋转角度，表示第 n n n 次旋转后剩下未旋转的角度，定义为

z i + 1 = z i − d i θ i z_{i + 1} = z_{i} - d_{i} \theta^{i} zi+1​=zi​−di​θi，其中 d i = ± 1 d_{i} = \pm 1 di​=±1

5 移位 - 加法算法

因此，原始的算法现在已经被简化为使用向量的伪旋转方程式（公式 6）来表示迭代（移位 - 加法）算法。

  • 2 次移位；
    （ 2 − i 2^{- i} 2−i用移位实现，每右移 n 位就把原来数值乘以 2 的 - i 次方了）

  • 1 次查找表；（每一次迭代都会有一个固定角度 θ i \theta^{i} θi的累加，这个角度是 2 − i 2^{- i} 2−i对应的角度值，使用查表实现。 θ i = arc tan ⁡ 2 − i \theta^{i} = {\text {arc}\tan} 2^{- i} θi=arctan2−i）

  • 3 次加法；（x，y，z 的累加，共三次）

x i + 1 = x i − d i 2 − i y i y i + 1 = y i + d i 2 − i x i z i + 1 = z i − d i θ i \begin{align*} x_{i + 1} &= x_{i} - d_{i}2^{- i}y_{i} \\ y_{i + 1} &= y_{i} + d_{i}2^{- i}x_{i} \\ z_{i + 1} &= z_{i} - d_{i}\theta_{i} \end{align*} xi+1​yi+1​zi+1​​=xi​−di​2−iyi​=yi​+di​2−ixi​=zi​−di​θi​​

6 伸缩因子

当简化算法以伪旋转时， cos ⁡ θ \cos\theta cosθ项被忽略，这样 ( x n , y n ) \left ( x_{n},y_{n} \right) (xn​,yn​) 就被伸缩了 K n K_{n} Kn​ 倍。如果迭代次数已知，可以预先计算伸缩因子 K n K_{n} Kn​。同样 1 / K n 1/K_{n} 1/Kn​也可被预先计算以得到 ( x n , y n ) \left ( x_{n},y_{n} \right) (xn​,yn​) 的真值。

K n = ∏ n 1 cos ⁡ θ i = ∏ n ( 1 + 2 − 2 i ) K_{n} = \prod_{n}^{}\frac {1}{\cos\theta^{i}} = \prod_{n}^{}\left ( \sqrt {1 + 2^{- 2i}} \right) Kn​=∏n​cosθi1​=∏n​(1+2−2i ​)

这里 K n − > 1.64676 K_{n} - > 1.64676 Kn​−>1.64676，当 n − > ∞ n - > \infty n−>∞

1 / K n − > 0.607253 1/K_{n} - > 0.607253 1/Kn​−>0.607253，当 n − > ∞ n - > \infty n−>∞

7 旋转模式

CORDIC 方法有两种模式，旋转模式和向量模式。工作模式决定了控制算子 d i d_{i} di​ 的条件。在旋转模式中，旋转剩余角度初始变量 z 0 = θ z_{0} = \theta z0​=θ，经过 n 次旋转后，使 z 0 = 0 z_{0} = 0 z0​=0。整个旋转过程可以表示为一系列旋转角度不断偏摆，从而逼近所需旋转角度的迭代过程。n 次迭代后可以得到：

x n = K n ( x 0 cos ⁡ z 0 − y 0 sin ⁡ z 0 ) y n = K n ( y 0 cos ⁡ z 0 + x 0 sin ⁡ z 0 ) z n = 0 \begin{align*} x_{n} &= K_{n}(x_{0} \cos z_{0} - y_{0} \sin z_{0}) \\ y_{n} &= K_{n}(y_{0} \cos z_{0} + x_{0} \sin z_{0}) \\ z_{n} &= 0 \end{align*} xn​yn​zn​​=Kn​(x0​cosz0​−y0​sinz0​)=Kn​(y0​cosz0​+x0​sinz0​)=0​

通过设置 x 0 = 1 / K n = 0.6073 x_{0} = 1/K_{n} = 0.6073 x0​=1/Kn​=0.6073 和 y 0 = 0 y_{0} = 0 y0​=0 可以计算 cos ⁡ z 0 \cos z_{0} cosz0​和 sin ⁡ z 0 \sin z_{0} sinz0​。分析可知 CORDIC 算法在圆周系统旋转模式下可以用来计算一个输入角的正弦值、余弦值。

x n = K n ( x 0 cos ⁡ z 0 − y 0 sin ⁡ z 0 ) = cos ⁡ θ y n = K n ( y 0 cos ⁡ z 0 + x 0 sin ⁡ z 0 ) = sin ⁡ θ \begin{align*} x_{n} &= K_{n}(x_{0} \cos z_{0} - y_{0} \sin z_{0}) = \cos\theta \\ y_{n} &= K_{n}(y_{0} \cos z_{0} + x_{0} \sin z_{0}) = \sin\theta \end{align*} xn​yn​​=Kn​(x0​cosz0​−y0​sinz0​)=cosθ=Kn​(y0​cosz0​+x0​sinz0​)=sinθ​

img

图 3 旋转模式角度逼近

8 象限判断

对于任意角度 θ \theta θ，都可以通过旋转一系列小角度来 i i i 完成。第一次迭代旋转 4 5 ∘ 45^{\circ} 45∘，第二次迭代旋转 26. 6 ∘ 26.6^{\circ} 26.6∘，第三次迭代旋转 1 4 ∘ 14^{\circ} 14∘。很显然，每次旋转的方向都影响到最终的累计角度。在 − 99. 7 ∘ < θ < 99. 7 ∘ - 99.7^{\circ}< \theta < 99.7^{\circ} −99.7∘<θ<99.7∘ 的范围内任意角度都可以旋转。对于该角度范围之外的角度，可以通过三角函数等式转化成该范围内的角度。因此设计时通常把角度 θ \theta θ 转化到第一象限角，根据 θ \theta θ 所在的圆坐标系象限获得 x n x_{n} xn​ 和 y n y_{n} yn​。

9 溢出处理

通过表 2 可以看出，把初始 θ \theta θ 角度设置为 90°，由于 x 0 x_{0} x0​ 赋的初值存在误差（一般是偏大），最终获得的 x n x_{n} xn​ 和 y n y_{n} yn​ 是有可能大于 1 的。所以设计时需要做溢出保护。或者把 x 0 x_{0} x0​ 初值减小，这可能会牺牲精度。

表 2 θ \theta θ 接近 90° 数据溢出

idthetazyxSINCOS
014589.997000.6073019900
1126.644.99700.60730.60731990019900
211418.39700.91100.3037298509950
317.14.39700.98690.0759323382488
4-13.6-2.70300.9964-0.047432648-1555
511.80.89700.99930.014832746486
6-10.9-0.90300.9998-0.016432761-537
7-10.4-0.00301.0000-0.000832769-26
810.20.39701.00000.007032769230
910.10.19701.00010.003132770102
1010.0560.09701.00010.00123277038
1110.0270.04101.00010.0002327716

10 Verilog 代码实现

CORDIC 算法代码

module MyCORDIC (input clk,input rst_n,input  [15:0] theta,output reg [15:0] sin_theta,output reg [15:0] cos_theta
);parameter Kn  = 'd19898;    // 0.607253*2^15
parameter iKn = 'd53961;    // 1.64676*2^15 parameter arctan_0 = 8192    ;  //arctan (1/2)
parameter arctan_1 = 4836    ;  //arctan (1/2^1)
parameter arctan_2 = 2555    ;  //arctan (1/2^2)
parameter arctan_3 = 1297    ;  //arctan (1/2^3)
parameter arctan_4 = 651     ;  //arctan (1/2^4)
parameter arctan_5 = 326     ;  //arctan (1/2^5)
parameter arctan_6 = 163     ;  //arctan (1/2^6)
parameter arctan_7 = 81      ;  //arctan (1/2^7)
parameter arctan_8 = 41      ;  //arctan (1/2^8)
parameter arctan_9 = 20      ;  //arctan (1/2^9)
parameter arctan_10 = 10     ;  //arctan (1/2^10)
parameter arctan_11 = 5      ;  //arctan (1/2^11)reg signed [15:0] x [11:0];
reg signed [15:0] y [11:0];
reg signed [15:0] z [11:0];wire [15:0] x_tmp;
wire [15:0] y_tmp;reg signed [15:0] theta_1;
wire [2:0] Quadrant;//theta 角所在的象限// 象限判断
assign Quadrant = theta [15:14] + 1;always@(*)
beginbegintheta_1 <= {2'b00,theta [13:0]};if (Quadrant==1)begintheta_1 <= theta;endelse if (Quadrant==2)begintheta_1 <= 32768 - theta;endelse if (Quadrant==3)begintheta_1 <= theta - 32768;endelse if (Quadrant==4)begintheta_1 <= 65536 - theta;endend
endalways@(posedge clk or negedge rst_n)
beginif (!rst_n)beginx [0] <= 16'd0;y [0] <= 16'd0;z [0] <= 16'd0;endelsebeginx [0] <= Kn;y [0] <= 16'd0;z [0] <= theta_1;end
endalways@(posedge clk or negedge rst_n) //i=0
beginif (!rst_n)beginx [1] <= 16'd0;y [1] <= 16'd0;z [1] <= 16'd0;endelsebeginif (z [0][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [1] <= x [0] + y [0];y [1] <= y [0] - x [0];z [1] <= z [0] + arctan_0;end          // 剩余角度为正数，顺时针旋转，d=+1elsebeginx [1] <= x [0] - y [0];y [1] <= y [0] + x [0];z [1] <= z [0] - arctan_0;endend
end// >>> 符号表示算术右移，不改变符号位
always@(posedge clk or negedge rst_n) //i=1
beginif (!rst_n)beginx [2] <= 16'd0;y [2] <= 16'd0;z [2] <= 16'd0;endelsebeginif (z [1][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [2] <= x [1] + (y [1] >>> 1);y [2] <= y [1] - (x [1] >>> 1);z [2] <= z [1] + arctan_1;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [2] <= x [1] - (y [1] >>> 1);y [2] <= y [1] + (x [1] >>> 1);z [2] <= z [1] - arctan_1;endend
endalways@(posedge clk or negedge rst_n) //i=2
beginif (!rst_n)beginx [3] <= 16'd0;y [3] <= 16'd0;z [3] <= 16'd0;endelsebeginif (z [2][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [3] <= x [2] + (y [2] >>> 2);y [3] <= y [2] - (x [2] >>> 2);z [3] <= z [2] + arctan_2;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [3] <= x [2] - (y [2] >>> 2);y [3] <= y [2] + (x [2] >>> 2);z [3] <= z [2] - arctan_2;endend
endalways@(posedge clk or negedge rst_n) //i=3
beginif (!rst_n)beginx [4] <= 16'd0;y [4] <= 16'd0;z [4] <= 16'd0;endelsebeginif (z [3][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [4] <= x [3] + (y [3] >>> 3);y [4] <= y [3] - (x [3] >>> 3);z [4] <= z [3] + arctan_3;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [4] <= x [3] - (y [3] >>> 3);y [4] <= y [3] + (x [3] >>> 3);z [4] <= z [3] - arctan_3;endend
endalways@(posedge clk or negedge rst_n) //i=4
beginif (!rst_n)beginx [5] <= 16'd0;y [5] <= 16'd0;z [5] <= 16'd0;endelsebeginif (z [4][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [5] <= x [4] + (y [4] >>> 4);y [5] <= y [4] - (x [4] >>> 4);z [5] <= z [4] + arctan_4;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [5] <= x [4] - (y [4] >>> 4);y [5] <= y [4] + (x [4] >>> 4);z [5] <= z [4] - arctan_4;endend
endalways@(posedge clk or negedge rst_n) //i=5
beginif (!rst_n)beginx [6] <= 16'd0;y [6] <= 16'd0;z [6] <= 16'd0;endelsebeginif (z [5][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [6] <= x [5] + (y [5] >>> 5);y [6] <= y [5] - (x [5] >>> 5);z [6] <= z [5] + arctan_5;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [6] <= x [5] - (y [5] >>> 5);y [6] <= y [5] + (x [5] >>> 5);z [6] <= z [5] - arctan_5;endend
endalways@(posedge clk or negedge rst_n) //i=6
beginif (!rst_n)beginx [7] <= 16'd0;y [7] <= 16'd0;z [7] <= 16'd0;endelsebeginif (z [6][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [7] <= x [6] + (y [6] >>> 6);y [7] <= y [6] - (x [6] >>> 6);z [7] <= z [6] + arctan_6;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [7] <= x [6] - (y [6] >>> 6);y [7] <= y [6] + (x [6] >>> 6);z [7] <= z [6] - arctan_6;endend
endalways@(posedge clk or negedge rst_n) //i=7
beginif (!rst_n)beginx [8] <= 16'd0;y [8] <= 16'd0;z [8] <= 16'd0;endelsebeginif (z [7][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [8] <= x [7] + (y [7] >>> 7);y [8] <= y [7] - (x [7] >>> 7);z [8] <= z [7] + arctan_7;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [8] <= x [7] - (y [7] >>> 7);y [8] <= y [7] + (x [7] >>> 7);z [8] <= z [7] - arctan_7;endend
endalways@(posedge clk or negedge rst_n) //i=8
beginif (!rst_n)beginx [9] <= 16'd0;y [9] <= 16'd0;z [9] <= 16'd0;endelsebeginif (z [8][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [9] <= x [8] + (y [8] >>> 8);y [9] <= y [8] - (x [8] >>> 8);z [9] <= z [8] + arctan_8;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [9] <= x [8] - (y [8] >>> 8);y [9] <= y [8] + (x [8] >>> 8);z [9] <= z [8] - arctan_8;endend
endalways@(posedge clk or negedge rst_n) //i=9
beginif (!rst_n)beginx [10] <= 16'd0;y [10] <= 16'd0;z [10] <= 16'd0;endelsebeginif (z [9][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [10] <= x [9] + (y [9] >>> 9);y [10] <= y [9] - (x [9] >>> 9);z [10] <= z [9] + arctan_9;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [10] <= x [9] - (y [9] >>> 9);y [10] <= y [9] + (x [9] >>> 9);z [10] <= z [9] - arctan_9;endend
endalways@(posedge clk or negedge rst_n) //i=10
beginif (!rst_n)beginx [11] <= 16'd0;y [11] <= 16'd0;z [11] <= 16'd0;endelsebeginif (z [10][15]) // 剩余角度为负数，顺时针旋转，d=-1beginx [11] <= x [10] + (y [10] >>> 10);y [11] <= y [10] - (x [10] >>> 10);z [11] <= z [10] + arctan_10;end          // 剩余角度为正数，逆时针旋转，d=+1elsebeginx [11] <= x [10] - (y [10] >>> 10);y [11] <= y [10] + (x [10] >>> 10);z [11] <= z [10] - arctan_10;endend
end// 溢出判断
assign x_tmp = x [11][15]==1 ? 16'h7FFF : x [11];
assign y_tmp = y [11][15]==1 ? 16'h7FFF : y [11];
//assign x_tmp = x [11];
//assign y_tmp = y [11];always@(posedge clk or negedge rst_n) //i=11
beginif (!rst_n)beginsin_theta <= 16'd0;cos_theta <= 16'd0;endelsebeginif (Quadrant == 3'd1)beginsin_theta <= y_tmp;cos_theta <= x_tmp;endelse if (Quadrant == 3'd2)beginsin_theta <= y_tmp;cos_theta <= -x_tmp;endelse if (Quadrant == 3'd3)beginsin_theta <= -y_tmp;cos_theta <= -x_tmp;endelse if (Quadrant == 3'd4)beginsin_theta <= -y_tmp;cos_theta <= x_tmp;endelsebeginsin_theta <= sin_theta;cos_theta <= cos_theta;endend
end
endmodule

testbench 文件

`timescale 1 ns/ 1 nsmodule MyCORDIC_tb (
);integer i;reg clk,rst_n;
reg [15:0] theta,theta_n;
wire [15:0] sin_theta,cos_theta;reg [15:0] cnt,cnt_n;MyCORDIC u0 (.clk       (clk      ),.rst_n     (rst_n    ),.theta     (theta    ),.sin_theta (sin_theta),.cos_theta (cos_theta)
);initial
begin#0 clk = 1'b0;#10 rst_n = 1'b0;#10 rst_n = 1'b1;#10000000$stop;
end initial
begin#0 theta = 16'd20;for (i=0;i<10000;i=i+1)begin#400;theta <= theta + 16'd200;end
end always #10
beginclk = ~clk;
endendmodule

ModelSim 仿真

img

参考文献

  1. XILINX FPGAs for DSP CORDIC 算法 [OL].
  2. 张剑锋。基于改进 CORDIC 算法的 DDFS 和 FFT 研究与实现 [D].
    国防科学技术大学，2011.
  3. Cordic 算法的原理介绍 [OL].
    https://www.cnblogs.com/touchblue/p/3535968.html
  4. cordic 算法详解 [OL].
    https://blog.csdn.net/u010712012/article/details/77755567

via:

  • Cordic 算法的原理介绍 - 乐富道 - 博客园 乐富道 2014-01-28 23:05
    https://www.cnblogs.com/touchblue/p/3535968.html

  • 基于 FPGA 的 CORDIC 算法实现 ——Verilog 版_cordic 算法详解 一休哥 - CSDN 博客 善良的一休君于 2017-08-21 20:07:34 发布.
    https://blog.csdn.net/qq_39210023/article/details/77456031

  • CORDIC 算法原理详解及其 Verilog 实现_verilog cordic 算法 - CSDN 博客 爱吃蛋挞的Dolly
    于 2021-01-11 16:54:10 发布
    https://blog.csdn.net/gemengxia/article/details/112475073

  • CORDIC 算法详解及 FPGA 实现 - CSDN 博客 ngany 于 2021-05-30 18:52:04 发布
    https://blog.csdn.net/ngany/article/details/117401494

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/889828.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

前端(vue组件)

前端(vue组件)

1组件对象 1.1定义组件对象 defineComponent( {} ) 1.2注册组件 1.3使用组件 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-sca…
阅读更多...
MySQL八股-MVCC入门

MySQL八股-MVCC入门

文章目录 当前读&#xff08;加锁&#xff09;快照读&#xff08;不加锁&#xff09;MVCC隐藏字段undo-log版本链A. 第一步B.第二步C. 第三步 readview MVCC原理分析RCA. 先来看第一次快照读具体的读取过程&#xff1a;B. 再来看第二次快照读具体的读取过程: RR隔离级别 当前读…
阅读更多...
初始Python篇（6）—— 字符串

初始Python篇（6）—— 字符串

找往期文章包括但不限于本期文章中不懂的知识点&#xff1a; 个人主页&#xff1a;我要学编程(ಥ_ಥ)-CSDN博客 所属专栏&#xff1a; Python 目录 字符串的常见操作 格式化字符串 占位符 f-string 字符串的 format 方法 字符串的编码与解码 与数据验证相关的方法 …
阅读更多...
从 CephFS 到 JuiceFS：同程旅游亿级文件存储平台构建之路

从 CephFS 到 JuiceFS：同程旅游亿级文件存储平台构建之路

随着公司业务的快速发展&#xff0c;同程旅行的非结构化的数据突破 10 亿&#xff0c;在 2022 年&#xff0c;同程首先完成了对象存储服务的建设。当时&#xff0c;分布式文件系统方面&#xff0c;同程使用的是 CephFS&#xff0c;随着数据量的持续增长&#xff0c;CephFS 的高…
阅读更多...
Jenkins参数化构建详解(This project is parameterized)

Jenkins参数化构建详解(This project is parameterized)

本文详细介绍了Jenkins中不同类型的参数化构建方法&#xff0c;包括字符串、选项、多行文本、布尔值和git分支参数的配置&#xff0c;以及如何使用ActiveChoiceParameter实现动态获取参数选项。通过示例展示了传统方法和声明式pipeline的语法 文章目录 1. Jenkins的参数化构建1…
阅读更多...
【图像处理】利用numpy实现直方图均衡、自适应直方图均衡、对比度受限自适应直方图均衡

【图像处理】利用numpy实现直方图均衡、自适应直方图均衡、对比度受限自适应直方图均衡

直方图均衡化是一种在图像处理技术&#xff0c;通过调整图像的直方图来增强图像的对比度。 本博客不利用opencv库&#xff0c;仅利用numpy、matplotlib来实现直方图均衡、自适应直方图均衡、对比度受限自适应直方图均衡 直方图均衡 包括四个流程 计算图像RGB三通道的归一化直…
阅读更多...
组织空转数据（人类+小鼠）

组织空转数据（人类+小鼠）

空间转录组&#xff08;Spatial Transcriptomics&#xff09;是一种新兴的高通量基因组学技术&#xff0c;它允许我们在组织切片中同时获取基因表达信息和细胞的空间位置信息。其可以帮助我们更好地理解细胞在组织中的空间分布和相互作用&#xff0c;揭示组织发育、器官功能和疾…
阅读更多...
[数据结构#1] 并查集 | FindRoot | Union | 优化 | 应用

[数据结构#1] 并查集 | FindRoot | Union | 优化 | 应用

目录 1. 并查集原理 问题背景 名称与编号映射 数据结构设计 2. 并查集基本操作 (1) 初始化 (2) 查询根节点 (FindRoot) (3) 合并集合 (Union) (4) 集合操作总结 并查集优化 (1) 路径压缩 (2) 按秩合并 3. 并查集的应用 (1) 统计省份数量 (2) 判断等式方程是否成…
阅读更多...
JPA 基本查询（一）

JPA 基本查询（一）

JPA 查询简介示例 JPA教程 - JPA查询简介示例 最简单的JPQL查询选择单个实体类型的所有实例。 考虑下面的查询: SELECT e FROM Employee eJPQL尽可能使用SQL语法。 SQL查询从表中选择。JPQL从应用程序域模型的实体中选择。 语法 选择查询的整体形式如下: SELECT <sel…
阅读更多...
【操作系统1】一篇文章便可入门操作系统

【操作系统1】一篇文章便可入门操作系统

操作系统 (Operating System,OS)是一种系统软件&#xff0c;它负责管理计算机的硬件和软件资源。它的主要任务是组织和调度计算机的工作&#xff0c;并分配资源给用户和其他软件。操作系统为用户和软件提供了方便的接口和环境。它是计算机系统中最基本的软件之一。 一、操作系…
阅读更多...
μC/OS-Ⅱ源码学习(6)---事件标志组

μC/OS-Ⅱ源码学习(6)---事件标志组

快速回顾 μC/OS-Ⅱ中的多任务 μC/OS-Ⅱ源码学习(1)---多任务系统的实现 μC/OS-Ⅱ源码学习(2)---多任务系统的实现(下) μC/OS-Ⅱ源码学习(3)---事件模型 μC/OS-Ⅱ源码学习(4)---信号量 μC/OS-Ⅱ源码学习(5)---消息队列 本文进一步解析事件模型中&#xff0c;事件标志…
阅读更多...
【经验分享】OpenHarmony5.0.0-release编译RK3568不过问题(已解决)

【经验分享】OpenHarmony5.0.0-release编译RK3568不过问题(已解决)

问题描述 根据操作手册正常拉取代码&#xff0c;然后编译OpenHarmony5.0.0版本rk3568项目 编译命令 ./build.sh --product-name rk3568 --ccache出现如下报错 然后真正开始出错的位置是下面这句log FAILED: ../kernel/src_tmp/linux-5.10/boot_linux ../kernel/checkpoint/c…
阅读更多...
C++重点和练习-----多态

C++重点和练习-----多态

rpg.cpp: #include <iostream>using namespace std;/*模拟一个游戏场景有一个英雄&#xff1a;初始所有属性为1atk,def,apd,hp游戏当中有以下3种武器长剑Sword&#xff1a; 装备该武器获得 1atx&#xff0c;1def短剑Blade&#xff1a; 装备该武器获得 1atk&#xff0c;1…
阅读更多...
Qt之点击鼠标右键创建菜单栏使用（六）

Qt之点击鼠标右键创建菜单栏使用（六）

Qt开发 系列文章 - menu&#xff08;六&#xff09; 目录 前言 一、示例演示 二、菜单栏 1.MenuBar 2.Menu 总结 前言 QMainWindow是一个为用户提供主窗口程序的类&#xff0c;包含一个菜单栏&#xff08;menubar&#xff09;、多个工具栏(toolbars)、一个状态栏(status…
阅读更多...
天猫魔盒M17／M17S_超级UI 线刷固件包-可救砖（刷机取消双勾）

天猫魔盒M17／M17S_超级UI 线刷固件包-可救砖（刷机取消双勾）

在智能电视盒子的领域中&#xff0c;天猫魔盒 M17 以其独特魅力占据一席之地&#xff0c;然而&#xff0c;原厂设置有时难以满足进阶用户的多元需求。此刻&#xff0c;刷机成为开启全新体验的关键钥匙&#xff0c;为您的盒子注入鲜活能量。 一、卓越固件特性概览 此款精心打造的…
阅读更多...
Elasticsearch 7.x入门学习-Spring Data Elasticsearch框架

Elasticsearch 7.x入门学习-Spring Data Elasticsearch框架

1 Spring Data框架 Spring Data 是一个用于简化数据库、非关系型数据库、索引库访问&#xff0c;并支持云服务的开源框架。其主要目标是使得对数据的访问变得方便快捷&#xff0c;并支持 map-reduce 框架和云计算数据服务。 Spring Data 可以极大的简化 JPA的写法&#xff0c;…
阅读更多...
【落羽的落羽 C语言篇】一些常见的字符函数、字符串函数、内存函数

【落羽的落羽 C语言篇】一些常见的字符函数、字符串函数、内存函数

文章目录 一、字符函数1. 字符分类函数2. 字符转换函数 二、字符串函数1. strlen的使用和模拟实现使用模拟实现 2. strcpy的使用和模拟实现使用模拟实现 3. strcat的使用和模拟实现使用模拟实现 4. strcmp的使用和模拟实现使用模拟实现 5. strncpy的使用6. strncat的使用7. str…
阅读更多...
JAVA：访问者模式（Visitor Pattern）的技术指南

JAVA：访问者模式（Visitor Pattern）的技术指南

1、简述 访问者模式（Visitor Pattern）是一种行为型设计模式，允许你将操作分离到不同的对象中，而无需修改对象本身的结构。这种模式特别适合复杂对象结构中对其元素进行操作的场景。 本文将介绍访问者模式的核心概念、优缺点，并通过详细代码示例展示如何在实际应用中实现…
阅读更多...
小米自研系统Vela全面开源：开启物联网新时代的技术革新之旅

小米自研系统Vela全面开源：开启物联网新时代的技术革新之旅

目录 Vela系统的技术特点 1. 高性能与低功耗的完美平衡 2. 高度可扩展性与模块化设计 3. 强大的安全机制 4. 跨平台兼容性 Vela系统的应用场景 1. 智能家居领域 2. 工业物联网领域 3. 医疗健康领域 4. 智慧城市领域 Vela系统的深远影响 1. 推动物联…
阅读更多...
Linux/CentOS编译TensorFlow

Linux/CentOS编译TensorFlow

很多时候为了方便图省事&#xff0c;是通过pip安装TensorFlow的&#xff0c;然而很不幸运行的服务器不支持AVX指令&#xff0c;引入模块的时候会报错&#xff1a; The TensorFlow library was compiled to use AVX instructions, but these aren’t available on your machine.…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023