1. 矩阵乘法 Matrix multiplication

我们通过四种方法讨论如何使矩阵A与B相乘得到矩阵C。其中A为mxn（m行n列）矩阵，而B为nxp矩阵，则C为mxp矩阵，记cij为矩阵C中第i行第j列的元素

1.1 Regular way

矩阵乘法的标准计算方法是通过矩阵A第i行的行向量和矩阵B 第j列的列向量点积得到cij

eg.

1.2 Column way

列操作是指矩阵C的第j列是通过矩阵A乘以矩阵B第j列的列向量得到的。这表明矩阵C的列向量是矩阵A列向量的线性组合，组合的“权”就是矩阵B第j列的各个分量 

Column of C are combinations of columns of A

1.3 Row way

行操作是指矩阵C的第i行是通过矩阵A的第i行乘以矩阵B得到的。这表明矩阵C的行向量是矩阵B行向量的线性组合

Rows of C are combinations of rows of B

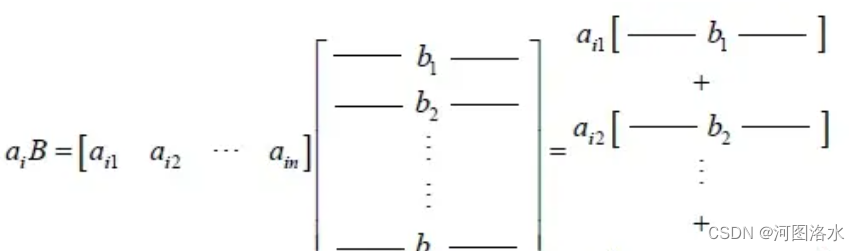
1.4 column of A × row of B

矩阵A的第k列是一个m1的向量，而矩阵B第k行是一个1p的向量，两向量相乘会得到一个矩阵Ck，将所有的n个矩阵相加记得到C

AB = sum of (cols of A) × (rows of B)

eg.

1.5 Block multiplication

C1=A1B1+A2B3

2. 逆矩阵 Inverse

如果矩阵A是方阵(square matrices)，若存在逆矩阵 ，使得A=I=A （左逆矩阵等于右逆矩阵）。我们称矩阵A可逆（invertible）或者矩阵A非奇异（nonsingular）

反之，如果A为奇异（singular），则其没有逆矩阵。它的行列式为0。另一个等价的说法是，A为奇异阵，则方程Ax=0存在非零解x 

i can find a vector X with AX=0

eg:

在这个二阶矩阵的例子中，两个列向量排列在同一方向上。不可逆矩阵中总有列向量对生成线性组合没有贡献，等价的说法还有：不可逆矩阵的列向量可以通过线性组合得到0

3. 高斯-若尔当消元法 Gauss-Jordan Elimination

A × column j of  = column j of I

Gauss-Jordan solves 2 equas at once

在用高斯消元法的到上三角矩阵之后，按照若尔当的做法继续消元，用第一行减去第二行的若干倍，最后原矩阵变为单位阵，这时右侧的矩阵即为逆矩阵

Gauss-Jordan Elimination

对A进行一系列消元操作，相当于左乘消元矩阵E，此时消元的结果为EA=I，因为右侧矩阵也进行了同样消元操作，也等于左乘矩阵E，则右侧矩阵为EI=E。由EA=I 可知这里的E就是A的逆矩阵

EA = I tells us E=