
摘要
本文提出了一种基于区间观测器的故障诊断与容错控制方法。该方法通过构建区间观测器,实现对系统状态的上下边界估计,从而在存在不确定性和外部噪声的情况下进行高效的故障诊断。进一步地,本文设计了一种容错控制策略,以保证系统在发生故障时仍能稳定运行。仿真结果表明,该方法能够准确诊断故障并有效提高系统的鲁棒性。
理论
1. 区间观测器概述
区间观测器是一种基于不确定性边界的观测器,它在已知系统模型与噪声上下界的条件下,利用输入输出数据估计系统状态。区间观测器通过构建状态的上下界,能够提供保守但鲁棒的状态估计。
假设系统模型为:

区间观测器形式为:
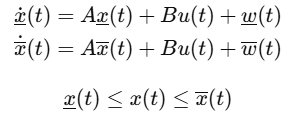
2. 容错控制策略
容错控制策略利用区间观测器提供的状态估计结果,根据故障模式设计补偿控制律,从而减小故障对系统的影响。容错控制目标是保证故障发生后系统状态仍能满足稳定性要求。
实验结果
实验在MATLAB中进行,仿真验证了区间观测器的有效性及容错控制策略的鲁棒性。
-
图1 展示了系统状态的真实值及其上下界,验证了区间观测器在有噪声干扰下的有效性。
-
图2 显示了噪声的波动情况,噪声模型符合随机白噪声特性。
实验结果表明:
区间观测器能够准确估计状态边界。 容错控制策略能够在不同故障模式下有效补偿,并保持系统稳定。

部分代码
% 系统参数设置
A = [0 1; -2 -3];
B = [0; 1];
C = [1 0];
w_bound = 0.1; % 过程噪声上下界
v_bound = 0.05; % 测量噪声上下界
t = 0:0.01:2; % 仿真时间% 区间观测器初始化
x_real = zeros(2, length(t)); % 实际状态
x_real(:, 1) = [5; -2];
x_hat_lower = x_real(:, 1) - 0.5; % 初始下界
x_hat_upper = x_real(:, 1) + 0.5; % 初始上界% 噪声生成
w_noise = w_bound * (2*rand(size(t)) - 1);
v_noise = v_bound * (2*rand(size(t)) - 1);% 仿真主循环
for i = 2:length(t)% 实际系统动态u = sin(t(i)); % 控制输入x_real(:, i) = x_real(:, i-1) + (A * x_real(:, i-1) + B * u) * (t(i) - t(i-1)) + [w_noise(i-1); 0];% 区间观测器更新x_hat_lower(:, i) = x_hat_lower(:, i-1) + (A * x_hat_lower(:, i-1) + B * u + [-w_bound; 0]) * (t(i) - t(i-1));x_hat_upper(:, i) = x_hat_upper(:, i-1) + (A * x_hat_upper(:, i-1) + B * u + [w_bound; 0]) * (t(i) - t(i-1));
end% 结果可视化
figure;
subplot(2,1,1);
plot(t, x_real(1,:), 'b', 'LineWidth', 1.5); hold on;
plot(t, x_hat_lower(1,:), 'r--');
plot(t, x_hat_upper(1,:), 'r--');
title('State x_1 and its bounds');
legend('x_1', 'Lower bound', 'Upper bound');subplot(2,1,2);
plot(t, x_real(2,:), 'b', 'LineWidth', 1.5); hold on;
plot(t, x_hat_lower(2,:), 'r--');
plot(t, x_hat_upper(2,:), 'r--');
title('State x_2 and its bounds');
legend('x_2', 'Lower bound', 'Upper bound');% 噪声图
figure;
plot(t, w_noise);
title('White noise w(t)');
xlabel('t / s');
ylabel('Value of white noise');
参考文献
❝
Blanchini, F., & Miani, S. (2008). Set-theoretic methods in control. Springer Science & Business Media.
Tanaka, K., & Wang, H. O. (2001). Fuzzy control systems design and analysis: a linear matrix inequality approach. John Wiley & Sons.
Chen, J., & Patton, R. J. (2012). Robust model-based fault diagnosis for dynamic systems. Springer Science & Business Media.
(文章内容仅供参考,具体效果以图片为准)



















