完全背包动态规划 + 一维dp数组

动态规划：完全背包理论基础

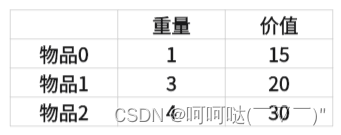
每件商品都有无限个！！！

（1）0-1背包的核心代码

解决0-1背包问题（方案二）：一维dp数组（滚动数组）_呵呵哒(￣▽￣)"的博客-CSDN博客

for(int i = 0;i < weight.size(); i++) { // 遍历物品for(int j = bagWeight;j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);}
}

（2）完全背包的核心代码

// 先遍历物品，再遍历背包
for(int i = 0;i < weight.size(); i++) { // 遍历物品for(int j = weight[i];j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);}
}

请问😚0-1背包和完全背包有什么区别呢？

有，0-1背包问题中的背包容量是从大到小去遍历的，完全背包问题中的背包容量是从小到大去遍历的。

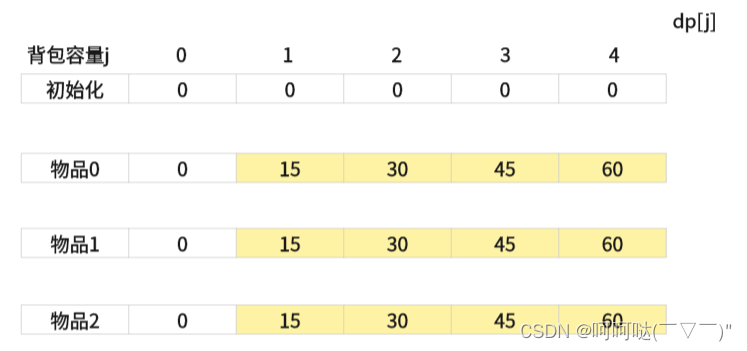
思考🤔：请问在完全背包中，对于一维dp数组来说，两个for循环嵌套顺序不同，结果还一样吗？

回答：一样！

（1）遍历物品在外层循环，遍历背包容量在内层循环

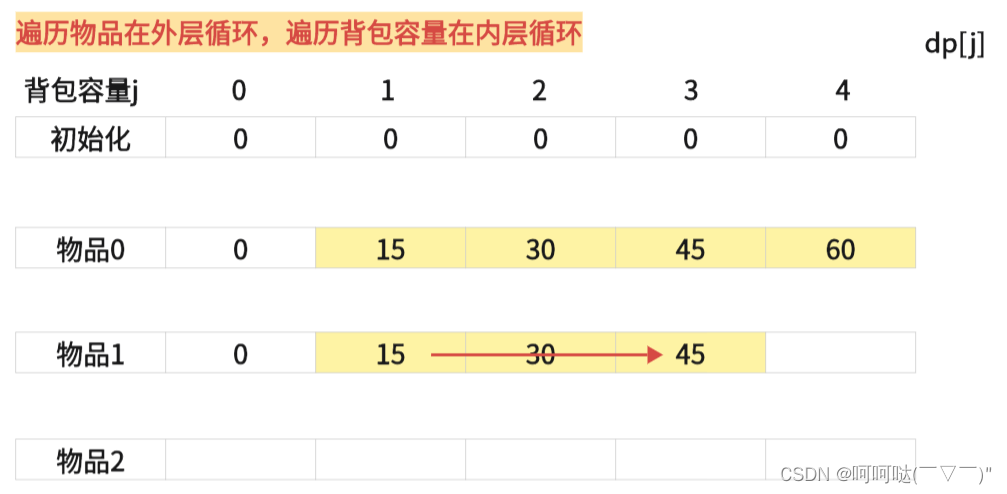
（2）遍历背包容量在外层循环，遍历物品在内层循环

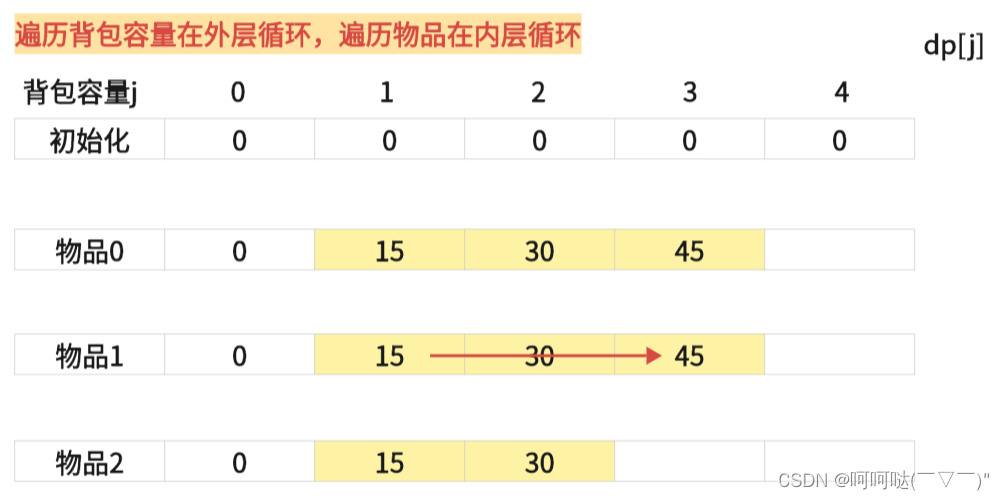
也就是说，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）

完全背包的核心代码
// 先遍历物品，再遍历背包
for(int i = 0;i < weight.size(); i++) { // 遍历物品for(int j = weight[i];j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);}
}// 先遍历背包，再遍历物品
for(int j=0;j <= bagWeight;j++) { // 遍历背包容量for(int i=0;i < weight.size(); i++) { // 遍历物品if(j-weight[i] >= 0) dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);}
}

完整测试代码：

#include <iostream>
using namespace std;
#include <vector>// 先遍历物品，再遍历背包
void test_CompletePack() {vector<int> weight = { 1,3,4 };vector<int> value = { 15,20,30 };int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < weight.size(); i++) { // 遍历物品for (int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}// 先遍历背包，再遍历物品
void test_CompletePack() {vector<int> weight = { 1,3,4 };vector<int> value = { 15,20,30 };int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for (int j = 0; j <= bagWeight; j++) { // 遍历背包容量for (int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0)dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}int main() {test_CompletePack();return 0;
}

来自代码随想录的文字摘取：代码随想录 (programmercarl.com)

总结：对于纯完全背包问题，其for循环的先后循环是可以颠倒的！！！