决策过程
- 0. 前言
- 1.决策过程的引入
- 1.1有了planning,为什么还需要decision-making?
- 1.2 决策规划的一些思考
- 2.马尔可夫决策过程及其关键要素
- 2.1 马尔可夫过程
- 2.1.1 什么是随机过程?
- 2.1.2 什么是马尔科夫性?
- 2.1.3 马尔可夫决策过程 (MDP)
- 2.1.4 决策问题要素
- 2.1.5 决策问题要素:以无保护左转为例
- 2.1.6 策略定义(Policy)
- 2.1.7 MDP目标和策略
- 2.1.8 无保护左转场景示例
- MDP的目标及策略定义
- 贝尔曼方程求解过程
- 简单代码实现
- 2.2 价值迭代与策略迭代
- 2.2.1 价值迭代
- 价值迭代(Value Iteration)的解释
- 价值迭代的伪代码
- 主要的难点和瓶颈
- 2.2.2 价值迭代举例
- Gridworld说明
- 迭代过程
- 迭代1次后的结果
- 迭代2次后的结果
- 迭代3次后的结果
- 1000次迭代后,趋于稳定
- 自动驾驶场景举例
- 2.2.3 策略迭代
- 基本概念
- 策略迭代举例
- 3. 参考
0. 前言
本文主要记录课程《自动驾驶预测与决策技术》的学习过程,难免会有很多纰漏,感谢指正。
课程链接:https://www.shenlanxueyuan.com/my/course/700
相关笔记链接:
Part1_自动驾驶决策规划简介
Part2_基于模型的预测方法
Part3_路径与轨迹规划
Part4_时空联合规划
1.决策过程的引入
1.1有了planning,为什么还需要decision-making?
keypoint:交互、不确定性
Geometric World(几何世界)–> Probabilistic World(概率世界),几何世界关注的是空间的静态性质,而概率世界关注的是动态的、不确定的过程。
在自动驾驶系统中,planning(规划)和decision-making(决策)虽然紧密相关,但它们各自扮演着不同的角色,都是确保自动驾驶车辆安全、高效运行的重要组成部分。
a.Planning(规划)
规划通常指的是自动驾驶系统中的路径规划功能。它的核心任务是基于车辆的当前位置、目标位置以及周围环境信息,生成一条从起点到终点的最优路径。这包括:
-
全局路径规划:在高层次上,规划出从起点到目标地点的最佳路径,这可能涉及跨越多个道路段、交叉口等。
-
局部路径规划:在每个时刻,根据当前环境和交通状况,调整并优化行驶路径。这通常涉及对最近几米至几百米的路线进行细化处理。
-
避障:处理动态障碍物(如行人、其他车辆)和静态障碍物(如路障)的问题,确保路径的安全性和有效性。
b.Decision-Making(决策)
决策涉及在复杂的交通环境中做出具体的驾驶决策。这包括:
-
交通规则遵循:遵守交通信号灯、标志、限速等规则。
-
交互决策:与其他交通参与者的互动,例如在复杂交叉口时如何选择合适的行驶策略,或者如何应对突发状况(如另一辆车突然变道)。
-
优先级处理:决定在某些情况下的优先权问题,比如在遇到紧急车辆时的让行策略。
c.为什么都需要?
-
复杂性和动态性:虽然路径规划可以为车辆提供一条理想的路线,但现实世界中情况复杂且不断变化。决策系统需要实时处理各种动态因素,如其他车辆的行为、交通信号的变化等。
-
安全性:决策系统确保车辆在实际道路上安全行驶,通过对各种复杂情况的判断,调整规划结果以应对意外和突发事件。
-
交通规则和法规:规划可能无法完全满足所有交通规则的要求,决策系统负责确保车辆在遵守交通法规的同时执行适当的行驶策略。
-
用户体验:决策系统可以优化驾驶体验,使得车辆在各种情况下能够平稳、舒适地运行,而不仅仅是按照静态的路径规划进行行驶。
d.总结
- 规划主要关注从起点到目标的静态路径生成,适合处理较为稳定和已知的环境,但对于动态和复杂的情况适应性较差。
- 决策则侧重于实时应对不确定性和动态变化,确保车辆在实际行驶过程中能够适应各种突发情况和环境变化,从而更灵活地实现目标。
1.2 决策规划的一些思考
在运动规划和控制模块的基础上,为什么还需要决策过程?

每个障碍物有一定的不确定性,且对手车也会根据自车的决策做出不同的action。
每种方案实际上对应一种决策,每种决策实际上对应一簇规划。
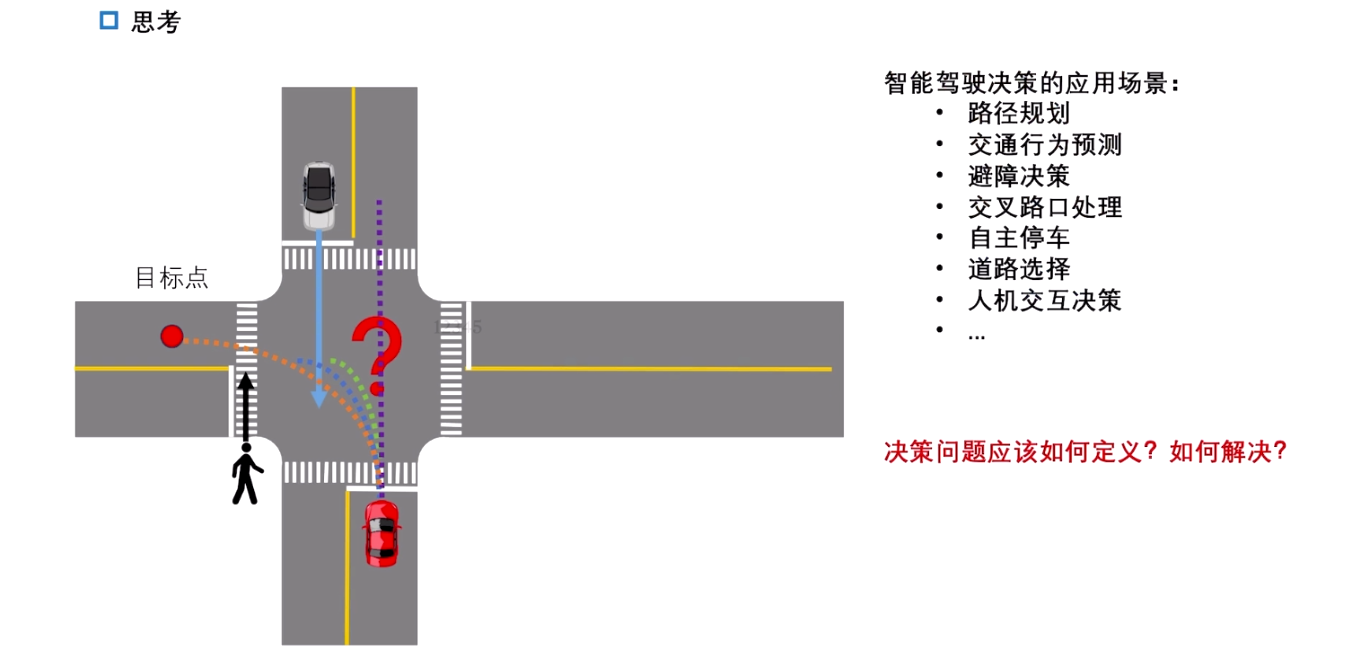
智能驾驶决策的应用场景:路径规划、交通行为预测、避障决策、交叉路口处理、自主停车、道路选择等等。
关键问题:决策问题如何定义,决策空间如何求解?
2.马尔可夫决策过程及其关键要素
2.1 马尔可夫过程

2.1.1 什么是随机过程?
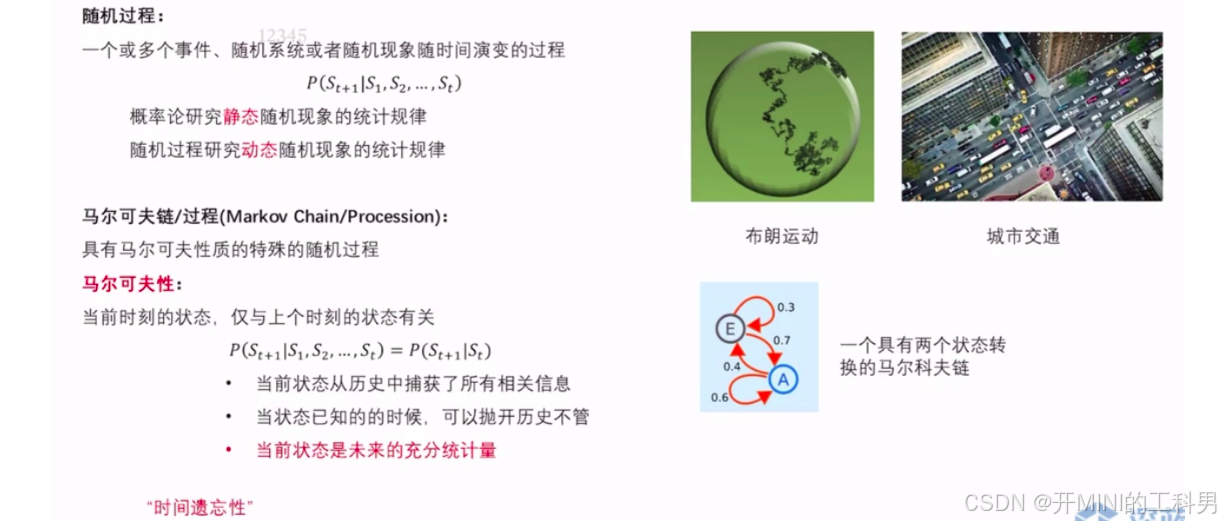
随机过程(Stochastic Process)是一个数学对象,它描述了一个系统的状态如何随着时间演变,其中系统的状态是随机的。具体来说,随机过程是一个随时间变化的随机变量的集合,每个时间点都有一个对应的随机变量。
-
状态空间:
- 随机过程的状态空间是系统可能的所有状态的集合。状态空间可以是离散的(如有限个状态的集合)或连续的(如实数集)。
-
时间参数:
- 随机过程可以在离散时间或连续时间上定义。离散时间随机过程在一系列离散的时间点上定义状态(如每天、每月),而连续时间随机过程在连续的时间段内定义状态(如每秒钟)。
-
样本路径:
- 随机过程的一个可能的状态序列称为样本路径或轨迹。每个样本路径表示在给定随机过程下系统可能的行为模式。
-
典型例子:
- 布朗运动(Brownian Motion):一种描述粒子在液体或气体中随机运动的过程。
- 马尔科夫链(Markov Chain):状态转移只依赖于当前状态而与过去无关的离散时间随机过程。
- 泊松过程(Poisson Process):用于描述稀疏事件的到达时间,如电话呼叫的到达或事故发生的次数。
2.1.2 什么是马尔科夫性?
马尔科夫性(Markov Property)是指一个过程的未来状态只依赖于当前状态,而与过去的历史状态无关。这个概念源自于马尔科夫过程(Markov Process),它在概率论和统计学中扮演着重要角色。
-
定义:
- 马尔科夫性强调的是记忆无关性(memorylessness)。即系统的未来状态只取决于当前状态,而不依赖于系统的过去状态。
- 形式上,对于一个马尔科夫过程,给定当前状态 ( S t S_t St),未来状态 ( S t + 1 S_{t+1} St+1) 的条件概率分布不依赖于过去的状态序列 ( S t − 1 , S t − 2 , … , S 0 S_{t-1}, S_{t-2}, \ldots, S_0 St−1,St−2,…,S0)。
-
数学表示:
- 设 ( { S t } t ≥ 0 \{S_t\}_{t \geq 0} {St}t≥0) 为一个随机过程,若对所有的 ( t ≥ 0 t \geq 0 t≥0) 和所有的状态 ( s 0 , s 1 , … , s t , s t + 1 s_0, s_1, \ldots, s_t, s_{t+1} s0,s1,…,st,st+1),有:
P ( S t + 1 = s t + 1 ∣ S t = s t , S t − 1 = s t − 1 , … , S 0 = s 0 ) = P ( S t + 1 = s t + 1 ∣ S t = s t ) P(S_{t+1} = s_{t+1} \mid S_t = s_t, S_{t-1} = s_{t-1}, \ldots, S_0 = s_0) = P(S_{t+1} = s_{t+1} \mid S_t = s_t) P(St+1=st+1∣St=st,St−1=st−1,…,S0=s0)=P(St+1=st+1∣St=st)
则称该过程具有马尔科夫性。
- 设 ( { S t } t ≥ 0 \{S_t\}_{t \geq 0} {St}t≥0) 为一个随机过程,若对所有的 ( t ≥ 0 t \geq 0 t≥0) 和所有的状态 ( s 0 , s 1 , … , s t , s t + 1 s_0, s_1, \ldots, s_t, s_{t+1} s0,s1,…,st,st+1),有:
-
类型:
- 离散时间马尔科夫链(Discrete-Time Markov Chain):在离散时间步骤中发生的马尔科夫过程,状态的转移依赖于当前状态和固定的转移概率矩阵。
- 连续时间马尔科夫过程(Continuous-Time Markov Process):在连续时间中发生的马尔科夫过程,状态的转移通常由到达率(或强度)来描述。
2.1.3 马尔可夫决策过程 (MDP)
马尔科夫决策过程(Markov Decision Process, MDP)是一种用于描述和解决涉及决策的随机过程的数学框架,常用于优化决策策略。在MDP中,决策者在每个时间步骤选择一个行动,根据所选行动和当前状态,系统转移到一个新的状态,并获得相应的奖励。
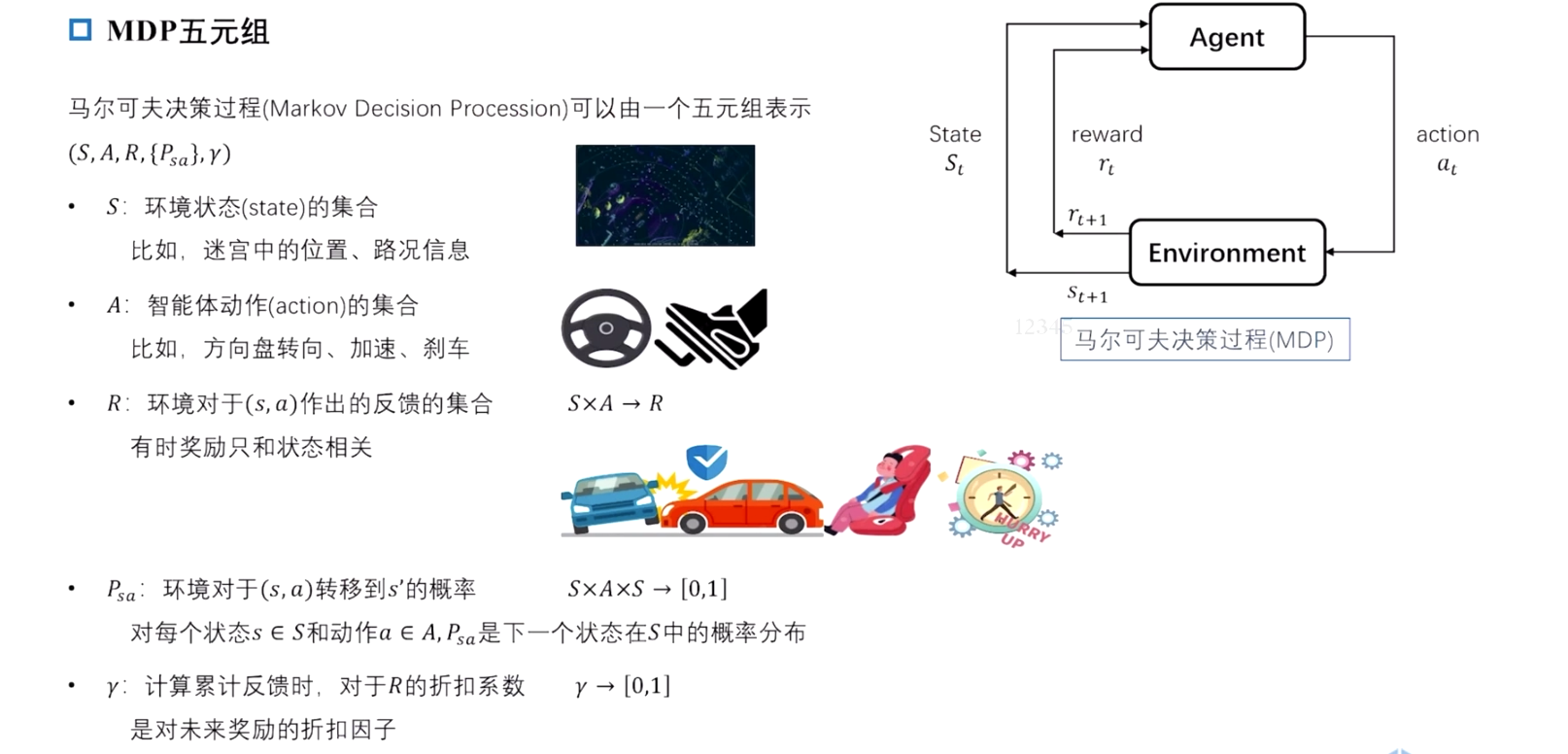
关键要素
-
状态空间( S t a t e S p a c e State Space StateSpace):
- 设 ( S S S ) 为所有可能状态的集合。系统在每个时间步骤都处于状态 ( s ∈ S s \in S s∈S )。
-
动作空间( A c t i o n S p a c e Action Space ActionSpace):
- 设 ( A A A) 为所有可能动作的集合。决策者可以在每个状态下选择一个动作 ( a ∈ A a \in A a∈A)。
-
转移概率( T r a n s i t i o n P r o b a b i l i t y Transition Probability TransitionProbability):
- 转移概率 ( P ( s ′ ∣ s , a ) P(s' \mid s, a) P(s′∣s,a)) 表示在当前状态 ( s s s) 下采取动作 ( a a a ) 后转移到状态 ( s ′ s' s′) 的概率。
-
奖励函数( R e w a r d F u n c t i o n Reward Function RewardFunction):
- 奖励函数 ( R ( s , a ) R(s, a) R(s,a)) 表示在状态 ( s s s ) 下采取动作 ( a a a) 所获得的即时奖励。
-
策略( P o l i c y Policy Policy):
- 策略 ( π \pi π) 是一个映射,将每个状态 ( s s s) 映射到一个动作 ( a a a)。策略可以是确定性的(即在每个状态下选择一个特定的动作)或随机的(即在每个状态下选择动作的概率分布)。
-
价值函数( V a l u e F u n c t i o n Value Function ValueFunction):
- 状态价值函数 ( V π ( s ) V^\pi(s) Vπ(s)) 表示在策略 ( π \pi π) 下,从状态 ( s s s) 开始的预期总奖励。
- 动作价值函数 ( Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)) 表示在策略 ( π \pi π) 下,从状态 ( s s s) 开始采取动作 ( a a a) 的预期总奖励。
目标
在MDP中,决策者的目标通常是找到一个最优策略 ( π ∗ \pi^* π∗),使得从任何状态 ( s s s) 开始的预期总奖励最大化。这个最优策略可以通过以下方法求解:
- 动态规划:使用贝尔曼方程(Bellman Equation)递归地计算价值函数。
- 强化学习:通过与环境的交互来学习最佳策略,如Q学习(Q-learning)和策略梯度方法(Policy Gradient Methods)。
2.1.4 决策问题要素
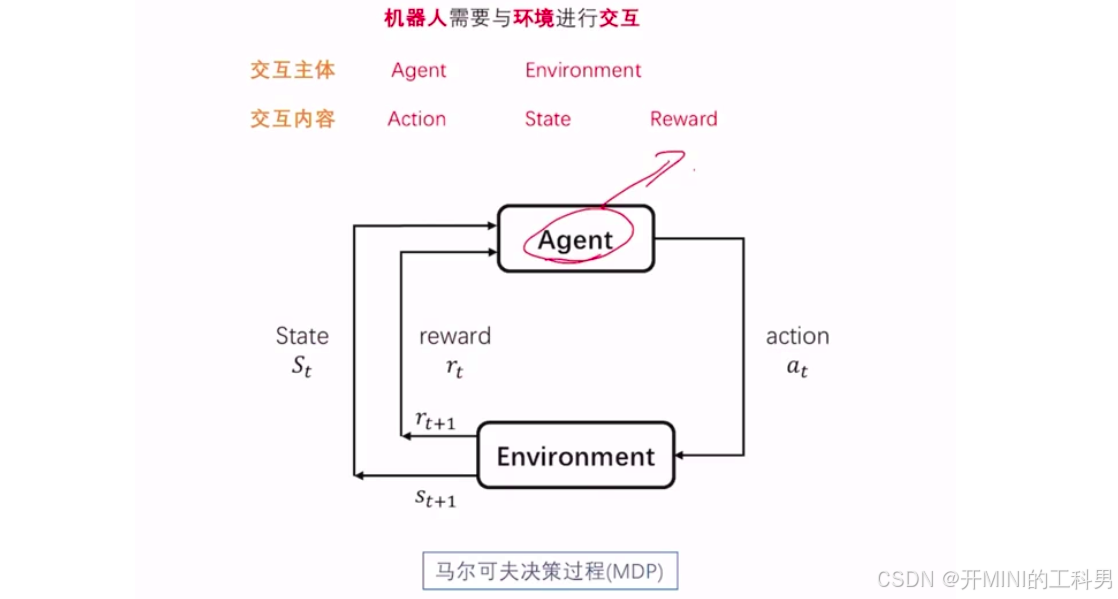
交互主体: Agent、Environment
交互内容:Action、 State、Reward
MDP 五元组
马尔可夫决策过程(MDP)在自动驾驶中的使用可以帮助自动驾驶系统做出最佳的驾驶决策。MDP 可通过以下五个关键元素来描述决策过程的:
- 状态集合 ( S S S ):代表环境的所有可能状态。在自动驾驶中,状态可以包括车辆的位置、速度、道路状况、周围车辆和行人的位置等。
- 动作集合 ( A A A):代表系统可以采取的所有可能动作。在自动驾驶中,这些动作可以包括加速、刹车、转向等。
- 奖励函数 ( R R R):对于每一个状态-动作对 ( ( s , a ) (s, a) (s,a)),奖励函数定义了执行该动作后的即时奖励。在自动驾驶中,奖励可以反映驾驶的安全性、舒适性、效率等,例如避开碰撞、保持车道、减少油耗等。
- 状态转移概率 ( P s a P_{sa} Psa):定义了在当前状态 ( s s s) 下采取动作 ( a a a ) 后转移到下一个状态 ( s ′ s' s′ ) 的概率分布。在自动驾驶中,这个概率可以表示在不同路况下,不同驾驶动作的结果。例如,在湿滑路面上,转向的结果可能不如在干燥路面上那么可预测。
- 折扣因子 ( γ \gamma γ):用于计算累积奖励的折扣因子,反映未来奖励的相对重要性。折扣因子通常用于平衡短期和长期的奖励。
在自动驾驶中的具体使用:
- 感知和建模环境:自动驾驶系统首先通过传感器感知环境,识别当前的状态 ( s t s_t st)。
- 策略选择:系统根据当前状态 ( s t s_t st) 和决策策略(通常是通过强化学习训练得出)选择一个动作 ( a t a_t at),如转向、加速或刹车。
- 执行动作并反馈:系统执行选择的动作,并通过感知更新环境状态 ( s t + 1 s_{t+1} st+1)。同时,系统会得到即时的奖励 ( r t r_t rt )。
- 学习和优化:系统通过不断地进行状态-动作-奖励-新状态的循环,从而学习最优策略,以最大化累积奖励。
关键应用场景:
- 路径规划:MDP 可以帮助自动驾驶车辆在复杂的道路环境中规划出一条最优路径,同时避免障碍物、遵循交通规则。
- 避障:在动态环境中,例如有行人或其他车辆突然出现时,MDP 帮助系统快速做出安全的决策。
- 驾驶行为优化:MDP 可以用于优化驾驶行为,如节能驾驶或平稳驾驶,从而提高乘坐体验和车辆效率。
MDP 的动态过程
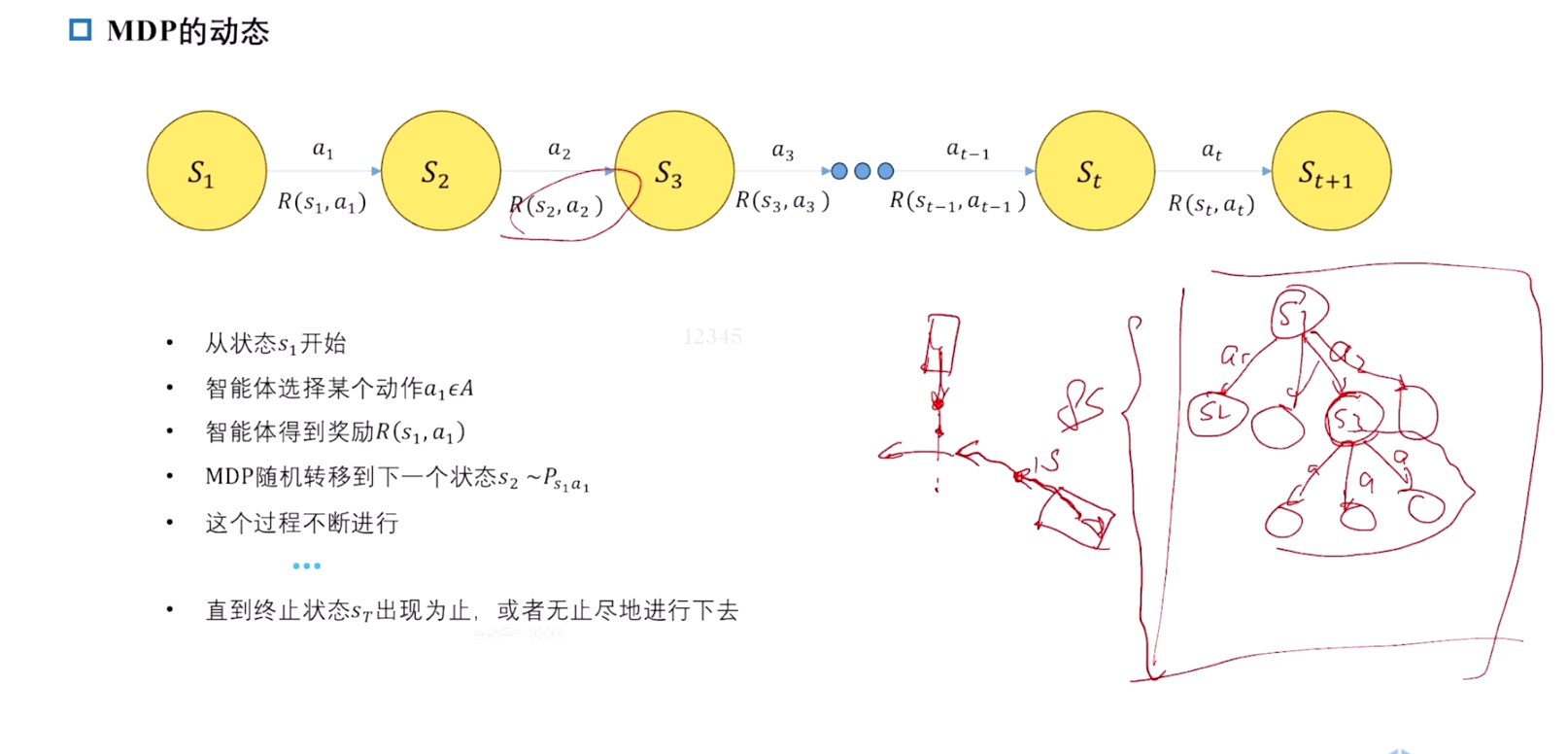
2.1.5 决策问题要素:以无保护左转为例
无保护左转是指在没有专用信号灯保护的情况下,车辆需要在流动的对向车流中找到合适的时机进行左转。这是自动驾驶中的一个复杂场景,要求系统能够在动态环境中做出及时且安全的决策。
状态集合 ( S S S )
在无保护左转的场景中,状态集合包括车辆自身的位置和速度、对向车流的状况(如对向车辆的速度和距离)、路口的几何信息(如车道宽度、信号灯状态)、行人和其他潜在的障碍物。
动作集合 ( A A A )
在这个场景下的动作集合包括:
- 等待(保持当前位置不动)
- 开始左转(根据环境情况调整转向角度和速度)
- 适时停止或减速(在发现潜在危险时停止或减速)
奖励函数 ( R R R)
奖励函数在无保护左转中主要考虑以下因素:
- 正向奖励:成功完成左转,或者在合适时机内安全完成左转。
- 负向奖励:发生危险行为,如与对向车辆过于接近、紧急刹车、或者不得不在危险情况下强行左转。
奖励函数会根据这些因素给予相应的奖励或惩罚。
状态转移概率 ( P s a P_{sa} Psa)
状态转移概率描述了在执行某个动作后,环境状态如何变化。对于无保护左转,系统需要根据对向车辆的速度和距离、行人的动态行为、以及自身动作的效果(如加速、转向),预测下一个可能的状态。例如:
- 如果对向车流速度较慢且距离较远,左转可能是安全的,系统会转移到成功完成左转的状态。
- 如果对向车流突然加速或有车辆突然出现,系统可能需要重新评估是否继续左转,或者进入紧急停止的状态。
折扣因子 ( γ \gamma γ)
折扣因子在这里用于平衡短期与长期的决策。例如,系统可能会更关注即刻的安全性(短期奖励),而不是过于冒险以求快速完成左转(长期奖励)。通常折扣因子会设定在一个相对较高的值,以确保系统优先考虑立即的安全。
动态过程描述
-
初始状态识别:
车辆接近路口,自动驾驶系统通过感知模块识别当前状态 ( S 0 S_0 S0),包括自身的位置、速度,对向车流的状况以及路口的结构信息。 -
策略选择:
系统通过计算,在当前状态下选择最优动作 ( A 0 A_0 A0)。假设此时对向车流较密,系统选择保持等待状态,继续观察对向车流的变化。 -
状态更新:
随着对向车辆的变化(如某辆车减速或通过路口),状态 ( S 1 S_1 S1) 更新。系统重新评估并选择新的动作 ( A 1 A_1 A1),例如开始缓慢左转。 -
动作执行与反馈:
系统执行左转动作,并实时监控对向车流和自身车辆的动态。此时,如果检测到安全,系统会继续加速完成左转;否则,会减速或停止,以避免碰撞。 -
迭代决策:
在整个过程中,系统不断地根据新的感知数据更新状态,迭代地选择最优动作,直到成功完成左转或决定暂停操作以等待更好的机会。 -
奖励评估:
一旦左转完成,系统根据整个过程中的决策结果计算最终的奖励。如果操作安全且顺利完成,系统将获得正向奖励;如果中途出现危险操作或需要紧急避险,则相应地减少奖励。
2.1.6 策略定义(Policy)
确定型策略求解 --> 三板斧:采样、搜索、优化
随机型策略求解:MDP/POMDP --> Bellman 原理 --> optimal solution --> reward 奖励函数
以无保护左转为例:
在无保护左转的场景中,随机型策略(Stochastic Policy) 是指在每一个状态下,自动驾驶系统不确定地选择动作,而是根据某种概率分布来选择动作。与确定性策略(每个状态下只选择一个固定动作)不同,随机型策略允许系统在同一个状态下有多个可能的动作选择,每个动作都有一定的概率。
- 随机型策略的定义
随机型策略通常用 ( π ( a ∣ s ) \pi(a|s) π(a∣s)) 表示,它定义了在状态 ( s ) s) s) 下选择动作 ( a a a) 的概率分布。对于无保护左转场景,策略 ( π ( a ∣ s ) \pi(a|s) π(a∣s)) 可以这样理解:
- 在特定状态 ( s s s ) 下(如车辆正在接近路口,且对向车流较稀疏),策略可能定义以下概率分布:
- 等待 ( a 1 a_1 a1): ( π ( a 1 ∣ s ) = 0.3 \pi(a_1|s) = 0.3 π(a1∣s)=0.3 )(30% 的概率保持等待)
- 左转 ( a 2 a_2 a2): ( π ( a 2 ∣ s ) = 0.7 \pi(a_2|s) = 0.7 π(a2∣s)=0.7 )(70% 的概率尝试左转)
这种随机性允许系统在相似的状态下尝试不同的动作,探索不同的策略组合。
- 求解随机型策略
求解随机型策略通常依赖于强化学习中的策略梯度方法或动态规划方法。这里介绍一些常见的求解方法:
a. 策略梯度方法
策略梯度方法直接优化策略的参数化表示,通常用于深度强化学习场景。它通过最大化累计奖励的期望来更新策略参数。
-
策略参数化:假设策略由参数 ( θ \theta θ) 表示,即 ( π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s)) 是依赖于参数 ( θ \theta θ ) 的概率分布。
-
目标函数:定义累积奖励的期望 ( J ( θ ) = E π θ [ R ] J(\theta) = \mathbb{E}_{\pi_{\theta}} [R] J(θ)=Eπθ[R]),其中 ( R ) R) R) 是累积奖励。目标是最大化 ( J ( θ ) J(\theta) J(θ))。
-
策略梯度:使用策略梯度算法(如 REINFORCE 算法)更新参数:
θ ← θ + α ∇ θ J ( θ ) \theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta) θ←θ+α∇θJ(θ)
其中,( α \alpha α ) 是学习率,梯度 ( ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)) 可以通过样本估计得到。 -
更新策略:每次通过梯度上升方法更新参数 ( θ \theta θ ),并调整策略 ( π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s)),使得在状态 ( s s s ) 下选择最优动作的概率更高。
b. 动态规划方法
如果状态和动作空间有限,且有已知的模型(如状态转移概率 ( P s a ) P_{sa} ) Psa)),可以使用动态规划方法求解最优随机型策略。
-
贝尔曼方程:构建贝尔曼期望方程,描述状态值函数 ( V π ( s ) ) V^{\pi}(s) ) Vπ(s)):
V π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ P s a ( s ′ ) [ R ( s , a , s ′ ) + γ V π ( s ′ ) ] V^{\pi}(s) = \sum_{a} \pi(a|s) \sum_{s'} P_{sa}(s') \left[ R(s, a, s') + \gamma V^{\pi}(s') \right] Vπ(s)=a∑π(a∣s)s′∑Psa(s′)[R(s,a,s′)+γVπ(s′)]
或者动作值函数 ( Q π ( s , a ) Q^{\pi}(s, a) Qπ(s,a)):
Q π ( s , a ) = ∑ s ′ P s a ( s ′ ) [ R ( s , a , s ′ ) + γ ∑ a ′ π ( a ′ ∣ s ′ ) Q π ( s ′ , a ′ ) ] Q^{\pi}(s, a) = \sum_{s'} P_{sa}(s') \left[ R(s, a, s') + \gamma \sum_{a'} \pi(a'|s') Q^{\pi}(s', a') \right] Qπ(s,a)=s′∑Psa(s′)[R(s,a,s′)+γa′∑π(a′∣s′)Qπ(s′,a′)]
或者动作值函数 ( Q π ( s , a ) Q^{\pi}(s, a) Qπ(s,a)): -
策略迭代:通过以下步骤反复进行:
- 策略评估:在当前策略 ( π \pi π) 下,计算状态值函数 ( V π ( s ) V^{\pi}(s) Vπ(s)) 或动作值函数 ( Q π ( s , a ) ) Q^{\pi}(s, a)) Qπ(s,a))。
- 策略改进:根据状态值或动作值函数更新策略 ( π \pi π ),以增加最优动作的选择概率。
- 收敛条件:策略迭代直至策略收敛,即不再有改进为止,得到的策略即为最优随机型策略。
在无保护左转场景中的应用
-
策略探索:随机型策略允许系统在类似状态下探索不同的左转决策,从而避免因单一策略可能导致的潜在问题,例如过于保守或过于激进的驾驶行为。
-
风险管理:在高风险场景下(如对向车流密集),随机型策略可以分配一定的概率给“等待”动作,从而减少因冒险左转可能带来的风险。
2.1.7 MDP目标和策略
目标:选择能够最大化累积奖励期望的动作
奖励函数 R
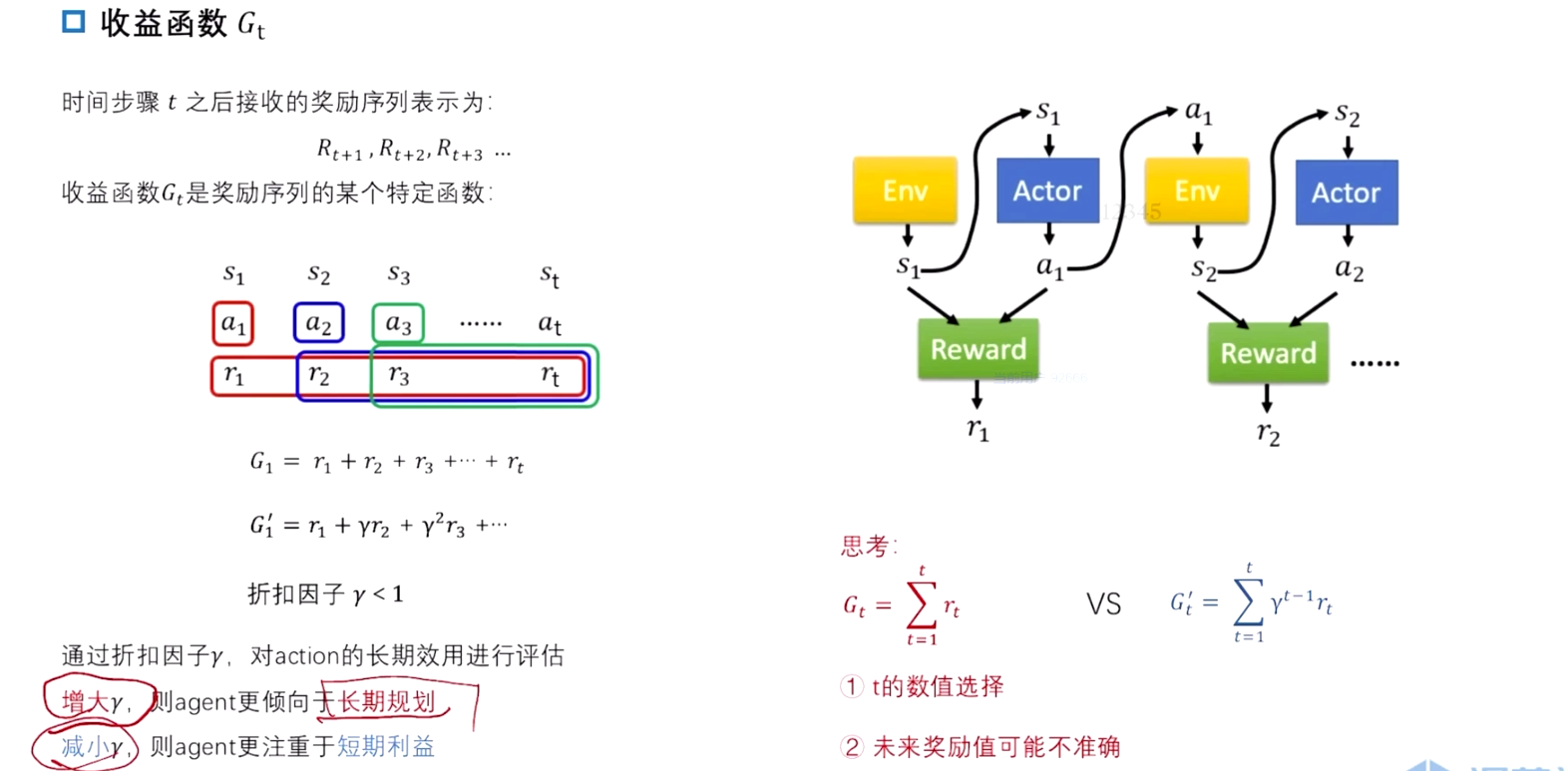
收益函数 Gt
奖励函数的时间序列

动作价值函数

2.1.8 无保护左转场景示例
在无保护左转场景中,使用不确定型(随机型)策略的马尔可夫决策过程(MDP)可以帮助自动驾驶系统应对环境中的不确定性。、
-
MDP的目标及策略定义
MDP的目标
MDP的目标是最大化期望累计奖励,即使得车辆在无保护左转过程中,尽可能成功地完成左转并避免事故。公式化的目标函数为:
maximize E π [ G 0 ] = E π [ ∑ t = 0 ∞ γ t R t + 1 ] \text{maximize} \quad \mathbb{E}_{\pi} \left[ G_0 \right] = \mathbb{E}_{\pi} \left[ \sum_{t=0}^{\infty} \gamma^t R_{t+1} \right] maximizeEπ[G0]=Eπ[t=0∑∞γtRt+1]
其中:- ( E π \mathbb{E}_{\pi} Eπ ) 是在策略 ( $\pi $) 下的期望值。
- ( G 0 G_0 G0) 是从初始状态 ( $S_0 $) 开始的累计奖励。
- ( γ \gamma γ) 是折扣因子,反映了未来奖励的重要性。
随机型策略定义
随机型策略 ( π ( a ∣ s ) \pi(a|s) π(a∣s) ) 定义了在状态 ( s s s) 下采取动作 ( a a a) 的概率。它允许在同一状态下选择不同的动作,并通过概率的方式平衡不同动作之间的权重。
-
策略表示:
π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a|s) = P(A_t = a \mid S_t = s) π(a∣s)=P(At=a∣St=s)
在无保护左转场景中,可能的动作包括“等待”(例如 ( a 1 a_1 a1))和“尝试左转”(例如 ( a 2 a_2 a2 ))。 -
策略示例:
- 等待( a_1 ): ( π ( a 1 ∣ s ) = 0.7 ) ( \pi(a_1|s) = 0.7 ) (π(a1∣s)=0.7)
- 尝试左转( a 2 a_2 a2):( p i ( a 2 ∣ s ) = 0.3 pi(a_2|s) = 0.3 pi(a2∣s)=0.3 )
-
贝尔曼方程求解过程
使用贝尔曼方程求解涉及到递归计算值函数,并通过策略迭代最终找到最优策略。以下是具体步骤:
a. 状态和值函数定义
- 状态 ( s s s):包括车辆在路口时的位置信息、对向车辆的速度和距离、交通灯状态等。
- 动作 ( a a a):在每个状态下可采取的动作,例如“等待”或“尝试左转”。
- 奖励 ( R ( s , a , s ′ ) R(s,a,s') R(s,a,s′)):即时奖励,例如成功左转会带来正奖励,碰撞则带来负奖励,等待则可能带来小的负奖励。
b. 贝尔曼期望方程用于策略评估
策略评估是指在给定策略 ( π \pi π) 的情况下,计算每个状态的值函数 ( V π ( s ) V^{\pi}(s) Vπ(s))。
- 贝尔曼期望方程:
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ∑ s ′ ∈ S P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V π ( s ′ ) ] V^{\pi}(s) = \sum_{a \in A} \pi(a|s) \sum_{s' \in S} P(s'|s,a) \left[ R(s,a,s') + \gamma V^{\pi}(s') \right] Vπ(s)=a∈A∑π(a∣s)s′∈S∑P(s′∣s,a)[R(s,a,s′)+γVπ(s′)]
其中:- ( P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)) 是从状态 ( s s s) 采取动作 ( a a a) 后转移到状态 ( s ′ s' s′) 的概率。
- ( R ( s , a , s ′ ) R(s,a,s') R(s,a,s′) ) 是从 ( s s s) 到 ( s ′ s' s′) 所获得的即时奖励。
步骤:
- 初始化值函数 ( V π ( s ) V^{\pi}(s) Vπ(s)),通常初始为0或小的随机值。
- 迭代更新值函数,使用贝尔曼期望方程计算每个状态的值函数,直到 ( V π ( s ) V^{\pi}(s) Vπ(s)) 收敛。
c. 贝尔曼最优方程用于策略改进
策略改进是指在策略评估之后,利用状态值函数来更新策略,使得在每个状态下都选择最优动作,即能够带来最大值函数的动作。
- 贝尔曼最优方程:
V ∗ ( s ) = max a ∈ A ∑ s ′ ∈ S P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V ∗ ( s ′ ) ] V^*(s) = \max_{a \in A} \sum_{s' \in S} P(s'|s,a) \left[ R(s,a,s') + \gamma V^*(s') \right] V∗(s)=a∈Amaxs′∈S∑P(s′∣s,a)[R(s,a,s′)+γV∗(s′)]
步骤:
-
策略改进:利用贝尔曼最优方程更新策略 ($ \pi(s) $),以使每个状态下选择最优动作的概率更大。
π ′ ( a ∣ s ) = arg max a ∈ A ∑ s ′ ∈ S P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V π ( s ′ ) ] \pi'(a|s) = \arg\max_{a \in A} \sum_{s' \in S} P(s'|s,a) \left[ R(s,a,s') + \gamma V^{\pi}(s') \right] π′(a∣s)=arga∈Amaxs′∈S∑P(s′∣s,a)[R(s,a,s′)+γVπ(s′)]
-
重复策略评估和策略改进,直到策略 ($ \pi $) 收敛,即策略不再变化。
d. 示例:无保护左转的决策过程
假设我们在无保护左转的场景中使用贝尔曼方程进行求解:
-
状态:
- 当前车辆的位置和速度。
- 对向车辆的速度和距离。
- 环境信息,如是否有其他车辆在进行左转。
-
动作:
- ( a_1 ):等待。
- ( a_2 ):尝试左转。
-
奖励:
- 成功左转 ( R ( s , a 2 , s ′ ) = + 10 R(s,a_2,s') = +10 R(s,a2,s′)=+10)。
- 发生碰撞 ( R ( s , a 2 , s ′ ) = − 100 R(s,a_2,s') = -100 R(s,a2,s′)=−100 )。
- 等待 ( R ( s , a 1 , s ′ ) = − 1 R(s,a_1,s') = -1 R(s,a1,s′)=−1)(消耗时间)。
-
贝尔曼期望方程求解:
- 初始状态值函数设为 0 0 0。
- 根据贝尔曼期望方程,反复计算每个状态下的值函数,评估当前策略的表现。
-
策略改进:
- 根据贝尔曼最优方程调整策略,增加选择成功左转的动作概率,减少选择等待的概率(假设在特定情况下,左转是安全的)。
- 迭代:
- 重复策略评估和策略改进,直到值函数和策略收敛。
-
简单代码实现
此代码实现了状态表示、动作空间的扩展,并通过贝尔曼方程进行策略评估和改进。
- 导入必要的库并定义常量
#include <iostream>
#include <vector>
#include <map>
#include <cmath>
#include <algorithm>
#include <tuple>
#include <limits>const double GAMMA = 0.9; // 折扣因子
const double THRESHOLD = 1e-6; // 策略评估中的收敛阈值
- 定义状态和动作
// 定义动作类型
enum Action { WAIT, // 等待ACCELERATE_WAIT, // 加速等待DECELERATE_WAIT, // 减速等待TURN_LEFT, // 左转ACCELERATE_TURN_LEFT,// 加速左转DECELERATE_TURN_LEFT // 减速左转
};// 定义状态结构体
struct State {double car_position; // 车辆到十字路口的距离double car_speed; // 当前车辆的速度double oncoming_car_position; // 对面来车到路口的距离double oncoming_car_speed; // 对面来车的速度// 重载 < 运算符以用于在 map 中作为 keybool operator<(const State& other) const {return std::tie(car_position, car_speed, oncoming_car_position, oncoming_car_speed) <std::tie(other.car_position, other.car_speed, other.oncoming_car_position, other.oncoming_car_speed);}
};
- 定义策略和奖励函数
// 策略结构体,包含每个状态下动作的概率分布
struct Policy {std::map<State, std::map<Action, double>> actionProbabilities;double getProbability(const State& s, Action a) const {return actionProbabilities.at(s).at(a);}void setProbability(const State& s, Action a, double prob) {actionProbabilities[s][a] = prob;}
};// 奖励函数定义
double getReward(const State& s, Action a, const State& s_prime) {// 根据不同的状态和动作对奖励函数进行设定if (a == TURN_LEFT && s_prime.car_position == 0 && s_prime.oncoming_car_position > 5) return 10; // 成功左转if (a == TURN_LEFT && s_prime.car_position == 0 && s_prime.oncoming_car_position <= 5) return -100; // 发生碰撞if (a == WAIT) return -1; // 等待if (a == ACCELERATE_WAIT || a == DECELERATE_WAIT) return -0.5; // 等待时加速/减速,略有惩罚return 0;
}
- 定义状态转移概率
// 状态转移函数定义
double getTransitionProbability(const State& s, Action a, const State& s_prime) {// 根据动作定义不同的状态转移概率if (a == TURN_LEFT) {if (s_prime.car_position == 0 && s_prime.oncoming_car_position > 5) return 0.8; // 成功左转的概率if (s_prime.car_position == 0 && s_prime.oncoming_car_position <= 5) return 0.2; // 发生碰撞的概率}if (a == WAIT) {if (s_prime.car_position == s.car_position - s.car_speed) return 1.0; // 继续等待}// 加速/减速等待的状态转移概率if (a == ACCELERATE_WAIT) {if (s_prime.car_speed == s.car_speed + 1) return 1.0;}if (a == DECELERATE_WAIT) {if (s_prime.car_speed == s.car_speed - 1) return 1.0;}// 加速/减速左转的状态转移概率if (a == ACCELERATE_TURN_LEFT || a == DECELERATE_TURN_LEFT) {// 这里可以进一步细化转移概率}return 0.0;
}
- 贝尔曼方程的实现
void policyEvaluation(const std::vector<State>& states, Policy& policy, std::map<State, double>& V) {double delta;do {delta = 0;for (const State& s : states) {double v = V[s];double newValue = 0.0;for (Action a : {WAIT, ACCELERATE_WAIT, DECELERATE_WAIT, TURN_LEFT, ACCELERATE_TURN_LEFT, DECELERATE_TURN_LEFT}) {double actionValue = 0.0;for (const State& s_prime : states) {double prob = getTransitionProbability(s, a, s_prime);actionValue += prob * (getReward(s, a, s_prime) + GAMMA * V[s_prime]);}newValue += policy.getProbability(s, a) * actionValue;}V[s] = newValue;delta = std::max(delta, std::fabs(v - V[s]));}} while (delta > THRESHOLD); // 迭代直到值函数收敛
}void policyImprovement(const std::vector<State>& states, Policy& policy, const std::map<State, double>& V) {bool policyStable = true;for (const State& s : states) {Action bestAction;double bestActionValue = -std::numeric_limits<double>::infinity();for (Action a : {WAIT, ACCELERATE_WAIT, DECELERATE_WAIT, TURN_LEFT, ACCELERATE_TURN_LEFT, DECELERATE_TURN_LEFT}) {double actionValue = 0.0;for (const State& s_prime : states) {double prob = getTransitionProbability(s, a, s_prime);actionValue += prob * (getReward(s, a, s_prime) + GAMMA * V.at(s_prime));}if (actionValue > bestActionValue) {bestActionValue = actionValue;bestAction = a;}}// 更新策略if (policy.getProbability(s, bestAction) != 1.0) {policyStable = false;}policy.setProbability(s, bestAction, 1.0);for (Action a : {WAIT, ACCELERATE_WAIT, DECELERATE_WAIT, TURN_LEFT, ACCELERATE_TURN_LEFT, DECELERATE_TURN_LEFT}) {if (a != bestAction) {policy.setProbability(s, a, 0.0);}}}if (policyStable) {std::cout << "Policy is stable." << std::endl;}
}
- 策略迭代的完整过程
void policyIteration(std::vector<State>& states, Policy& policy) {std::map<State, double> V;for (const State& s : states) {V[s] = 0.0; // 初始化值函数}bool policyStable = false;while (!policyStable) {policyEvaluation(states, policy, V); // 策略评估policyImprovement(states, policy, V); // 策略改进}
}int main() {// 定义状态集,假设有几个离散状态State s0 = {10, 1, 15, 1}; // 初始状态,车与路口距离10米,速度1 m/s,对面车距路口15米State s1 = {0, 0, 0, 0}; // 左转成功状态State s2 = {5, 1, 5, 1}; // 危险状态,车距路口5米,对面车也距路口5米std::vector<State> states = {s0, s1, s2};// 初始化策略,假设初始时每个动作均等概率Policy policy;for (const State& s : states) {policy.setProbability(s, WAIT, 1.0 / 6);policy.setProbability(s, ACCELERATE_WAIT, 1.0 / 6);policy.setProbability(s, DECELERATE_WAIT, 1.0 / 6);policy.setProbability(s, TURN_LEFT, 1.0 / 6);policy.setProbability(s, ACCELERATE_TURN_LEFT, 1.0 / 6);policy.setProbability(s, DECELERATE_TURN_LEFT, 1.0 / 6);}// 执行策略迭代policyIteration(states, policy);// 输出最终的策略for (const auto& pair : policy.actionProbabilities) {const State& s = pair.first;std::cout << "State: (pos=" << s.car_position << ", speed=" << s.car_speed << ", oncoming_pos=" << s.oncoming_car_position << ", oncoming_speed=" << s.oncoming_car_speed << ")\n";for (const auto& action_prob : pair.second) {std::cout << " Action: " << action_prob.first << " -> Prob: " << action_prob.second << std::endl;}}return 0;
}
- 代码解析
- 状态与动作表示:使用了结构体
State表示状态,Action表示动作。状态包含了车辆与对面车辆的位置信息和速度信息。 - 策略表示:使用
Policy结构体来表示策略,每个状态下的动作有相应的概率。 - 贝尔曼方程实现:通过
policyEvaluation函数实现值函数的迭代更新,并使用policyImprovement函数进行策略改进。 - 策略迭代:在
policyIteration函数中,循环进行策略评估和策略改进,直到策略稳定。
- 运行说明
在该代码中,假设我们只有三个离散状态和一套初始策略,通过策略迭代最终会得出一个收敛的最优策略。你可以根据实际需求增加状态集和定义更精细的状态转移概率及奖励函数。
2.2 价值迭代与策略迭代
2.2.1 价值迭代

价值迭代(Value Iteration)的解释
价值迭代是一种动态规划算法,用于求解马尔可夫决策过程(MDP)的最优策略。与策略迭代不同,价值迭代直接通过更新值函数来逼近最优值函数,并从中导出最优策略。它不需要在每个迭代步骤中显式地评估和改进策略,而是通过贝尔曼最优方程的迭代来收敛到最优值函数。
贝尔曼最优方程
贝尔曼最优方程定义了最优值函数 ( V ∗ ( s ) V^*(s) V∗(s)) 的递推关系:
V ∗ ( s ) = max a ∑ s ′ P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V ∗ ( s ′ ) ] V^*(s) = \max_{a} \sum_{s'} P(s'|s,a) \left[ R(s,a,s') + \gamma V^*(s') \right] V∗(s)=amaxs′∑P(s′∣s,a)[R(s,a,s′)+γV∗(s′)]
其中:
- ( V ∗ ( s ) V^*(s) V∗(s)) 是状态 ( s s s) 的最优值函数。
- ( a a a) 是在状态 ( s s s) 下可采取的动作。
- ( P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)) 是从状态 ( s s s) 经过动作 ( a a a) 转移到状态 ( s ′ s' s′) 的概率。
- ( R ( s , a , s ′ ) R(s,a,s') R(s,a,s′)) 是采取动作 ( a a a) 后从状态 ( s s s ) 转移到状态 ( s ′ s' s′) 所获得的即时奖励。
- ( γ \gamma γ) 是折扣因子,控制未来奖励的重要性。
价值迭代的过程
价值迭代的核心是将贝尔曼最优方程转化为一种更新规则,直接对值函数进行迭代计算,直到收敛为止。具体步骤如下:
-
初始化:为每个状态 ( s s s ) 设定初始值 ( V ( s ) V(s) V(s)),通常可以设置为 0 或一个任意值。
-
值函数更新:对于每个状态 ( s s s ),更新其值函数 ( V ( s ) V(s) V(s) ):
V ( s ) ← max a ∑ s ′ P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V ( s ′ ) ] V(s) \leftarrow \max_{a} \sum_{s'} P(s'|s,a) \left[ R(s,a,s') + \gamma V(s') \right] V(s)←amaxs′∑P(s′∣s,a)[R(s,a,s′)+γV(s′)] -
收敛检查:重复步骤 2,直到 ($ V(s) $) 的变化在所有状态 ( $s $) 上都小于预定的阈值(如 ( $\epsilon $)),即认为值函数已收敛。
-
提取策略:当值函数 ( V ( s ) V(s) V(s)) 收敛后,可以根据最优值函数从每个状态 ( s s s) 选择最优动作 ( a ∗ a^* a∗):
π ∗ ( s ) = arg max a ∑ s ′ P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V ( s ′ ) ] \pi^*(s) = \arg\max_{a} \sum_{s'} P(s'|s,a) \left[ R(s,a,s') + \gamma V(s') \right] π∗(s)=argamaxs′∑P(s′∣s,a)[R(s,a,s′)+γV(s′)]价值迭代将贝尔曼最优方程转为更新规则
价值迭代的关键在于将贝尔曼最优方程转化为一种迭代更新规则。具体来说,价值迭代通过反复应用贝尔曼最优方程的右侧部分来更新值函数。每次迭代中,值函数 ( V ( s ) V(s) V(s)) 在每个状态下都被更新为其当前值和未来预期奖励的最大可能值。通过这种迭代,值函数逐渐逼近最优值函数 ( V ∗ ( s ) V^*(s) V∗(s))。
这一过程可以看作是“修正”当前值函数,使其更接近最优值函数。当值函数不再发生显著变化时,价值迭代收敛到最优解,从而得到最优策略。
价值迭代的伪代码
通过反复更新值函数来逼近最优值函数,并从中提取最优策略。
输入:S: 状态空间A: 动作空间P(s'|s,a): 状态转移概率函数R(s,a,s'): 奖励函数γ: 折扣因子 (0 ≤ γ < 1)θ: 收敛阈值 (一个很小的正数)输出:V: 状态值函数,V(s) 是状态 s 的最优值π*: 最优策略初始化:对于所有 s ∈ S, V(s) ← 0重复执行 (迭代):Δ ← 0对于每个状态 s ∈ S:v ← V(s) // 存储当前状态 s 的旧值V(s) ← max_a Σ_s' P(s'|s,a) * [R(s,a,s') + γ * V(s')] // 更新值函数Δ ← max(Δ, |v - V(s)|) // 记录值函数的最大变化量如果 Δ < θ, 则退出循环 (值函数已收敛)提取策略:对于每个状态 s ∈ S:π*(s) ← argmax_a Σ_s' P(s'|s,a) * [R(s,a,s') + γ * V(s')] // 提取最优策略返回:V, π* // 返回最终的最优值函数和最优策略
伪代码说明
-
初始化:
- 将所有状态的值函数 ( V(s) ) 初始化为 0 或者任意一个初始值。
-
主循环:
- 通过一个重复执行的循环逐步更新每个状态的值函数 ( V(s) )。
- 在每次迭代中,对于每个状态 ( s ),计算可能采取的所有动作的期望值,并将当前状态的值函数更新为这些期望值的最大值。
- 记录值函数变化的最大差异 ( Δ ),如果这个差异小于阈值 ( θ ),则认为值函数已经收敛,停止迭代。
-
策略提取:
- 在值函数收敛后,针对每个状态 ( s ),选择使期望值最大的动作作为最优策略 ( π ∗ ( s ) π^*(s) π∗(s))。
-
返回:
- 返回最终的最优值函数 ( V ) 和最优策略 ( π ∗ ( s ) π^*(s) π∗(s))。
价值迭代的核心
伪代码展示了价值迭代的两个关键部分:值函数更新和策略提取。值函数更新是通过贝尔曼最优方程的递归形式来实现的,而策略提取则基于已经收敛的值函数来选择最优动作。

主要的难点和瓶颈
在自动驾驶中,使用马尔可夫决策过程(MDP)和价值迭代方法来解决决策问题,尤其是像无保护左转这样复杂的交通场景时,存在几个主要的难点和瓶颈:
-
状态空间的复杂性和维度问题
- 难点:无保护左转场景涉及大量的变量,如自车的速度和位置、对向车辆的速度和位置、交通信号状态、行人等。每个变量都增加了状态空间的维度,使得状态空间呈指数增长。这种联合状态空间使得枚举和计算每个状态变得不切实际,遍历 s,嵌套遍历action。
- 瓶颈:需要离散化状态空间,但这会损失精度。更为复杂的连续状态空间则需要函数逼近方法,如深度强化学习,这增加了计算复杂性。
-
实时性要求
- 难点:自动驾驶系统必须实时处理复杂的决策问题,尤其是在动态、不可预测的环境下。无保护左转涉及快速变化的交通状况,算法必须在极短的时间内做出准确的决策。
- 瓶颈:价值迭代等方法通常需要多次迭代才能收敛,难以满足实时决策的要求。在实际应用中,可能需要使用近似算法或剪枝技术来减少计算量。
-
不确定性处理
- 难点:交通环境充满不确定性,其他车辆的行为无法完全预测。无保护左转过程中,系统需要处理对面来车的不确定性,以及潜在的突发情况(如行人突然出现)。
- 瓶颈:MDP 假设状态转移概率已知,但在实际应用中,精确地建模这些概率很困难。系统可能需要实时学习和更新这些概率分布,或依赖于历史数据的统计分析,但这在动态场景中具有挑战性。
-
复杂的奖励函数设计
- 难点:无保护左转需要平衡多个目标,如安全性、效率、舒适性等。这些目标可能是相互冲突的。例如,过度关注安全可能会导致过于保守的决策,从而影响驾驶效率。
- 瓶颈:设计合理的奖励函数来平衡这些目标十分困难。奖励函数的细微变化可能导致完全不同的行为策略。找到适合所有情境的通用奖励函数几乎不可能,必须针对不同的场景进行调试和优化。
2.2.2 价值迭代举例
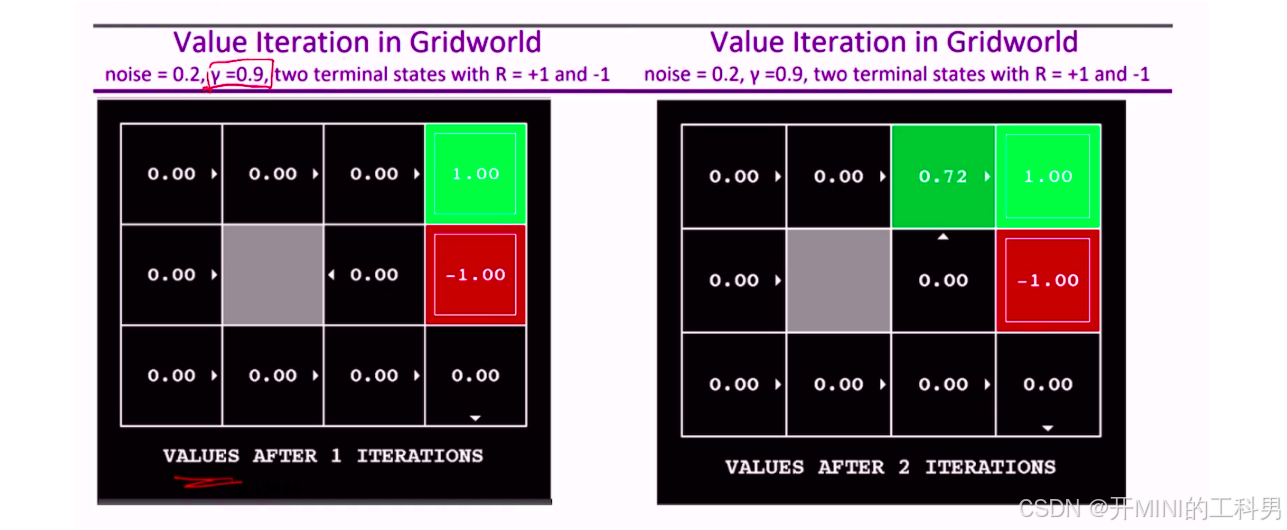
Gridworld说明
网格世界(Gridworld)是强化学习中的经典环境,用于演示如何通过价值迭代、策略迭代等方法来求解马尔科夫决策过程(MDP)。它的含义和用途如下:
a.网格世界的定义
- 环境:网格世界通常是一个二维的网格,每个格子代表一个状态。
- 状态:每个格子都可以视为一个状态(state),通常用 (x, y) 坐标来表示。
- 动作:在每个状态,智能体(Agent)可以执行一组动作(例如:上、下、左、右移动,也有可能会移动失败,停留在原地),使它从一个状态转移到另一个状态。
- 转移概率:动作通常具有一定的不确定性,即执行某个动作可能不会100%导致预期的结果。可能会有噪声导致智能体移动到不同的状态。
- 奖励:某些状态可能带有奖励(如 +1,-1),表示在到达这些状态时智能体获得的即时奖励。
b.网格世界的具体含义
-
状态:图中的每一个方块代表一个状态。比如左上角的状态,右下角的状态等。
-
终端状态(Terminal State):
- 绿色方块(+1):达到这个状态表示任务成功,获得 +1 奖励。
- 红色方块(-1):达到这个状态表示任务失败,获得 -1 惩罚。
- 一旦智能体进入终端状态,它将无法再进行进一步的移动。
-
动作和转移概率:
- 智能体在网格中的每个状态都可以选择向上、向下、向左、向右移动。
- 执行动作时,由于存在噪声(图中的噪声参数为 0.2),实际的移动可能不会按照预期进行。例如,如果选择向上移动,有 0.8 的概率真的向上移动,但有 0.1 的概率会向左或向右移动。
-
价值迭代的过程:
- 初始化:一开始,所有非终端状态的值 ( V(s) ) 都初始化为 0。
- 迭代:通过价值迭代算法,逐步更新每个状态的值。这种更新基于贝尔曼方程,用以估计在该状态下采取最佳策略时的预期长期回报。
- 收敛:随着多次迭代,状态的值会逐渐收敛到一个稳定的值,即最优值函数。此时可以通过最大化这个值来得出最优策略。
迭代过程

贝尔曼方程描述了一个状态的值(价值)如何基于该状态下采取的动作和随后的状态值来更新。一般形式为:
V ( s ) = max a ∑ s ′ P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ ⋅ V ( s ′ ) ] V(s) = \max_a \sum_{s'} P(s' | s, a) \left[ R(s, a, s') + \gamma \cdot V(s') \right] V(s)=amaxs′∑P(s′∣s,a)[R(s,a,s′)+γ⋅V(s′)]
具体计算
噪声 noise = 0.2,折扣因子 γ = 0.9,并且有两个终止状态,其中一个的回报是 +1(绿色),另一个的回报是 -1(红色)。
迭代1次后的结果
在图的左侧,所有非终止状态的初始价值为 0。两个终止状态的价值分别为 1.00 和 -1.00。第1次迭代结束后,所有非终止状态的价值仍然为 0.00,这是因为这是第一次迭代,状态的价值更新还没有传播到周围的状态。
迭代2次后的结果
在第2次迭代之后,非终止状态的价值开始更新。对于第一行第三列的状态( V ( 1 , 3 ) = 0.72 V(1, 3) = 0.72 V(1,3)=0.72)。
为了计算出该状态的价值,我们需要考虑所有可能的行动及其对应的回报。
-
向右移动:
- 直接进入终止状态 +1, 所以回报为 ( γ × 1.00 = 0.9 × 1.00 = 0.9 \gamma \times 1.00 = 0.9 \times 1.00 = 0.9 γ×1.00=0.9×1.00=0.9 )
- 由于噪声 0.2,有一定概率移动失败,可能上下移动,这些方向的回报仍然是 0。
因此总期望回报为:
0.8 × 0.9 + 0.2 × 0 = 0.72 0.8 \times 0.9 + 0.2 \times 0 = 0.72 0.8×0.9+0.2×0=0.72
所以,这个状态的价值在第二次迭代时为 0.72。

迭代3次后的结果
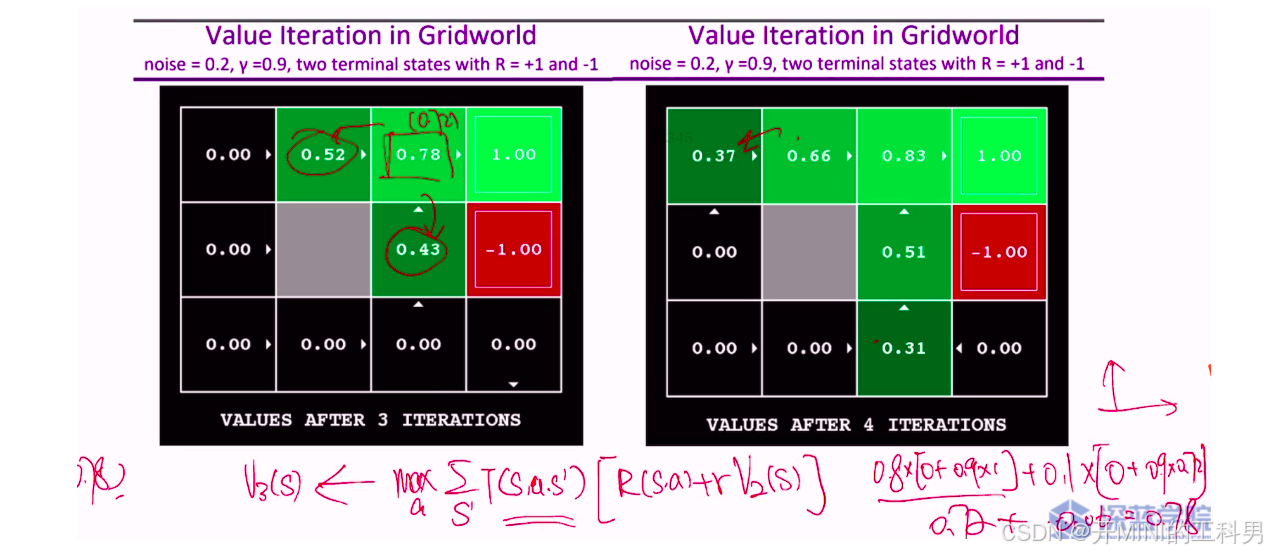
第一行第三列的值计算( V ( 1 , 3 ) = 0.78 V(1, 3) = 0.78 V(1,3)=0.78)
-
向右移动: 0.8 × ( 0 + 0.9 × 1 ) = 0.72 0.8 \times (0 + 0.9 \times 1) = 0.72 0.8×(0+0.9×1)=0.72
-
20%概率向下或向下移动:
往下移动:reward 为0
往上走,仍有10%的一定概率留在原地,且留在原地的reward 为0.72 : 0.1 × ( 0 + 0.9 × 0.72 ) = 0.06 0.1\times (0 + 0.9 \times 0.72) = 0.06 0.1×(0+0.9×0.72)=0.06
向右移动的总期望值为: 0.72 + 0.06 = 0.78 0.72 + 0.06 = 0.78 0.72+0.06=0.78
第二行第三列的值计算( V ( 2 , 3 ) = 0.43 V(2, 3) = 0.43 V(2,3)=0.43)
对于这一状态,主要有以下几个可能的移动方向:
1. 向右移动
- 移动到终止状态 -1.00:
0.8 × ( − 1.00 ) = − 0.8 0.8 \times (-1.00) = -0.8 0.8×(−1.00)=−0.8 - 移动到上方的状态 0.72:
0.1 × 0.72 × γ = 0.1 × 0.72 × 0.9 = 0.0648 0.1 \times 0.72 \times \gamma = 0.1 \times 0.72 \times 0.9 = 0.0648 0.1×0.72×γ=0.1×0.72×0.9=0.0648 - 移动到下方的状态 0.00:
0.1 × 0.00 = 0 0.1 \times 0.00 = 0 0.1×0.00=0
向右移动的期望值为:
− 0.8 + 0.0648 + 0 = − 0.7352 -0.8 + 0.0648 + 0 = -0.7352 −0.8+0.0648+0=−0.7352
2. 向上移动
- 移动到上方的状态 0.72:
0.8 × 0.72 × γ = 0.8 × 0.72 × 0.9 = 0.5184 0.8 \times 0.72 \times \gamma = 0.8 \times 0.72 \times 0.9 = 0.5184 0.8×0.72×γ=0.8×0.72×0.9=0.5184 - 移动到左侧的状态(灰色障碍)或右侧终止状态:
0.1 × 0 + 0.1 × ( − 1.00 ) × γ = 0.1 × − 0.9 = − 0.09 0.1 \times 0 + 0.1 \times (-1.00) \times \gamma = 0.1 \times -0.9 = -0.09 0.1×0+0.1×(−1.00)×γ=0.1×−0.9=−0.09
向上移动的期望值为:
0.5184 − 0.09 = 0.4284 0.5184 - 0.09 = 0.4284 0.5184−0.09=0.4284
3. 向左移动
- 移动到灰色障碍的状态(价值为0):
0.8 × 0 = 0 0.8 \times 0 = 0 0.8×0=0 - 移动到上方的状态 0.72:
0.1 × 0.72 × γ = 0.1 × 0.72 × 0.9 = 0.0648 0.1 \times 0.72 \times \gamma = 0.1 \times 0.72 \times 0.9 = 0.0648 0.1×0.72×γ=0.1×0.72×0.9=0.0648 - 移动到下方的状态 0.00:
0.1 × 0.00 = 0 0.1 \times 0.00 = 0 0.1×0.00=0
向左移动的期望值为:
0 + 0.0648 + 0 = 0.0648 0 + 0.0648 + 0 = 0.0648 0+0.0648+0=0.0648
4. 向下移动
- 移动到下方的状态 0.00:
0.8 × 0.00 = 0 0.8 \times 0.00 = 0 0.8×0.00=0 - 移动到左侧的状态(灰色障碍)或右侧终止状态:
0.1 × 0 + 0.1 × ( − 1.00 ) × γ = − 0.09 0.1 \times 0 + 0.1 \times (-1.00) \times \gamma = -0.09 0.1×0+0.1×(−1.00)×γ=−0.09
向下移动的期望值为:
0 − 0.09 = − 0.09 0 - 0.09 = -0.09 0−0.09=−0.09
最终结果
在所有可能的移动中,向上移动有最大的期望值(0.4284),因此第二行第三列 V ( 2 , 3 ) V(2, 3) V(2,3) 状态的值更新为 $ 0.43$。
第一行第二列的值( V ( 1 , 2 ) = 0.52 V(1, 2) = 0.52 V(1,2)=0.52)
对于这一状态,主要有以下几个可能的移动方向:
-
向右移动:
- 80%的概率移动到第一行第三列状态,其价值为
0.72。
- 80%的概率移动到第一行第三列状态,其价值为
-
10%的概率由于噪声,上下移动到第一行第一列或者第二行第二列,这两个位置的初始价值都是
0。因此,向右的期望回报为:
0.8 × 0.72 + 0.1 × 0 + 0.1 × 0 = 0.576 0.8 \times 0.72 + 0.1 \times 0 + 0.1 \times 0 = 0.576 0.8×0.72+0.1×0+0.1×0=0.576
- 向上或向下移动:
- 由于第一行第二列的上方和下方都是边界,因此移动失败,回到原状态,价值依然为
0。
-
向左移动:
- 由于左侧的状态(第一行第一列)初始价值为
0,因此移动到该状态的价值为0。
- 由于左侧的状态(第一行第一列)初始价值为
考虑到 0.9 的折扣因子 γ,选择向右移动的期望价值是:
V ( 1 , 2 ) = γ × 0.576 = 0.9 × 0.576 = 0.5184 ≈ 0.52 V(1, 2) = \gamma \times 0.576 = 0.9 \times 0.576 = 0.5184 \approx 0.52 V(1,2)=γ×0.576=0.9×0.576=0.5184≈0.52
1000次迭代后,趋于稳定
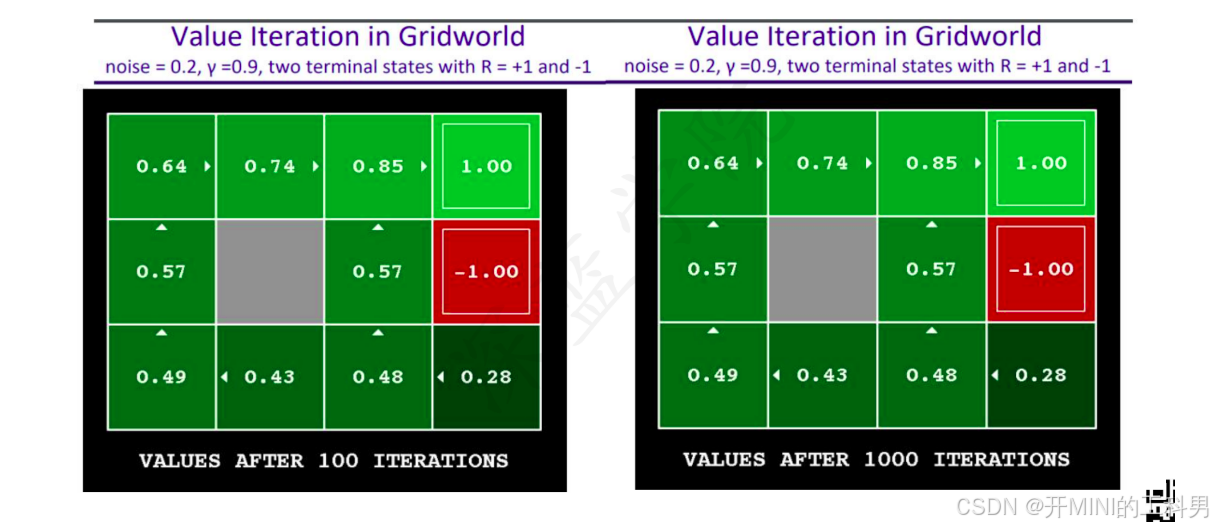
自动驾驶场景举例
对应到自动驾驶场景中,可以理解为不同的驾驶策略和风险管理决策。以下是每种情况的解释:

1. ( γ = 0.1 \gamma = 0.1 γ=0.1), 噪声 = 0.5
场景描述:
自动驾驶系统优先考虑较短期的目标(如到达最近的目的地),并且有较高的不确定性(噪声 = 0.5)。这种情况下,自动驾驶系统可能会选择一条看似较快的路径,但这条路径存在较高的风险(比如拥堵、不确定的道路状况或可能遇到障碍物)。
场景举例:
在城市道路中行驶时,自动驾驶系统选择了一条可能更快但道路状况复杂(如有建筑施工或临时障碍物)的路线。这种决策可能会导致系统在风险较高的情况下行驶。
2. ( γ = 0.99 \gamma = 0.99 γ=0.99), 噪声 = 0
场景描述:
自动驾驶系统优先考虑长期目标(如安全到达更远的目的地),并且道路上几乎没有不确定性(噪声 = 0)。系统会选择最安全、最确定的路径,尽管这条路径可能较长,但保证不会遇到风险。
场景举例:
自动驾驶系统在选择路线时,选择了经过已知没有障碍物和风险的高速公路,尽管这条路线可能比其他路线稍微远一点,但确保了行驶的安全性和可靠性。
3. ( γ = 0.99 \gamma = 0.99 γ=0.99), 噪声 = 0.5
场景描述:
自动驾驶系统考虑长期目标(如到达远方的目标),但同时有一定的道路不确定性(噪声 = 0.5)。系统在这种情况下可能会冒险选择一条更短的路径,尽管这条路径存在一些不确定性或风险。
场景举例:
在长途驾驶时,自动驾驶系统决定通过一条可能有些风险但较快的路线,例如一条在天气状况不稳定的山路上。系统希望通过冒险来节省时间,但仍然考虑了最终的长期目标。
4. ( γ = 0.1 \gamma = 0.1 γ=0.1), 噪声 = 0
场景描述:
自动驾驶系统优先考虑短期目标,并且选择没有任何不确定性或风险的路径(噪声 = 0)。系统在这种情况下会选择最稳妥、最安全的路径,即便这条路径可能较长。
场景举例:
在市区内短距离行驶时,自动驾驶系统选择了一条最安全、没有任何风险的路线,即便这条路线需要绕行,但可以完全避免拥堵或潜在的危险。
总结:
- 高 ( γ \gamma γ) 值:表示系统更注重长期回报(如长途驾驶中的最终目标)。
- 低 ( γ \gamma γ) 值:表示系统更注重短期回报(如市区内的快速到达)。
- 噪声高:表示路径选择过程中存在较大的不确定性和风险。
- 噪声低:表示路径选择过程中几乎没有不确定性,路径更为安全和确定。
2.2.3 策略迭代
基本概念
策略迭代(Policy Iteration)是一种求解马尔可夫决策过程(MDP)的经典算法,它结合了策略评估(Policy Evaluation)和策略改进(Policy Improvement)两个步骤,以便找到最优策略(Optimal Policy)。与价值迭代相比,策略迭代通常收敛更快。
策略迭代的基本步骤
-
策略评估(Policy Evaluation):
- 给定一个策略 ( π \pi π ),计算在该策略下每个状态的价值函数 ( V π ( s ) V^\pi(s) Vπ(s) )。
- 这个过程通过贝尔曼方程反复计算,直到收敛。贝尔曼方程描述了当前状态的价值是基于执行策略后所获得的即时奖励以及未来状态的折扣价值的加权和。
-
策略改进(Policy Improvement):
- 使用当前的价值函数 ( V π ( s ) V^\pi(s) Vπ(s) ) 来更新策略 ( π \pi π )。
- 具体做法是对于每个状态,选择能使得 ( Q ( s , a ) Q(s, a) Q(s,a) ) 最大的动作 ($ a$ ),其中 ( Q ( s , a ) Q(s, a) Q(s,a) ) 是在状态 ($ s$ ) 执行动作 ( a a a ) 后的总价值。这会生成一个新的策略 ( π ′ \pi' π′ )。
-
策略更新:
- 如果新的策略 ( π ′ \pi' π′ ) 与旧的策略 ( π \pi π ) 相同,则算法终止;否则,用 ( π ′ \pi' π′ ) 替换 ( π \pi π ) 并返回第一步,继续进行策略评估。
贝尔曼原理与策略迭代的关系
贝尔曼原理(Bellman Principle)是动态规划的核心思想,它描述了在最优策略下,任意一个状态的最优价值等于当前选择的最优动作所带来的即时奖励加上该动作后进入的状态的折扣价值和。即:
V ∗ ( s ) = max a [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ∗ ( s ′ ) ] V^*(s) = \max_{a} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^*(s') \right] V∗(s)=amax[R(s,a)+γs′∑P(s′∣s,a)V∗(s′)]
在策略迭代中,贝尔曼原理起着至关重要的作用:
-
策略评估:通过贝尔曼方程来计算在当前策略 ( π \pi π ) 下每个状态的价值函数 ( V π ( s ) V^\pi(s) Vπ(s) )。这一过程利用了贝尔曼期望方程:
V π ( s ) = ∑ a π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) ] V^\pi(s) = \sum_{a} \pi(a | s) \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^\pi(s') \right] Vπ(s)=a∑π(a∣s)[R(s,a)+γs′∑P(s′∣s,a)Vπ(s′)]
-
策略改进:通过贝尔曼最优方程来找到最优动作,从而更新策略。这一步的更新规则是选择能够使得 ( Q ( s , a ) Q(s, a) Q(s,a) ) 最大的动作:
π ′ ( s ) = arg max a [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) ] \pi'(s) = \arg\max_{a} \left[ R(s, a) + \gamma \sum_{s'} P(s' | s, a) V^\pi(s') \right] π′(s)=argamax[R(s,a)+γs′∑P(s′∣s,a)Vπ(s′)]



策略迭代举例



3. 参考
《自动驾驶预测与决策技术》
Markov Decision Processes
马尔可夫决策过程原理与代码实现
Part1_自动驾驶决策规划简介
Part2_基于模型的预测方法
Part3_路径与轨迹规划
Part4_时空联合规划
2024.10.11)






:实时时钟)








线程并发)

)
