打卡一道有意义的题。
题签:
通过使用栈可以以非递归方式实现二叉树的中序遍历。
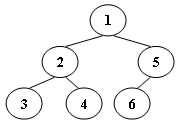
例如,假设遍历一个如下图所示的 66 节点的二叉树(节点编号从 11 到 66)。
则堆栈操作为:push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop()。
我们可以从此操作序列中生成唯一的二叉树。
你的任务是给出这棵树的后序遍历。
输入格式
第一行包含整数 NN,表示树中节点个数。
树中节点编号从 11 到 NN。
接下来 2N2N 行,每行包含一个栈操作,格式为:
Push X,将编号为 XX 的节点压入栈中。Pop,弹出栈顶元素。输出格式
输出这个二叉树的后序遍历序列。
数据保证有解,数和数之间用空格隔开,末尾不能有多余空格。
数据范围
1≤N≤301≤N≤30
输入样例:
6 Push 1 Push 2 Push 3 Pop Pop Push 4 Pop Pop Push 5 Push 6 Pop Pop输出样例:
3 4 2 6 5 1
思路:
一开始没思路,感觉很奇怪,但是看到有人指出非递归遍历的二叉树push过程其实就是先序遍历,pop过程其实就是中序遍历,这么一来那就无脑上板子就好了。
代码:
#include<bits/stdc++.h> using namespace std; const int N=50; int n; int a[N],b[N]; struct tree{int l,r;int v; }p[N]; int cnt,idx; stack<int> stk;int built(int al,int ar,int bl,int br){if(al>ar){return 0;}int r=a[al];int k=0;while(a[al]!=b[k]){k++;}int len=k-bl;p[r].v=r;p[r].l=built(al+1,al+len,bl,bl+len);p[r].r=built(al+len+1,ar,bl+len+1,br);return r; } void print(int x){if(p[x].l){print(p[x].l);}if(p[x].r){print(p[x].r);}cout<<p[x].v<<" ";} int main() {ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=2*n;i++){string str;int x;cin>>str;if(str=="Push"){cin>>x;stk.push(x);a[++cnt]=x;}else{b[++idx]=stk.top();stk.pop();}}built(1,n,1,n);print(a[1]);}

)






舵机+MPU6050陀螺仪模块融合云台模型)









)
