【初阶数据结构】9.二叉树（4）

文章目录

5.二叉树算法题
- 5.1 单值二叉树
- 5.2 相同的树
- 5.3 另一棵树的子树
- 5.4 二叉树遍历
- 5.5 二叉树的构建及遍历
6.二叉树选择题

5.二叉树算法题

5.1 单值二叉树

点击链接做题

代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
typedef struct TreeNode TreeNode;
bool isUnivalTree(struct TreeNode* root) {if(root == NULL){return true;}//root不为空，把root和root->left,root->right比较if(root->left && root->left->val != root->val){return false;}if(root->right && root->right->val != root->val){return false;}//查看左子树和右子树是不是单值二叉树return isUnivalTree(root->left) && isUnivalTree(root->right);
}

5.2 相同的树

点击链接做题

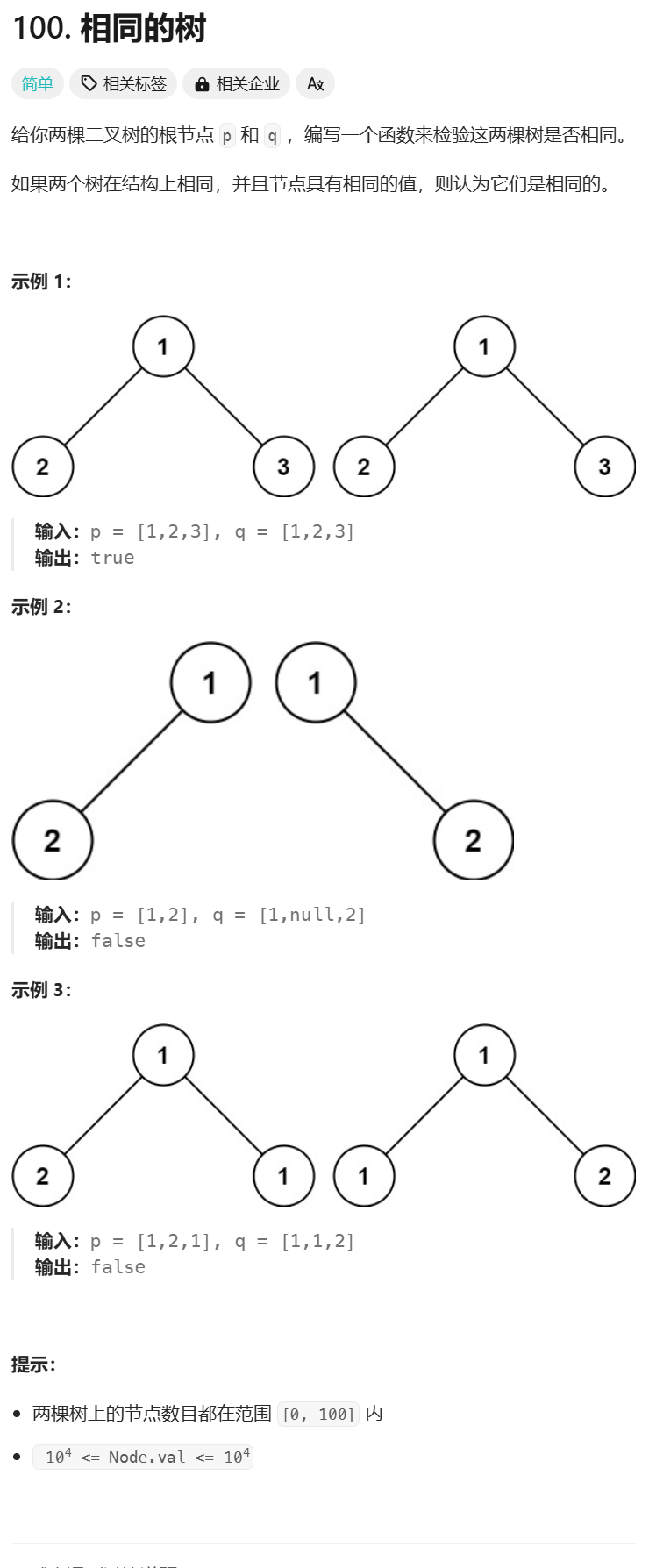
两棵树都为空树------相同的树

其一为空树------不是相同的树

代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
typedef struct TreeNode TreeNode;
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//给了两个树的根节点//判断是否为空树if(p == NULL && q == NULL){return true;}//其一为空if(p == NULL || q == NULL){return false;}//说明都不为空if(p->val != q->val){return false;}//说明结构相同值相同return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

拓展学习

对称二叉树：

点击链接做题

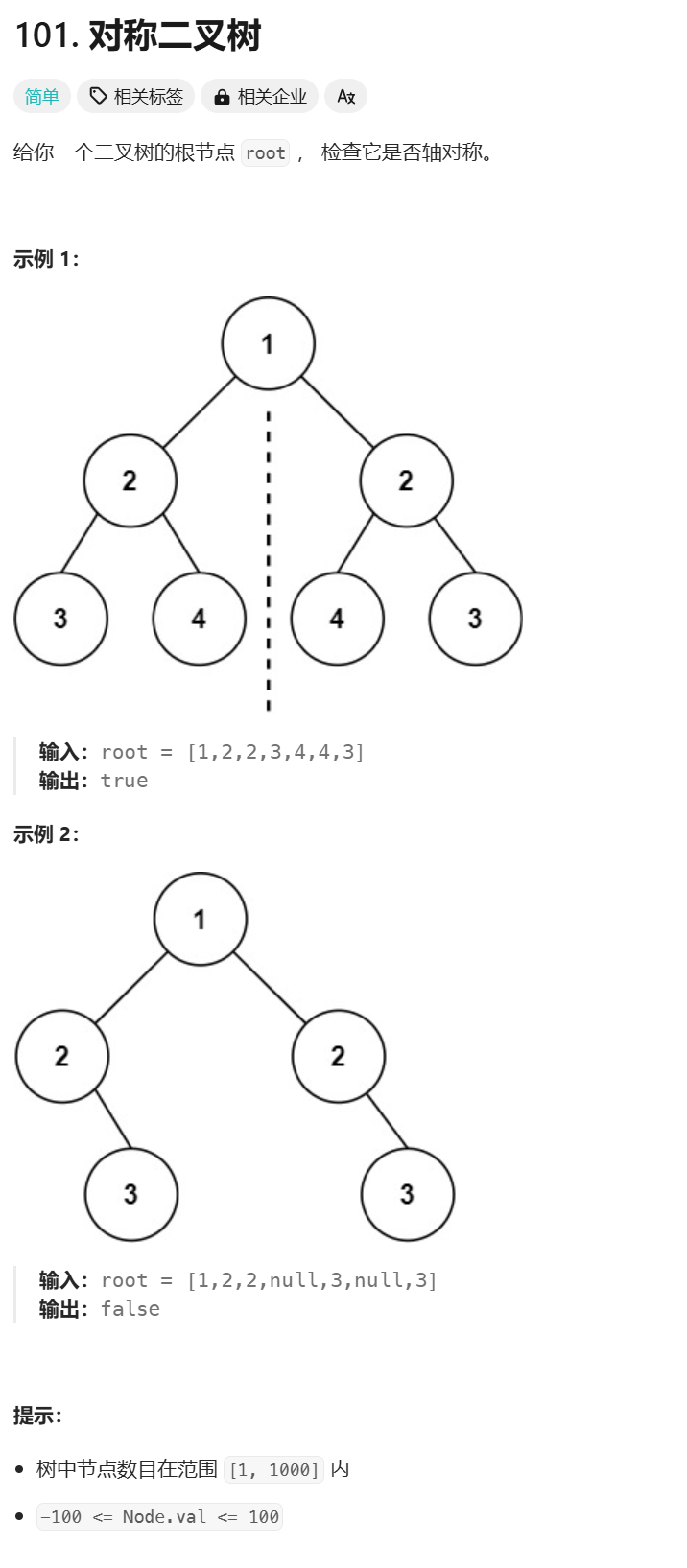
代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
typedef struct TreeNode TreeNode;bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//给了两个树的根节点//判断是否为空树if(p == NULL && q == NULL){return true;}//其一为空if(p == NULL || q == NULL){return false;}//说明都不为空if(p->val != q->val){return false;}//说明结构相同值相同return isSameTree(p->left,q->right) && isSameTree(p->right,q->left);
}bool isSymmetric(struct TreeNode* root) {return isSameTree(root->left,root->right);
}

5.3 另一棵树的子树

点击链接做题

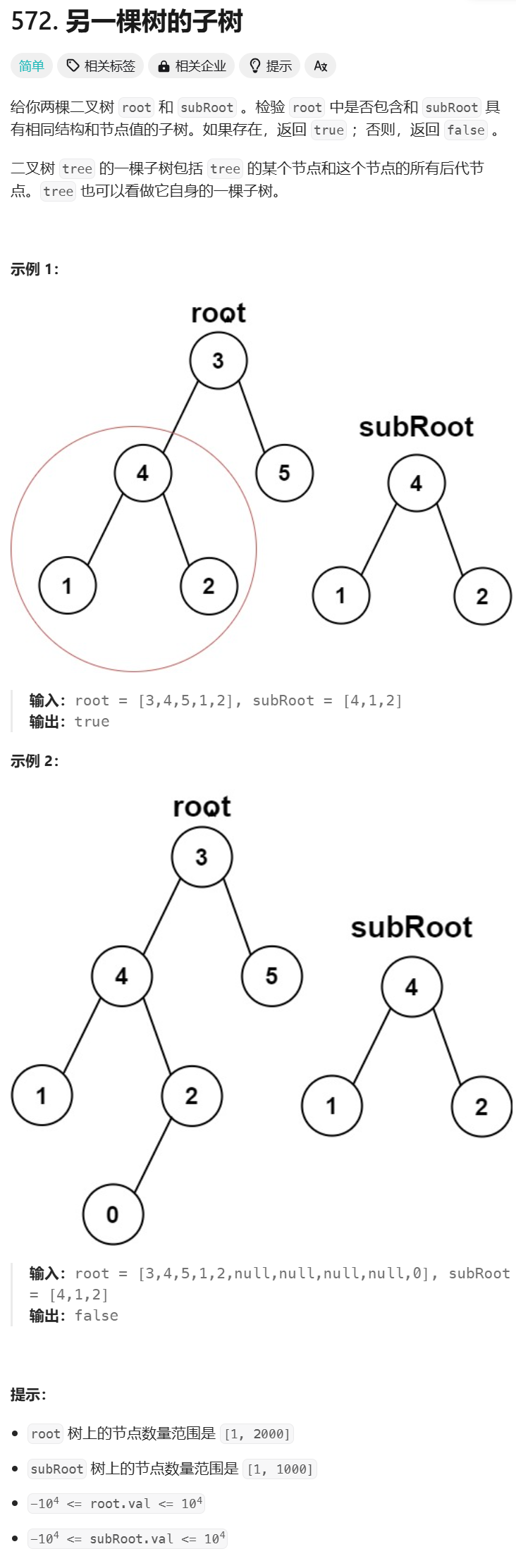
代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
typedef struct TreeNode TreeNode;bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//给了两个树的根节点//判断是否为空树if(p == NULL && q == NULL){return true;}//其一为空if(p == NULL || q == NULL){return false;}//说明都不为空if(p->val != q->val){return false;}//说明结构相同值相同return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}//判断subRoot是不是root的子树
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL){return false;}if(isSameTree(root,subRoot)){return true;}//判断root的左右子树是否和subRoot一样return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

5.4 二叉树遍历

前序遍历：

点击链接做题

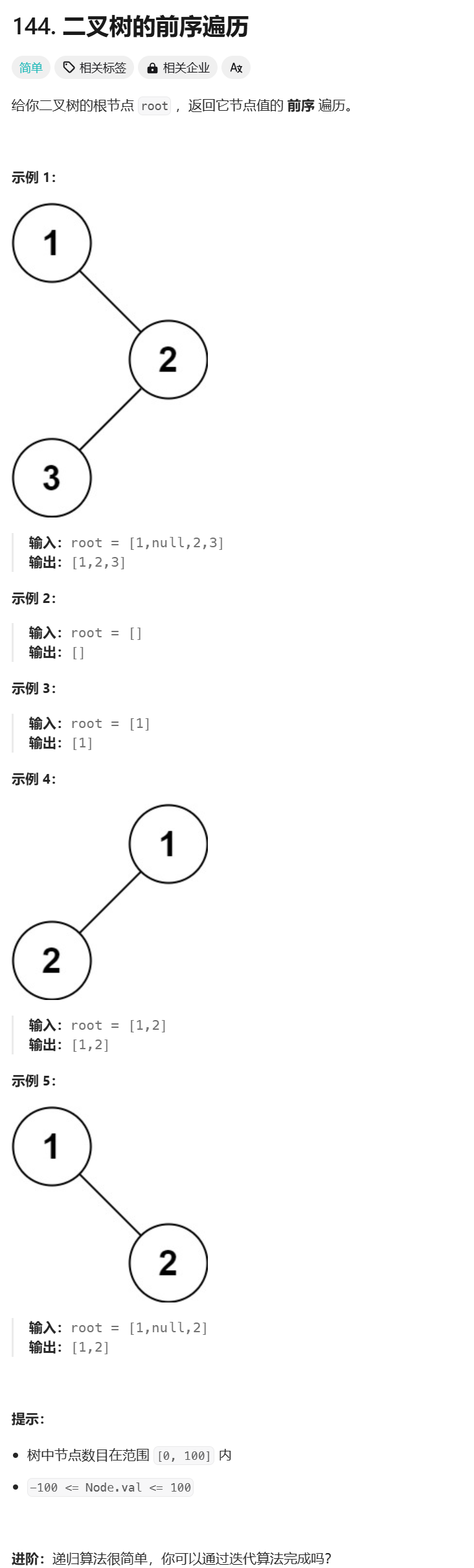
代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
typedef struct TreeNode TreeNode;// ⼆叉树结点个数
int BinaryTreeSize(TreeNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}//表示是当前函数的子函数
void _preorderTraversal(TreeNode* root,int* arr,int* pi){if (root == NULL){return;}//根左右arr[(*pi)++] = root->val;_preorderTraversal(root->left,arr,pi);_preorderTraversal(root->right,arr,pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize) {//int* returnSize是一个整型数组//1.先求出二叉树结点的个数*returnSize = BinaryTreeSize(root);//2.动态申请内容---arr的大小int* returnArr = (int*)malloc(sizeof(int)*(*returnSize));//开始前序遍历int i = 0;_preorderTraversal(root,returnArr,&i);return returnArr;
}

中序遍历：

点击链接做题

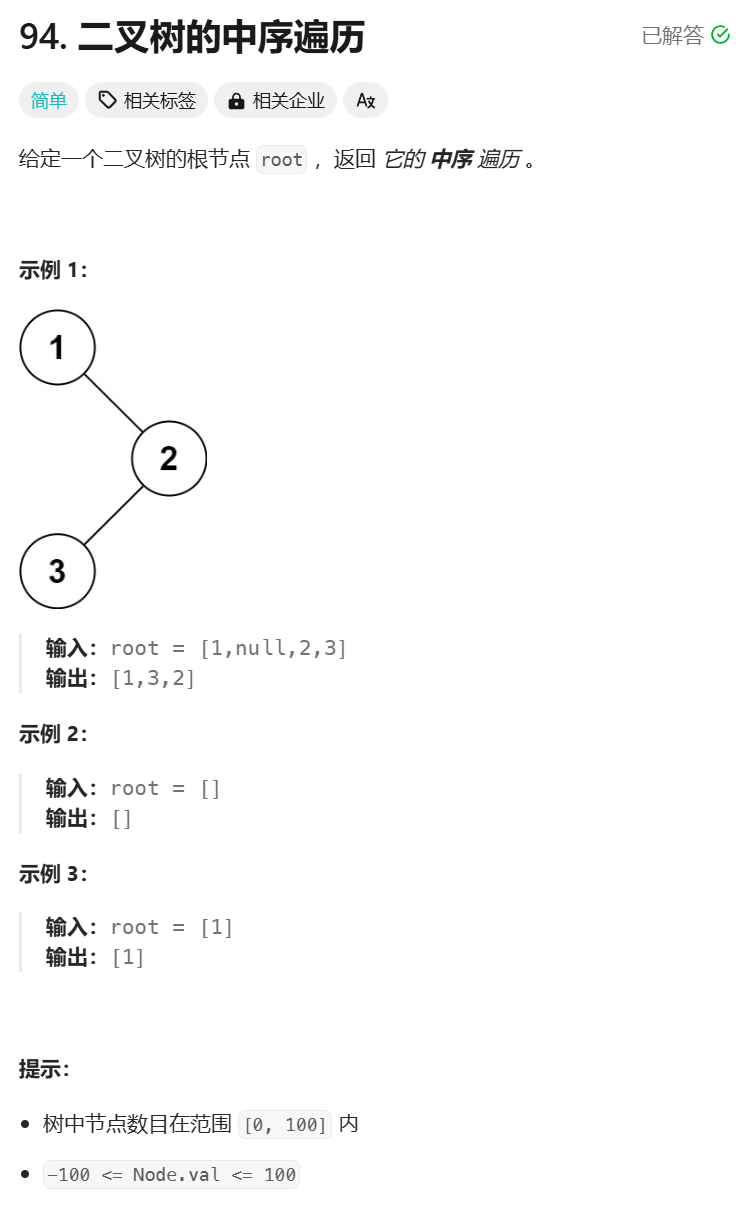
代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/typedef struct TreeNode TreeNode;// ⼆叉树结点个数
int BinaryTreeSize(TreeNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}//表示是当前函数的子函数
void _preorderTraversal(TreeNode* root,int* arr,int* pi){if (root == NULL){return;}//左根右_preorderTraversal(root->left,arr,pi);arr[(*pi)++] = root->val;_preorderTraversal(root->right,arr,pi);
}int* inorderTraversal(struct TreeNode* root, int* returnSize) {//int* returnSize是一个整型数组//1.先求出二叉树结点的个数*returnSize = BinaryTreeSize(root);//2.动态申请内容---arr的大小int* returnArr = (int*)malloc(sizeof(int)*(*returnSize));//开始中序遍历int i = 0;_preorderTraversal(root,returnArr,&i);return returnArr;
}

后序遍历：

点击链接做题

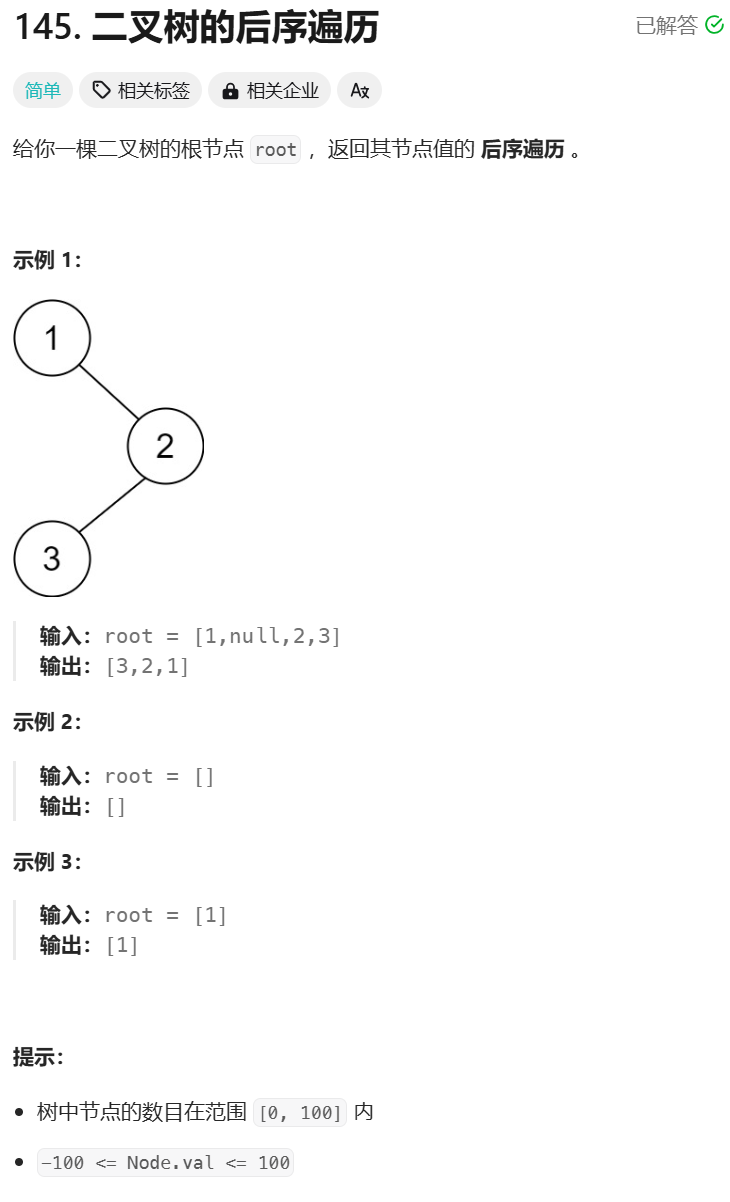
代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
typedef struct TreeNode TreeNode;// ⼆叉树结点个数
int BinaryTreeSize(TreeNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}//表示是当前函数的子函数
void _preorderTraversal(TreeNode* root,int* arr,int* pi){if (root == NULL){return;}//左右根_preorderTraversal(root->left,arr,pi);_preorderTraversal(root->right,arr,pi);arr[(*pi)++] = root->val;
}int* postorderTraversal(struct TreeNode* root, int* returnSize) {//int* returnSize是一个整型数组//1.先求出二叉树结点的个数*returnSize = BinaryTreeSize(root);//2.动态申请内容---arr的大小int* returnArr = (int*)malloc(sizeof(int)*(*returnSize));//开始后序遍历int i = 0;_preorderTraversal(root,returnArr,&i);return returnArr;
}

5.5 二叉树的构建及遍历

点击链接做题

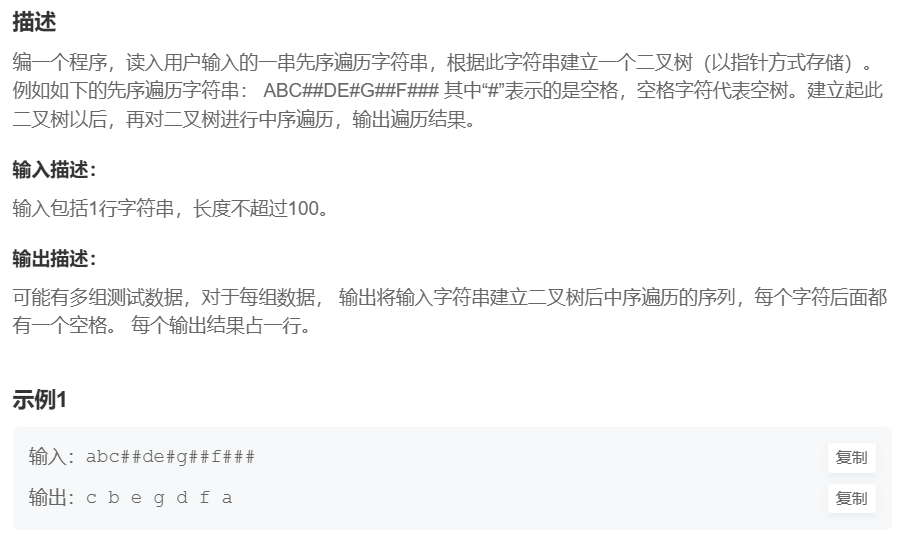
代码：

#include <stdio.h>
typedef struct BinaryTreeNode {char data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;//创建节点
BTNode* buyNode(char x) {BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL) {perror("malloc fail!");exit(1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}//前序遍历
BTNode* creatrTree(char* arr, int* pi) {if (arr[*pi] == '#') {//如果取到的是空字符，那么就不要创建它的根节点(*pi)++;//继续往后走return NULL;}//先创建arr[*pi]这个根节点，然后后置++，这样就到了后面的结点BTNode* root = buyNode(arr[(*pi)++]);root->left = creatrTree(arr, pi);//把根节点的左孩子当作新的根节点root->right = creatrTree(arr, pi);return root;
}//中序遍历--左根右
void InOrder(BTNode* root) {if (root == NULL) {return;}InOrder(root->left);//左printf("%c ", root->data);//中InOrder(root->right);//右
}int main() {//读取用户输入的字符串保存在字符数组中char arr[100];scanf("%s",arr);//根据字符串（前序遍历）创建二叉树int i = 0;BTNode* root = creatrTree(arr, &i);//root指向二叉树的根节点//输出二叉树的中序遍历InOrder(root);return 0;
}

6.二叉树选择题

二叉树性质

对任何一棵二叉树, 如果度为 0 其叶结点个数为n₀ , 度为 2 的分支结点个数为n₂ ,则有n₀=n₂+1

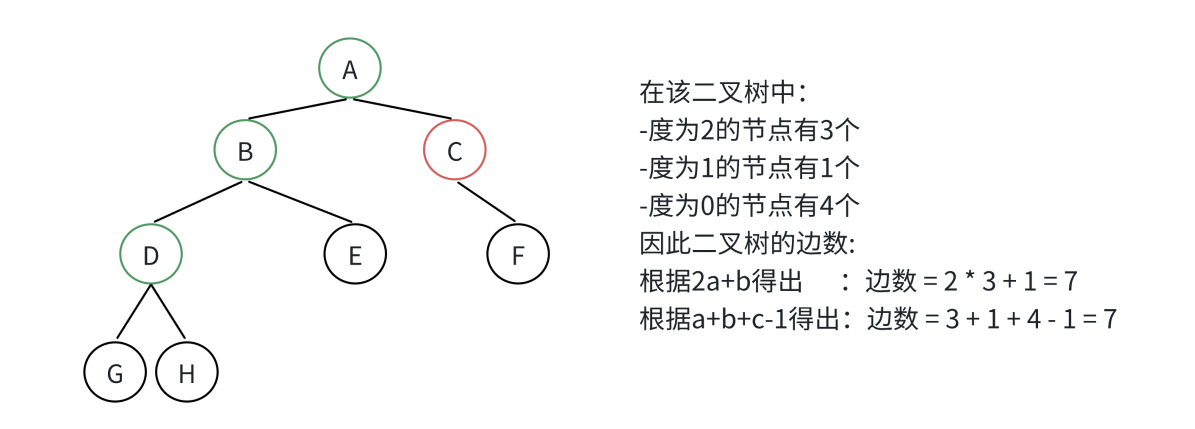
证明上述性质：

假设一个二叉树有 a 个度为2的节点， b 个度为1的节点， c 个叶节点，则这个二叉树的边数是2a+b

另一方面，由于共有 a+b+c 个节点，所以边数等于 a+b+c-1

结合上面两个公式：

2a+b = a+b+c-1 ，即： a = c-1