class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {vector<vector<int>> ans;back(nums,0,ans);return ans;}void back(vector<int>& nums,int n,vector<vector<int>>& ans){int i;if(n==nums.size()-1)ans.push_back(nums);for(i=n;i<nums.size();i++){swap(nums[i],nums[n]);back(nums,n+1,ans);swap(nums[i],nums[n]);}}
};

77.组合

77. 组合

题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

题解

设定一个count，计算每一个的数量，当count==k时候，就放入数组。这是跟之前不太一样的，之前的是进行排列组合。这个有点像选择排列。

从1-n开始，设置一个额外的数组来存储每一次的结果。count动态变化，将i赋给后count加一，dfs中从（i+1，n）选一个数字。回溯后count--。

class Solution {
public:vector<vector<int>> combine(int n, int k) {vector<vector<int>> ans;vector<int> c(k,0);int count;dfs(n,k,1,ans,c,count);return ans;}void dfs(int n,int k,int level,vector<vector<int>>& ans,vector<int>& c,int& count){int i;if(count==k){ans.push_back(c);return ;}for(i=level;i<=n;i++){c[count++]=i;dfs(n,k,i+1,ans,c,count);--count;}}
};

79.单位搜索

79. 单词搜索

题目

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

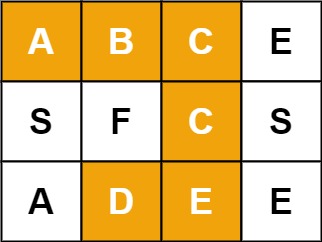
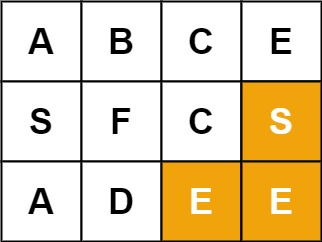
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

题解

类似的套路。

dfs+回溯法，首先定义一个visit，来标记每一次搜索的时候该位置是否被标记过，防止同一个位置被多次访问。

对于一个位置，要进行边界判断，是否越界。接着判断是否已经访问过，是否已经成功找到，是否该位置的字母与目标字母不同。

dfs，往四周搜索。

class Solution {
public:bool exist(vector<vector<char>>& board, string word) {if(board.empty())return false;int m=board.size(),n=board[0].size();vector<vector<bool>> visit(m,vector<bool>(n,false));int i,j;bool find=false;for(i=0;i<m;i++){for(j=0;j<n;j++)back(i,j,board,word,find,visit,0);}return find;}void back(int i,int j,vector<vector<char>>& board,string& word,bool& find,vector<vector<bool>>& visit,int level){if(i<0||i>=board.size()||j<0||j>=board[0].size())return ;if(visit[i][j]||find||board[i][j]!=word[level])return ;if(level==word.size()-1){find=true;return ;}visit[i][j]=true;back(i+1,j,board,word,find,visit,level+1);back(i-1,j,board,word,find,visit,level+1);back(i,j+1,board,word,find,visit,level+1);back(i,j-1,board,word,find,visit,level+1);visit[i][j]=false;}
};

51.N皇后

51. N 皇后

题目

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

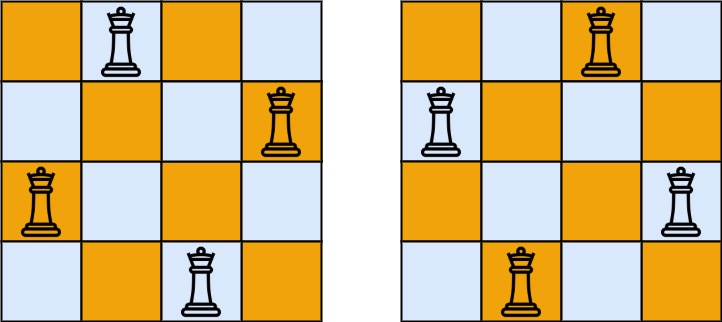
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9

题意

N皇后，需要三个标记函数，一个是列，一个是主对角线，另外一个是副对角线。

因为每一行肯定会放一个皇后，一行一行遍历，当成功遍历到最后一行并且成功放好皇后即可。所以不需要设行的标记函数。

这个时候我们可以从第一行开始，按列遍历。判断该列是否为false，该主对角线是否为false，副对角线是否为false。如果是则下一列，如果不是就将该位置置为Q，然后对下一行进行同样的寻找。回溯法，找完后记得将位置和标记函数还原。

这个对角线和副对角线。可以画在坐标上，一个为y=x+b，一个为y=-x+b。

所以b=y-x，为了使b>0，因此我们加上n。另外一个为y+x。

class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<vector<string>> ans;if(n==0)return {};vector<string> board(n,string(n,'.'));vector<bool> c(n,false),l(2*n-1,false),r(2*n-1,false);back(n,ans,board,c,l,r,0);return ans;}void back(int n,vector<vector<string>>& ans,vector<string>& board,vector<bool>& c,vector<bool>& l,vector<bool>& r,int row){if(row==n){ans.push_back(board);return ;}int i;for(i=0;i<n;i++){if(c[i]||l[row-i+n]||r[row+i]){continue;}board[row][i]='Q';c[i]=l[row-i+n]=r[row+i]=true;back(n,ans,board,c,l,r,row+1);board[row][i]='.';c[i]=l[row-i+n]=r[row+i]=false;}}
};

总结

对于回溯法，首先找到边界条件以及结束的条件。一般为设置的i等于行数。

边界条件一般为不要越界。

一般还需要设置标记函数。然后一行一行进行访问或者一个位置一个位置的访问，访问过的标记函数置为true。接着继续下一个或者下一行（一般是递归）。然后结束后还原上面的标记函数以及board（一般会设置一个作为答案）。符合的就push_back到ans数组中去。