深入理解 go map

什么是 map

维基百科里这样定义 map：

In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.

简单说明一下：在计算机科学里，被称为相关数组、map、符号表或者字典，是由一组 <key, value> 对组成的抽象数据结构，，并且同一个 key 只会出现一次。

map 的设计也被称为 “The dictionary problem”，它的任务是设计一种数据结构用来维护一个集合的数据，并且可以同时对集合进行增删查改的操作。

哈希表是计算机科学中的最重要数据结构之一，这不仅因为它 𝑂(1)𝑂(1) 的读写性能非常优秀，还因为它提供了键值之间的映射。想要实现一个性能优异的哈希表，需要注意两个关键点 —— 哈希函数和冲突解决方法。

哈希函数

实现哈希表的关键点在于哈希函数的选择，哈希函数的选择在很大程度上能够决定哈希表的读写性能。在理想情况下，哈希函数应该能够将不同键映射到不同的索引上，这要求哈希函数的输出范围大于输入范围，但是由于键的数量会远远大于映射的范围，所以在实际使用时，这个理想的效果是不可能实现的。

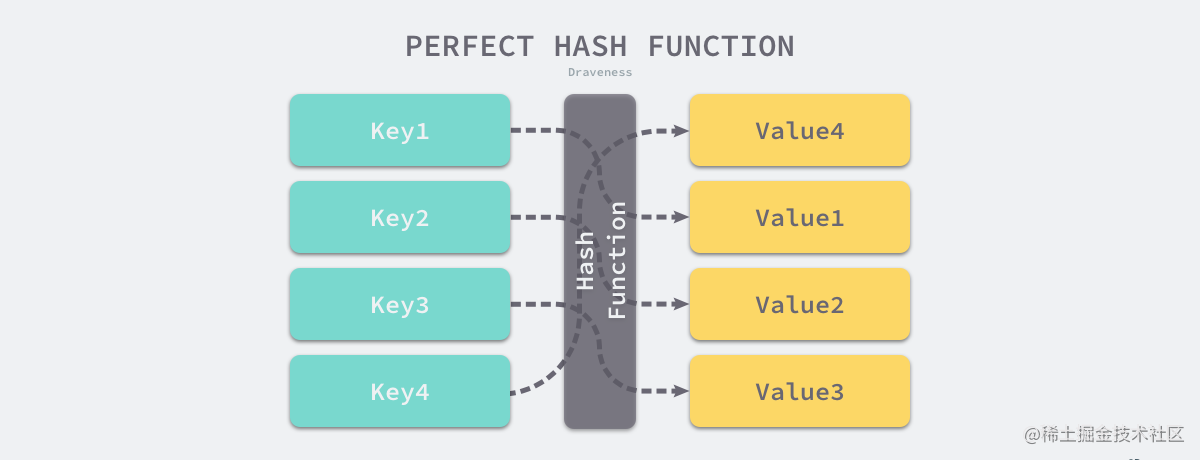
完美哈希函数

比较实际的方式是让哈希函数的结果能够尽可能的均匀分布，然后通过工程上的手段解决哈希碰撞的问题。哈希函数映射的结果一定要尽可能均匀，结果不均匀的哈希函数会带来更多的哈希冲突以及更差的读写性能。

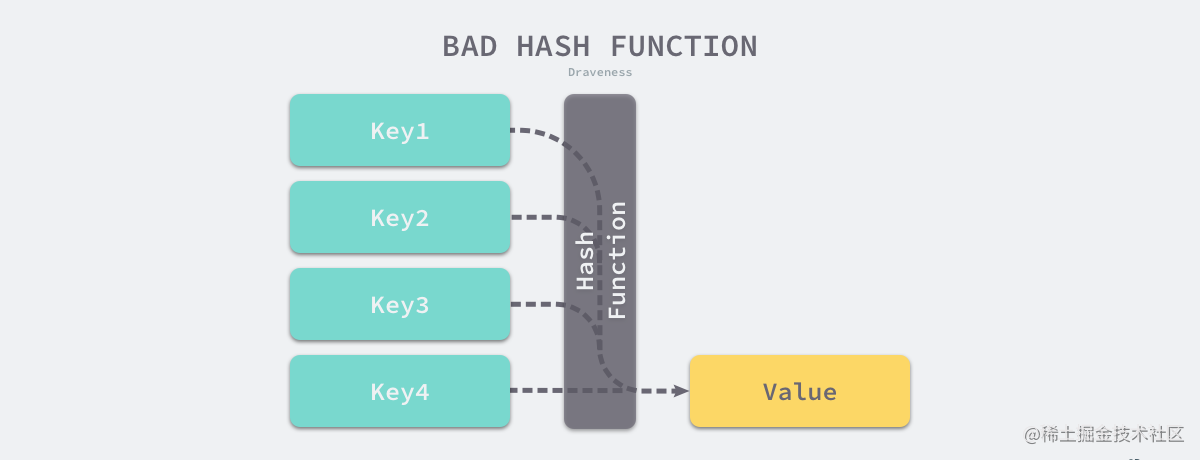
不均匀哈希函数

如果使用结果分布较为均匀的哈希函数，那么哈希的增删改查的时间复杂度为 𝑂(1)；但是如果哈希函数的结果分布不均匀，那么所有操作的时间复杂度可能会达到 𝑂(𝑛)，由此看来，使用好的哈希函数是至关重要的。

冲突解决

就像我们之前所提到的，在通常情况下，哈希函数输入的范围一定会远远大于输出的范围，所以在使用哈希表时一定会遇到冲突，哪怕我们使用了完美的哈希函数，当输入的键足够多也会产生冲突。然而多数的哈希函数都是不够完美的，所以仍然存在发生哈希碰撞的可能，这时就需要一些方法来解决哈希碰撞的问题，常见方法的就是开放寻址法和拉链法。

开放寻址法

开放寻址法是一种在哈希表中解决哈希碰撞的方法，这种方法的核心思想是依次探测和比较数组中的元素以判断目标键值对是否存在于哈希表中，如果我们使用开放寻址法来实现哈希表，那么实现哈希表底层的数据结构就是数组，不过因为数组的长度有限，向哈希表写入 (author, draven) 这个键值对时会从如下的索引开始遍历：

index := hash("author") % array.len

当我们向当前哈希表写入新的数据时，如果发生了冲突，就会将键值对写入到下一个索引不为空的位置：

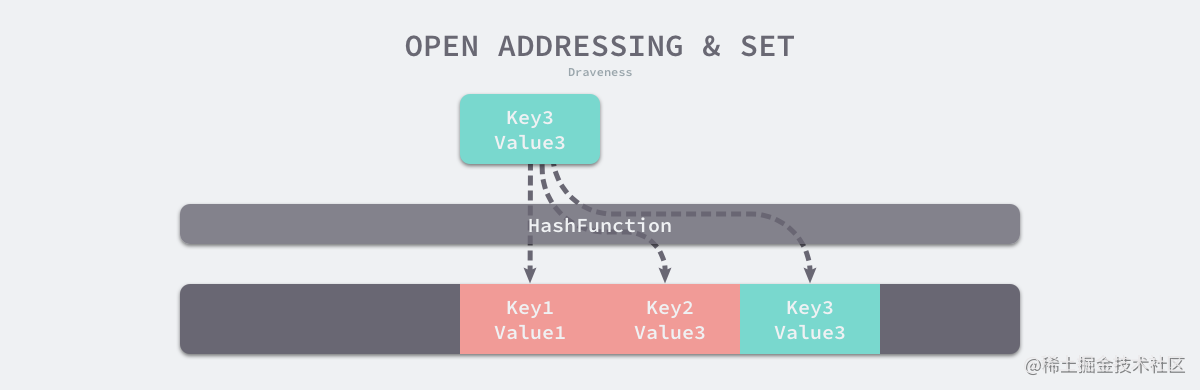
开放地址法写入数据

如上图所示，当 Key3 与已经存入哈希表中的两个键值对 Key1 和 Key2 发生冲突时，Key3 会被写入 Key2 后面的空闲位置。当我们再去读取 Key3 对应的值时就会先获取键的哈希并取模，这会先帮助我们找到 Key1，找到 Key1 后发现它与 Key 3 不相等，所以会继续查找后面的元素，直到内存为空或者找到目标元素。

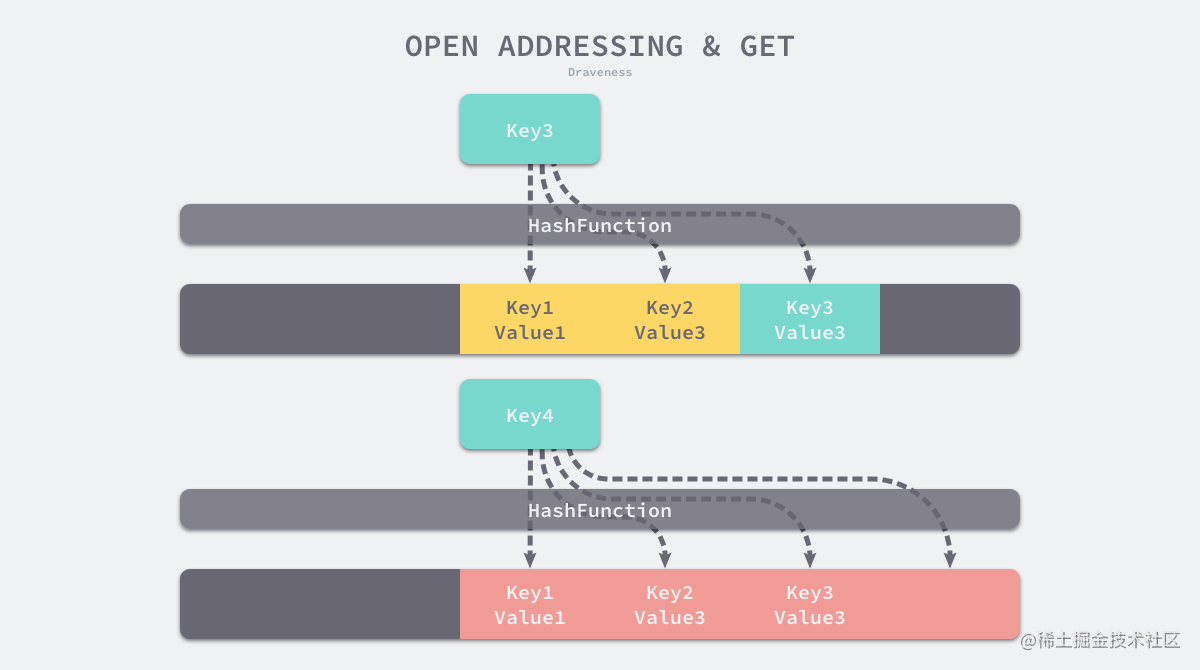
开放地址法读取数据

当需要查找某个键对应的值时，会从索引的位置开始线性探测数组，找到目标键值对或者空内存就意味着这一次查询操作的结束。

开放寻址法中对性能影响最大的是装载因子，它是数组中元素的数量与数组大小的比值。随着装载因子的增加，线性探测的平均用时就会逐渐增加，这会影响哈希表的读写性能。当装载率超过 70% 之后，哈希表的性能就会急剧下降，而一旦装载率达到 100%，整个哈希表就会完全失效，这时查找和插入任意元素的时间复杂度都是 𝑂(𝑛) 的，这时需要遍历数组中的全部元素，所以在实现哈希表时一定要关注装载因子的变化。

拉链法

与开放地址法相比，拉链法是哈希表最常见的实现方法，大多数的编程语言都用拉链法实现哈希表，它的实现比较开放地址法稍微复杂一些，但是平均查找的长度也比较短，各个用于存储节点的内存都是动态申请的，可以节省比较多的存储空间。

实现拉链法一般会使用数组加上链表，不过一些编程语言会在拉链法的哈希中引入红黑树以优化性能，拉链法会使用链表数组作为哈希底层的数据结构，我们可以将它看成可以扩展的二维数组：

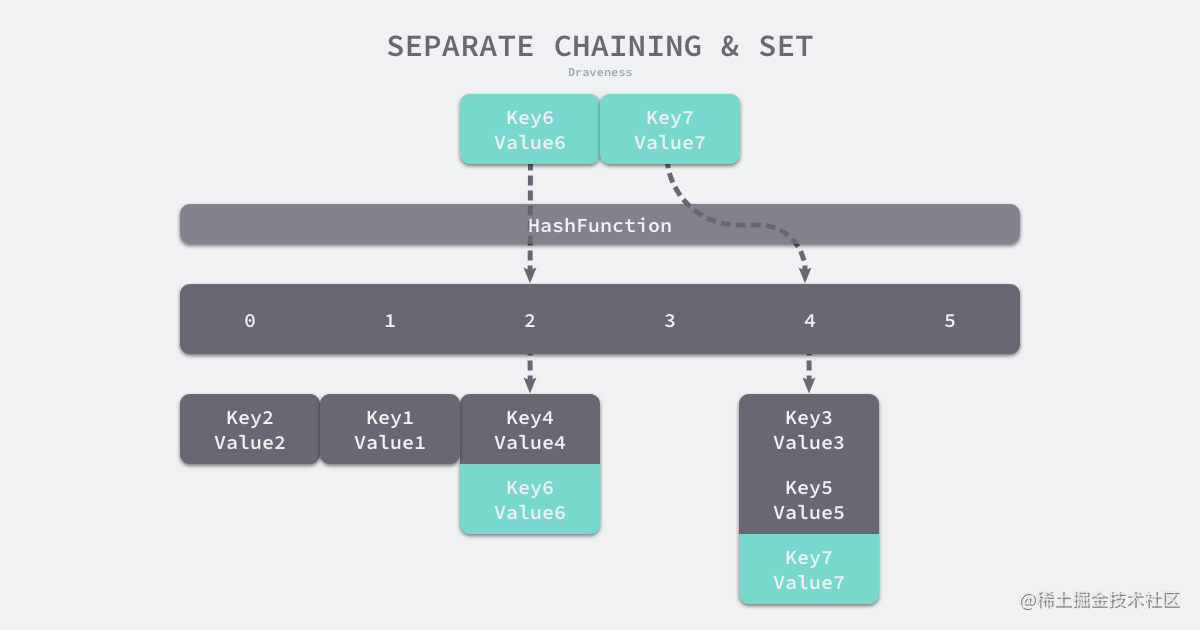
拉链法写入数据

如上图所示，当我们需要将一个键值对 (Key6, Value6) 写入哈希表时，键值对中的键 Key6 都会先经过一个哈希函数，哈希函数返回的哈希会帮助我们选择一个桶，和开放地址法一样，选择桶的方式是直接对哈希返回的结果取模：

index := hash("Key6") % array.len

选择了 2 号桶后就可以遍历当前桶中的链表了，在遍历链表的过程中会遇到以下两种情况：

找到键相同的键值对 — 更新键对应的值；
没有找到键相同的键值对 — 在链表的末尾追加新的键值对；

如果要在哈希表中获取某个键对应的值，会经历如下的过程：

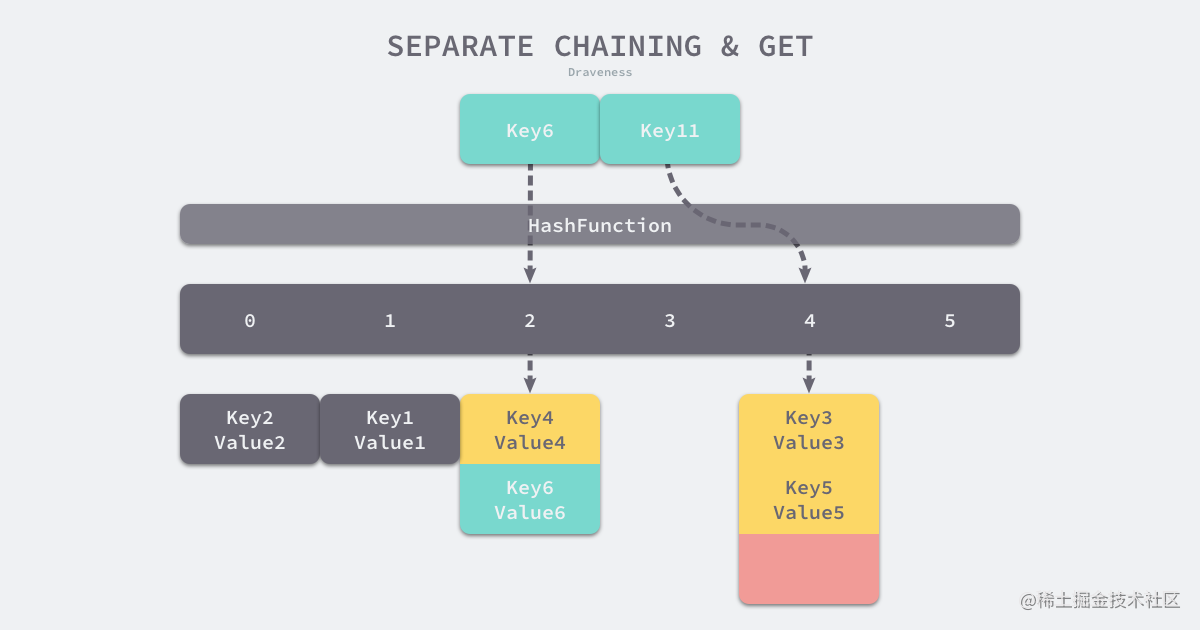
拉链法读取数据

Key11 展示了一个键在哈希表中不存在的例子，当哈希表发现它命中 4 号桶时，它会依次遍历桶中的链表，然而遍历到链表的末尾也没有找到期望的键，所以哈希表中没有该键对应的值。

在一个性能比较好的哈希表中，每一个桶中都应该有 0~1 个元素，有时会有 2~3 个，很少会超过这个数量。计算哈希、定位桶和遍历链表三个过程是哈希表读写操作的主要开销，使用拉链法实现的哈希也有装载因子这一概念：

装载因子:=元素数量÷桶数量装载因子:=元素数量÷桶数量

与开放地址法一样，拉链法的装载因子越大，哈希的读写性能就越差。在一般情况下使用拉链法的哈希表装载因子都不会超过 1，当哈希表的装载因子较大时会触发哈希的扩容，创建更多的桶来存储哈希中的元素，保证性能不会出现严重的下降。如果有 1000 个桶的哈希表存储了 10000 个键值对，它的性能是保存 1000 个键值对的 1/10，但是仍然比在链表中直接读写好 1000 倍。

map 内存模型

在源码中，表示 map 的结构体是 hmap，它是 hashmap 的“缩写”：

// A header for a Go map.
type hmap struct {// 元素个数，调用 len(map) 时，直接返回此值count     intflags     uint8// buckets 的对数 log_2B         uint8// overflow 的 bucket 近似数noverflow uint16// 计算 key 的哈希的时候会传入哈希函数hash0     uint32// 指向 buckets 数组，大小为 2^B// 如果元素个数为0，就为 nilbuckets    unsafe.Pointer// 扩容的时候，buckets 长度会是 oldbuckets 的两倍oldbuckets unsafe.Pointer// 指示扩容进度，小于此地址的 buckets 迁移完成nevacuate  uintptrextra *mapextra // optional fields
}

说明一下，B 是 buckets 数组的长度的对数，也就是说 buckets 数组的长度就是 2^B。bucket 里面存储了 key 和 value，后面会再讲。

buckets 是一个指针，最终它指向的是一个结构体：

type bmap struct {tophash [bucketCnt]uint8
}

但这只是表面(src/runtime/hashmap.go)的结构，编译期间会给它加料，动态地创建一个新的结构：

type bmap struct {topbits  [8]uint8keys     [8]keytypevalues   [8]valuetypepad      uintptroverflow uintptr
}

bmap 就是我们常说的“桶”，桶里面会最多装 8 个 key，这些 key 之所以会落入同一个桶，是因为它们经过哈希计算后，哈希结果是“一类”的。在桶内，又会根据 key 计算出来的 hash 值的高 8 位来决定 key 到底落入桶内的哪个位置（一个桶内最多有8个位置）。

来一个整体的图：

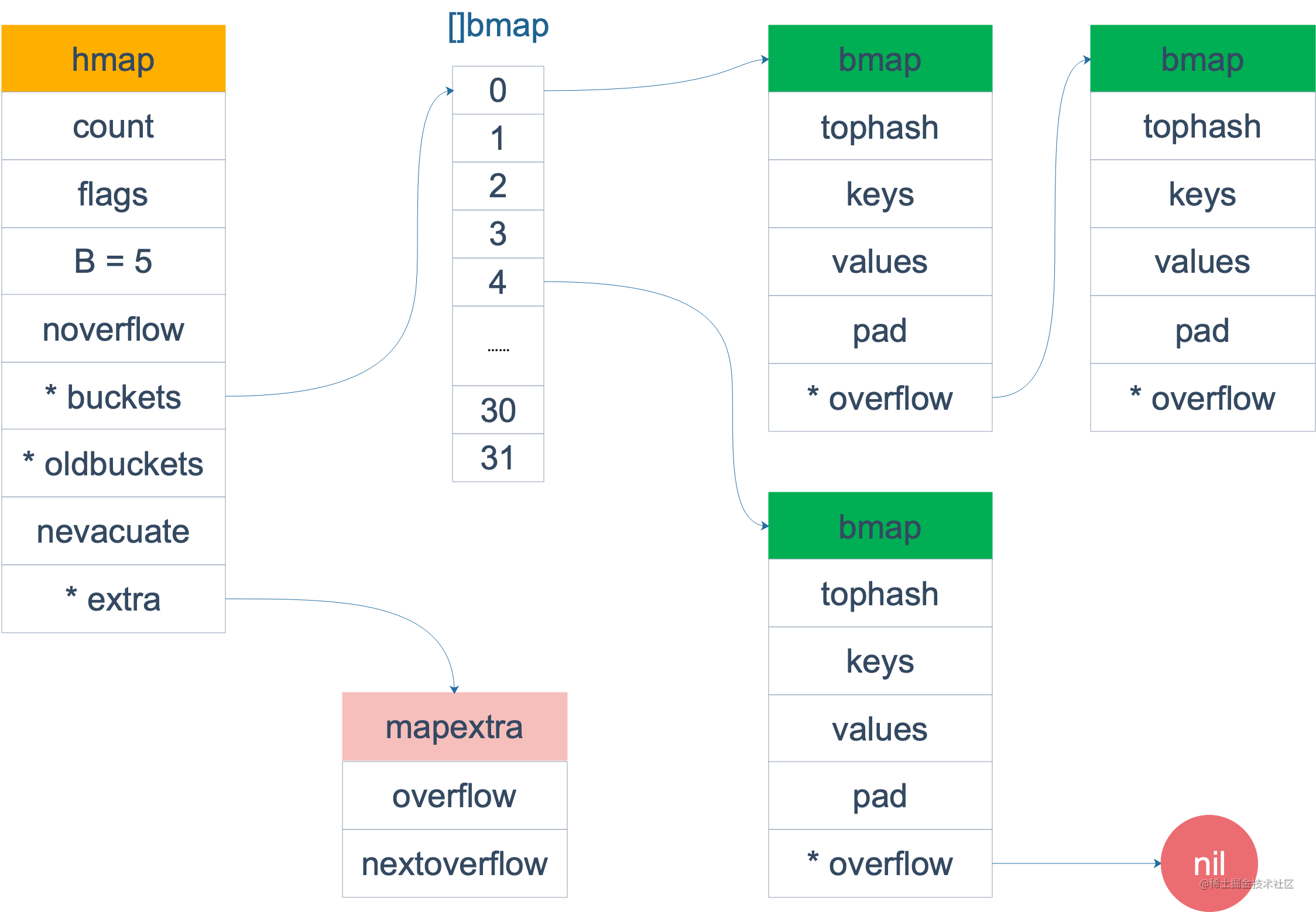
当 map 的 key 和 value 都不是指针，并且 size 都小于 128 字节的情况下，会把 bmap 标记为不含指针，这样可以避免 gc 时扫描整个 hmap。但是，我们看 bmap 其实有一个 overflow 的字段，是指针类型的，破坏了 bmap 不含指针的设想，这时会把 overflow 移动到 extra 字段来。

type mapextra struct {// overflow[0] contains overflow buckets for hmap.buckets.// overflow[1] contains overflow buckets for hmap.oldbuckets.overflow [2]*[]*bmap// nextOverflow 包含空闲的 overflow bucket，这是预分配的 bucketnextOverflow *bmap}

bmap 是存放 k-v 的地方，我们把视角拉近，仔细看 bmap 的内部组成: