图论·Day01

P3371
P4779

P3371 【模板】单源最短路径（弱化版）

注意的点：

边有重复，选择最小边！
对于SPFA算法容易出现重大BUG，没有负权值的边时不要使用！！！

70分代码朴素板dijsktra

爆空间

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
void solve() {cin >> n >> m >> s;vector<vector<int>>grid(n + 9, vector<int>(n + 9, INT_MAX));vector<int>dist(n + 9, INT_MAX);vector<bool>visited(n + 9, false);while (m--) {cin >> u >> v >> w;grid[u][v] = min(grid[u][v], w);}dist[s] = 0;for (int i = 1; i <= n; i++) {int cur = 1;int minDist = INT_MAX;for (int j = 1; j <= n; j++) {if (!visited[j] && dist[j] < minDist) {minDist = dist[j];cur = j;}}visited[cur] = true;for (int j = 1; j <= n; j++) {if (!visited[j] && grid[cur][j] != INT_MAX && dist[cur] + grid[cur][j] < dist[j]) {dist[j] = dist[cur] + grid[cur][j];}}/*cout << "select " << cur << endl;for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}cout << endl;*/}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}

32分代码 SPFA

因为有重复指向的边，所有理论上边数可以无穷大，O(KM)的时间复杂度不确定性极大！

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {}
};
void solve() {cin >> n >> m >> s;vector<list<Edge>>grid(n + 9, list<Edge>());vector<int>dist(n + 9, INT_MAX); dist[s] = 0;queue<Edge>q;while (m--) {cin >> u >> v >> w;grid[u].push_back(Edge(v, w));}q.push({ s,0 });while (!q.empty()) {Edge cur = q.front();q.pop();for (auto item : grid[cur.v]) {if (item.w + dist[cur.v] < dist[item.v]) {dist[item.v] = dist[cur.v] + item.w;q.push(item);}}}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}

AC代码堆优化dijsktra

重复的边不影响

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {}
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;//从小排序}
};void solve() {cin >> n >> m >> s;vector<list<Edge>>grid(n + 9, list<Edge>());vector<int>dist(n + 9, INT_MAX); dist[s] = 0;vector<bool>visited(n + 9, false);priority_queue<Edge, vector<Edge>, cmp>q;while (m--) {cin >> u >> v >> w;grid[u].push_back(Edge(v, w));}q.push({ s,0 });while (!q.empty()) {Edge cur = q.top();q.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : grid[cur.v]) {if (!visited[item.v]&&item.w + dist[cur.v] < dist[item.v]) {dist[item.v] = item.w + dist[cur.v];q.push({ item.v,dist[item.v] });}}}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}

P1144

最短路计数

题目描述

给出一个 $N$ 个顶点 $M$ 条边的无向无权图，顶点编号为 $1\sim N$ 。问从顶点 $1$ 开始，到其他每个点的最短路有几条。

输入格式

第一行包含 $2$ 个正整数 $N, M$ ，为图的顶点数与边数。

接下来 $M$ 行，每行 $2$ 个正整数 $x, y$ ，表示有一条连接顶点 $x$ 和顶点 $y$ 的边，请注意可能有自环与重边。

输出格式

共 $N$ 行，每行一个非负整数，第 $i$ 行输出从顶点 $1$ 到顶点 $i$ 有多少条不同的最短路，由于答案有可能会很大，你只需要输出 $ ans \bmod 100003$ 后的结果即可。如果无法到达顶点 $i$ 则输出 $0$ 。

对于 $100\%$ 的数据， $1\le N\le10^6$ ， $1\le M\le 2\times 10^6$ 。

AC题解堆优化dijsktra

多一段条件判断，不加入堆但是也起到了统计作用

else if (dist[cur.v] + item.w == dist[item.v]) {ct[item.v] += ct[cur.v];ct[item.v] %= 100003;}

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, x, y;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {};
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;}
};
priority_queue<Edge,vector<Edge>,cmp>q;
void solve() {cin >> n >> m;vector<list<Edge>>grid(n+ 9, list<Edge>());vector<bool>visited(n+ 9, false);vector<int>dist(n+9, INT_MAX);vector<int>ct(n+9, 0);while (m--) {cin >> x >> y;grid[x].push_back(Edge(y, 1));grid[y].push_back(Edge(x, 1));}dist[1] = 0; ct[1] = 1;q.push({ 1,0 });while (!q.empty()) {Edge cur=q.top();q.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : grid[cur.v]) {if (dist[cur.v] + item.w < dist[item.v]) {dist[item.v] = dist[cur.v] + item.w;ct[item.v] = ct[cur.v];q.push({ item.v,dist[item.v] });}else if (dist[cur.v] + item.w == dist[item.v]) {ct[item.v] += ct[cur.v];ct[item.v] %= 100003;}}}//for (int i = 1; i <= n; i++) {//    cout << dist[i] << " ";//}for (int i = 1; i <= n; i++) {cout << ct[i] << endl;}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}

P5905

【模板】全源最短路（Johnson）

题目描述

给定一个包含 $n$ 个结点和 $m$ 条带权边的有向图，求所有点对间的最短路径长度，一条路径的长度定义为这条路径上所有边的权值和。

注意：

边权可能为负，且图中可能存在重边和自环；
部分数据卡 $n$ 轮 SPFA 算法。

输入格式

第 $1$ 行： $2$ 个整数 $n, m$ ，表示给定有向图的结点数量和有向边数量。

接下来 $m$ 行：每行 $3$ 个整数 $u, v, w$ ，表示有一条权值为 $w$ 的有向边从编号为 $u$ 的结点连向编号为 $v$ 的结点。

输出格式

若图中存在负环，输出仅一行 $- 1$ 。

若图中不存在负环：

输出 $n$ 行：令 $dis_{i,j}$ 为从 $i$ 到 $j$ 的最短路，在第 $i$ 行输出 $\sum\limits_{j=1}^n j\times dis_{i,j}$ ，注意这个结果可能超过 int 存储范围。

如果不存在从 $i$ 到 $j$ 的路径，则 $dis_{i,j}=10^9$ ；如果 $i = j$ ，则 $dis_{i,j}=0$ 。

右图为样例 $2$ 给出的有向图，红色标注的边构成了负环，注意给出的图不一定连通。

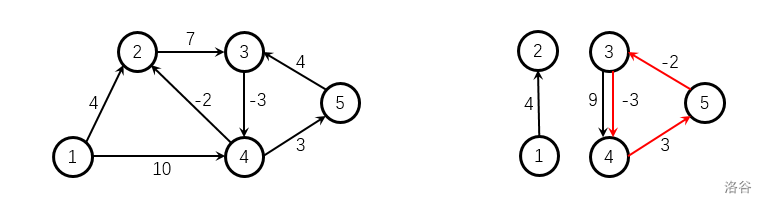
Johnson算法

数据溢出longlong的转换
h[item.v] = h[cur.v] + item.w;这段代码是Johnson算法的精髓，势能函数
dist[j] + h[j] - h[st]由于路径上每一个边<i,j>都加入了h[i]-h[j],所以最短距离应该要 + 末位 - 首位，才是最终距离！

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m;
ll u,v,w;
void dijsktra(int st,vector<ll>dist);
struct Edge {ll v, w;Edge(ll a, ll b) :v(a), w(b) {};
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;}
};
ll inf = ll(1e9);
queue<Edge>q;
vector<int>ct(3009, 0);
vector<list<Edge>>edges(3009, list<Edge>());
vector<ll>h(3009, inf);vector<ll>dist(3009, inf);
priority_queue<Edge, vector<Edge>, cmp>s;
bool visited[3009];
void solve() {cin >> n >> m;while(m--) {cin >> u >> v >> w;edges[u].push_back({ v,w });}for (int i = 1; i <= n; i++) {edges[0].push_back({ i,0 });}h[0] = 0;q.push({ 0,0 }); ct[0] = 1;while (!q.empty()) {Edge cur = q.front();q.pop();if (ct[cur.v] >= n) {cout << -1;return;}for (auto item : edges[cur.v]) {if (h[cur.v] + item.w < h[item.v]) {h[item.v] = h[cur.v] + item.w;ct[item.v] ++;q.push(item);              }}}/*  cout << "h" << endl;for (int i = 0; i <= n; i++) {cout << h[i]<<" ";}cout << endl;*//*重组edges数组*/for (int i = 1; i <= n; i++) {for (auto& item : edges[i]) {item.w = item.w+h[i] - h[item.v];}}for (int i = 1; i <= n; i++) {dijsktra(i,dist);}
}
void dijsktra(int st,vector<ll>dist) {memset(visited, false, sizeof(visited));dist[st] = 0; s.push({ st,0 });while (!s.empty()) {Edge cur = s.top();s.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : edges[cur.v]) {if (!visited[item.v]&&dist[cur.v] + item.w < dist[item.v]) {dist[item.v] = item.w+ dist[cur.v];s.push({ item.v,dist[item.v] });}}}/*for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}cout << endl;*/ll ans = 0;for (int j = 1; j <= n; j++) {if (dist[j] == inf) {ans += ll(j) * dist[j];}else {ans += ll(j) * (dist[j] + h[j] - h[st]);}}cout << ans << endl;
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}

今日总结

dijsktra不能用于负权值
Bellman可以用于检测负权回路
SFPA算法不要轻易用！容易爆死！
Floyd 算法时间复杂度O(n3),dijsktra O(mlogm),Johnson算法时间复杂度接近 O(nmlogn)，相当于用SFPA扫除了dijsktra不能求负权值边的障碍，最终还是要归结于dijsktra算法堆优化版来！说人话就是Bellman和SFPA太慢，dijsktra用不了，所以采用Johnson算法！