Chap2 性能评测和并行编程

性能评测

作业题会用到，考试没考过。

$CPI=\frac{执行整个程序所需的时钟周期数}{程序中指令总数}$，即：

$$CPI=\frac{{\sum }_{i=1}^n(CP{I}_i\times I_i)}{I_N}$$

时钟频率 $R_C$ ， $MIPS$ （每秒百万条指令）为：

$$MIPS=\frac{R_C}{CPI\times 10^6}$$

$CPU执行时间=总时钟周期数\times 时钟周期=\frac{总时钟周期数}{时钟频率}$，即：

$$T_{CPU}=\frac{T_C}{R_C}$$

并行编程

共享地址空间方法中，常见的同步原语有：

• 锁（提供互斥）：临界区中一次只能有一个线程；
• 障碍（提供同步）：等待线程到达此点。障碍是表达依赖关系的一种保守方式。障碍将计算分为多个阶段，障碍之前所有线程的所有计算在障碍开始后任何线程中的任何计算之前完成。换句话说，假设障碍之后的所有计算都依赖于障碍之前的所有计算。

int n;
bool done = false;
float diff = 0.0;
LOCK myLock;
BARRIER myBarrier;//allocate grid
float* A = allocate(n+2, n+2);void solve(float* A){float myDiff;int myMin = 1+(threadId*n/NUM_PROCESSORS);int myMax = myMin + (n/NUM_PROCESSORS);while(!done){float myDiff = 0.f;diff = 0.f;barrier(myBarrier,NUM_PROCESSORS);for(j=myMin to myMax){for(i = red cells in this row){float prev = A[i,j];A[i,j] = 0.2f * (A[i-1,j]+A[i,j-1]+A[i,j]+A[i+1,j]+A[i,j+1]);myDiff += abs(A[i,j]-prev);}lock(myLock);diff += myDiff;unlock(myLock);barrier(myBarrier,NUM_PROCESSORS);if(diff/(n*n) < TOLERANCE) // checkdone = true;barrier(myBarrier,NUM_PROCESSORS);}}
}

为什么需要三次 barrier

本示例使用了多个处理器来加速计算过程，代码中的 barrier 函数调用是同步点，每个 barrier 都是必要的，它们确保了在关键的计算步骤之间所有线程的同步，防止数据冲突和不一致的结果。

• 第一次 barrier 用于等待所有线程都完成初始化，确保 diff 变量在 for 循环计算之前为 0.f。
• 第二次 barrier 用于等待所有线程都更新全局变量 diff ，每一轮迭代中，diff 是所有线程的 myDiff 变量之和。
• 第三次 barrier 用于等待所有线程检查是否满足了收敛条件，确保每个线程对 done 变量的操作相同。

此外，lock 的使用是为了保护共享资源 diff，确保在任何时刻只有一个线程可以更新这个变量。

改进方法

• 在连续的循环迭代中使用不同的 diff 变量来删除依赖关系；
• 权衡占用空间以消除依赖关系（一种常见的并行计算技巧）。

这种技巧是指在并行编程中，通过牺牲一些内存占用来减少或消除数据之间的依赖关系，从而提高并行性和性能。这通常涉及到复制或重复存储一些数据，以便每个线程或处理器都可以独立地访问和操作它们，而无需等待其他线程或处理器的输入或结果。

int n; // grid size
bool done = false;
LOCK myLock;
BARRIER myBarrier;
float diff[3]; // global diff, but now 3 copiesfloat *A = allocate(n+2, n+2);void solve(float* A) {float myDiff; // thread local variableint index = 0; // thread local variablediff[0] = 0.0f;barrier(myBarrier, NUM_PROCESSORS); // one-time only: just for initwhile (!done) {myDiff = 0.0f;// 这里不再需要 barrier 确保全局 diff 初始化为 0.f//// perform computation (accumulate locally into myDiff)//lock(myLock);diff[index] += myDiff; // atomically update global diffunlock(myLock);diff[(index+1) % 3] = 0.0f;barrier(myBarrier, NUM_PROCESSORS);  // 这个barrier既等待全局diff[index]的值，又初始化全局diff[(index+1)%3]的值为0.fif (diff[index]/(n*n) < TOLERANCE)  break;// 这里不再需要barrier确保各线程对全局done进行相同操作，直接breakindex = (index + 1) % 3;}
}

Chap3 互连网络

交换和路由

二维网格中 XY 路由

如果发送方节点的坐标为 $(X_1,Y_1)$，接收方节点的坐标为 $(X_2,Y_2)$，那么消息会首先沿着 $X$ 轴移动到达 $X$ 坐标为 $X_2$ 的位置，然后再沿着 $Y$ 轴移动到达 $Y$ 坐标为 $Y_2$ 的位置。

以左下角的节点为 $(0,0)$ 坐标，建立 XY 轴。

算法：二维网格中 XY 路由
输入：当前节点的坐标(Xcurrent,Ycurrent)和目标节点的坐标(Xdest,Ydest)
输出：选择的输出通道Channel
过程：Xoffest := Xdest - Xcurrent;Yoffset := Ydest - Ycurrent;if Xoffset < 0 thenChannel := X- ;endifif Xoffret > 0 thenChannel:= X+;endifif Xoffset = 0 and Yoffset < 0 thenChannel := Y-;endifif Xoffset = 0 and Yoffset > 0 thenChannel := Y+;endifit Xoffset = 0 and Yoffset = 0 thenChannel := Internal;  //Internal是连接本地节点的通道endif

死锁、活锁及饿死

关键原因都是因为资源有限。

• 死锁是指两个或多个进程（或报文）因为互相等待对方释放资源而无法继续执行的状态。包含在死锁配置内的所有报文将永远被阻塞。

• 活锁指的是系统中的进程（或报文）一直在重试某个操作，但是却无法取得进展，因此系统不能正常工作。

• 如果网络流量紧张，某个报文由于所请求的资源总是分配给其他请求同一资源的报文，该报文也会被阻塞，这种情况称为饿死。

死锁避免的方法：虚通道、转弯模型

虚通道：将一条物理通道分成多条逻辑通道（虚通道）复用，交换机内的缓冲也相应分成多份。目的是减少死锁。如，单向二维环绕网的维序路由。

转弯模型：禁止最小数量的转弯，防止环的出现，从而避免发生死锁。如二维网格中最小 西向优先、北向最后和负向优先算法

二维网格中最小 西向优先、北向最后和负向优先算法

在二维网格中，通道的方向通常是根据坐标轴来定义的，其中 X- 代表西向，Y+代表北向。

三种合法转弯选路方法：

• 西向优先：不允许转向 X- 方向；

• 北向最后：不允许来自 Y+ 方向的转弯；

• 负向优先：禁止从负方向转向正方向。

总结：策略优先，XY 路由次之。

例如，西向优先，那么优先考虑 Xoffset < 0，再考虑 Xoffset > 0，最后是 Xoffset = 0，这三种情况分别对应 Yoffset < 0、 Yoffset > 0 和 Yoffset = 0。

1. 最小西向优先算法：如果需要向西路由，先向西路由一个包，然后自适应地向南、向北、向东路由。

算法：二维网格中最小西向优先算法
输入：当前节点的坐标(Xcurrent,Ycurrent)和目标节点的坐标(Xdest,Ydest)
输出：选择的输出通道Channel
过程：Xoffest := Xdest - Xcurrent;Yoffset := Ydest - Ycurrernt;If Xoffset < 0 then Channel := X-;endifIf Xoffset › 0 and Yoffset < 0 thenChannel := Select (X+, Y-) ;  // Select 选择函数，从通道中选择一个空闲的通道endifIf Xoffset > 0 and Yoffset > 0 thenChannel := Select ( X+, Y+);endifif Xoffset > 0 and Yoffset = 0 thenChannel := X+;endifif Xoffset = 0 and Yoffset < 0 thenChannel := Y-;endifIf Xoffset = 0 and Yoffset > 0 thenChannel := Y+;endifIf Xoffset = 0 and Yoffset = 0 then Channel := Internal;  //Internal是连接本地节点的通道endif

2. 北最后算法的思想是在选择输出通道时，尽可能避免向北方向移动，除非没有其他选项。这种算法适用于那些希望最小化北向移动的场景，例如在某些网络拓扑中，北向通道可能比其他方向更拥挤或者成本更高。

在伪代码中，首先检查东西方向（X轴）的偏移量，如果目标在当前节点的西边（Xoffset < 0），则优先选择西向通道（X-）。如果目标在东边（Xoffset > 0），则选择东向通道（X+）。只有当目标正好在当前节点的正北方或正南方时（Xoffset = 0），我们才考虑北向或南向的移动。如果目标在南边（Yoffset < 0），则选择南向通道（Y-），如果在北边（Yoffset > 0），则最后考虑北向通道（Y+）。如果当前节点就是目标节点（Xoffset = 0 and Yoffset = 0），则选择内部通道（Internal）。

算法：二维网格中最小北向最后算法
输入：当前节点的坐标(Xcurrent,Ycurrent)和目标节点的坐标(Xdest,Ydest)
输出：选择的输出通道Channel
过程：Xoffest := Xdest - Xcurrent;Yoffset := Ydest - Ycurrernt;If Xoffset < 0 and Yoffset >= 0 then Channel := X-;endifIf Xoffset < 0 and Yoffset < 0 thenChannel := Select (X-, Y-);endifIf Xoffset › 0 and Yoffset >= 0 thenChannel := X+;endifif Xoffset > 0 and Yoffset < 0 thenChannel := Select (X+, Y-);endifIf Xoffset = 0 and Yoffset > 0 thenChannel := Y+;endifif Xoffset = 0 and Yoffset < 0 thenChannel := Y-;endifIf Xoffset = 0 and Yoffset = 0 then Channel := Internal;  //Internal是连接本地节点的通道endif

3. 最小负向优先算法：基本思想是，一正一负先走负，正正负负随便选。

算法：二维网格中最小负向优先算法
输入：当前节点的坐标(Xcurrent,Ycurrent)和目标节点的坐标(Xdest,Ydest)
输出：选择的输出通道Channel
过程：
Xoffset := Xdest – Xcurrent;
Yoffset := Ydest – Ycurrent;If Xoffser < 0 and Yoffset < 0channel := select(X-, Y-); // 选择函数，从通道中选择一个空闲的通道
EndifIf Xoffset < 0 and Yoffset >= 0channel := X-;
Endifif Xoffset >= 0 and Yoffset < 0channel := Y-;
Endifif Xoffset > 0 and Yoffset > 0channel := select(X+, Y+);
Endifif Xoffset > 0 and Yoffset = 0channel := X+;
Endifif Xoffset = 0 and Yoffset > 0channel = Y+;
Endifif Xoffset = 0 and Yoffset = 0channel := internal;
Endif

转弯模型：超立方体的部分自适应路由算法（P立方路由）

二元 $n$ 立方体的源 $s=s_{n-1}{s}_{n-2}\dots s_0$ 目的 $d=d_{n-1}{d}_{n-2}\dots d_0$

集合 $E$ 由所有 $s$ 和 $d$ 有差别的维数组成， $E$ 分为两个不相交的子集 $E_0$ 和 $E_1$，对于 $E$ 中的所有 $i$，如果 $s_i=0$ 且 $d_i=1$，则 $i\in E_0$，否则 $i\in E_1$。

P立方路由的基本概念就是将路由选择分成两个阶段：

• 第一个阶段报文在 $E_0$ 中以任意维序路由
• 第二个阶段在 $E_1$ 中以任意维序路由

互连网络

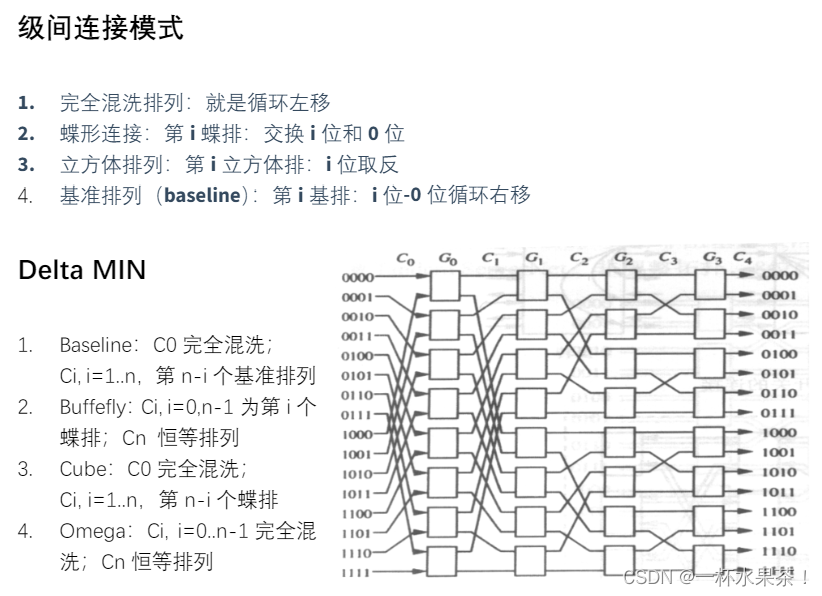
Omega 网络

OMEGA 网络采用完美洗牌互连算法，它通过循环逻辑左移位来进行数据的路由。

地址映射

考虑从 $s_{n-1}{s}_{n-2}\dots s_1{s}_0$ 到 $d_{n-1}{d}_{n-2}\dots d_1{d}_0$ 建立一条电路，

经过第 0 级链路后：$s_{n-1}{s}_{n-2}\dots s_1{s}_0$ → $s_{n-2}{s}_{n-3}\dots s_1{s}_0{s}_{n-1}$

$s_{n-2}{s}_{n-3}\dots s_1{s}_0{s}_{n-1}$ 作为第 0 级开关输入地址，

经过第 0 级开关后： $s_{n-2}{s}_{n-3}\dots s_1{s}_0{s}_{n-1}$ → $s_{n-2}{s}_{n-3}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}$

经过第 1 级链路后：$s_{n-2}{s}_{n-3}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}$ → $s_{n-3}{s}_{n-4}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}{s}_{n-2}$

$s_{n-3}{s}_{n-4}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}{s}_{n-2}$ 作为第 1 级开关输入地址，

经过第 1 级开关后： $s_{n-3}{s}_{n-4}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}{s}_{n-2}$ → $s_{n-3}{s}_{n-4}\dots s_1{s}_0{s}_{n-1}^{{}^{\prime }}{s}_{n-2}^{{}^{\prime }}$

类似的有第 $i$ 级开关的输出为： $s_{n-i-2}{s}_{n-i-3}\dots s_0{s}_{n-1}^{’}{s}_{n-2}^{’}\dots s_{n-i-1}^{’}$

从而第 $n-1$ 级开关的输出为： $s_{n-1}^{’}{s}_{n-2}^{’}\dots s_1^{’}{s}_0^{’}$

最后一级连接为恒等排列，所以 $s_{n-1}^{’}{s}_{n-2}^{’}\dots s_1^{’}{s}_0^{’}=d_{n-1}{d}_{n-2}\dots d_1{d}_0$

从而有 $s_i^{’}=d_i$

所以第 $i$ 级开关的输出为： $s_{n-i-2}{s}_{n-i-3}\dots s_0{d}_{n-1}{d}_{n-2}\dots d_{n-i-1}$

阻塞条件

对于任意两个输入/输出对 $(S,D)$ 和 $(R,T)$，可以建立无冲突的两条路径的充要条件是：

对于任意的 $i$ 都有：

$s_{n-i-2}{s}_{n-i-3}\dots s_0{d}_{n-1}{d}_{n-2}\dots d_{n-i-1}$ 不等于 $r_{n-i-2}{r}_{n-i-3}\dots r_0{t}_{n-1}{t}_{n-2}\dots t_{n-i-1}$

将两个输入/输出对的地址级联在一起，将一个大小为 $n$ 的窗口在两个输入/输出对上滑动，并对两个窗口中的内容进行比较。如果它们在任意点相等，那么两条路径在网络的某一级存在冲突。

如 （0110，1100） （1010，1111）有冲突。

自路由标记

Delta 网络的自路由特性：可以根据目的地址做出路由决策，不必考虑源地址。

自路由使用路由标志 $T=t_{n-1}..t_1{t}_0$ 执行， $t_i$ 控制 $G_i$ 级开关。

每一级路由标志都考虑哪一位是最低有效位，该位最终映射到的目标地址的相应位为哪一位，从而 $t_i$ 等于目标地址中该位的值。

在 OMEGA 网络中，在第 $i$ 级开关最低有效位为第 $n-i-1$ 位，并且最终映射到的目标地址中的对应位为第 $n-i-1$ 位，所以 $t_i=d_{n-i-1},0\le i\le n-1$

蝶形 MIN 网络

蝶式网络的特点包括：

1. 分阶段结构：网络分为多个阶段，每个阶段由一组交换节点组成。
2. 固定连接模式：每个阶段的节点按照固定的模式连接到下一个阶段的节点。
3. 重排能力：网络能够在不同的输入和输出之间建立连接，即使在多个数据包同时传输时也能避免冲突。
4. 递归结构：蝶式网络可以看作是由更小的蝶式网络递归构成，这使得它可以很容易地扩展到更大的规模。

如果两对输入/输出路径经过同一中间链路或共享任意一个中间级的同一个输出，那么这两对输入输出路径就产生冲突。

自路由标记：

在蝶形 MIN 中， $t_i=d_{i+1},(0\le i\le n-2),t_{n-1}=d_0$

阻塞条件：

如果要对于任意两个输入/输出对 $(S,D)$ 和 $(R,T)$ 建立无冲突的两条路径，其充要条件为：

对于任意的 $i$ 都有：

$s_{n-1}{s}_{n-2}\dots s_{i+1}{d}_i{d}_{i-1}{d}_{i-2}\dots d_2{d}_1{d}_{i+1}$ 不等于 $r_{n-1}{r}_{n-2}\dots r_{i+1}{t}_i{t}_{i-1}{t}_{i-2}\dots t_2{t}_1{t}_{i+1}$。

立方体 MIN 网络

立方体网络的自路由标记推导：

$C_i$ 为第 $n-i$个蝶形排列( $i=1,2,\dots ,n$ ), $C_0$ 为完全混洗

考虑从 $S_{n-1}{S}_{n-2}\dots S_1{S}_0$ 到 $d_{n-1}{d}_{n-2}\dots d_1{d}_0$ 建立一条链路
经过第 0 级链路： $S_{n-1}{S}_{n-2}\dots S_1{S}_0\to S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}$
$S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}$ 作为第 0 级开关的输入，
$S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}\to S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}^{\prime }$$S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}^{\prime }$ 作为第 1 级链路的输入：$S_{n-2}{S}_{n-3}\dots S_1{S}_0{S}_{n-1}^{\prime }\to S_{n-1}^{\prime }{S}_{n-3}\dots S_1{S}_0{S}_{n-2}$
经过第1级开关： $S_{n-1}^{\prime }{S}_{n-3}\dots S_1{S}_0{S}_{n-2}\to S_{n-1}^{\prime }{S}_{n-3}\dots S_1{S}_0{S}_{n-2}^{\prime }$
经过第2级链路： $S_{n-1}^{\prime }{S}_{n-3}\dots S_1{S}_0{S}_{n-2}^{\prime }\to S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_1{S}_0{S}_{n-3}$
经过第2级开关： $S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_1{S}_0{S}_{n-3}\to S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_1{S}_0{S}_{n-3}^{\prime }$
类似的第 $i$ 级开关： $S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_{n-i}^{\prime }{S}_{n-i-2}\dots S_1{S}_0{S}_{n-i-1}\to S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_{n-i}^{\prime }{S}_{n-i-2}\dots S_1{S}_0{S}_{n-i-1}^{\prime }$
从而第n-1级开关输出为 $S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_1^{\prime }{S}_0^{\prime }$
最后1级连伟恒等排列： $S_{n-1}^{\prime }{S}_{n-2}^{\prime }\dots S_1^{\prime }{S}_0^{\prime }=d_{n-1}{d}_{n-2}\dots d_1{d}_0$
所以 $S_i^{\prime }=d_i$
所以第i级开关输出为 $d_{n-1}{d}_{n-2}\dots d_{n-i}{S}_{n-i-2}\dots S_1{S}_0{d}_{n-i-1}^{\prime }$
在立方网络中，第 $i$ 级开关最低有效位为 $n-i-1$，并最终映射到目标地址的 $n-i-1$ 位，所以 $t_i=d_{n-i-1}(0\le i\le n-1)$

XY 多播路由模式

思路：每送完一个节点，将该节点从目的节点中去除。先沿着 X 轴从最左往最右送，到达每一个当前最左 X 后再沿着 Y 轴先上再下送。

目的节点集 $D^{{}^{\prime }}$，本地址 $(x,y)$

1. 若 x > m i n { x i ∣ ( x i , y i ) ∈ D ′ } x > min \{ x_i|(x_i,y_i)∈D^{'} \} x>min{xi​∣(xi​,yi​)∈D′} 则把消息和列表送到节点 $(x-1,y)$；若 x < m a x { x i ∣ ( x i , y i ) ∈ D ’ } x<max\{x_i|(x_i,y_i)∈D^{’}\} x<max{xi​∣(xi​,yi​)∈D’} 则把消息和列表送到节点 $(x+1,y)$。
2. 若 x ∈ { x i ∣ ( x i , y i ) ∈ D ′ } x∈\{x_i|(x_i,y_i)∈D^{'}\} x∈{xi​∣(xi​,yi​)∈D′}，判断 $y$ 的大小，若 y > m i n { y i ∣ ( x i , y i ) ∈ D ′ } y>min\{y_i|(x_i,y_i)∈D^{'}\} y>min{yi​∣(xi​,yi​)∈D′} 则把消息和列表送到 $(x,y-1)$，若 y < m a x { y i ∣ ( x i , y i ) ∈ D ′ } y<max\{y_i|(x_i,y_i)∈D^{'}\} y<max{yi​∣(xi​,yi​)∈D′}，则把消息和列表送到 $(x,y+1)$。
3. 若 $(x,y)\in D^{{}^{\prime }}$， $D^{{}^{\prime }}\leftarrow D^{{}^{\prime }}-(x,y)$，并把消息送到本地节点。

Chap4 对称多处理机系统

SMP 的特点

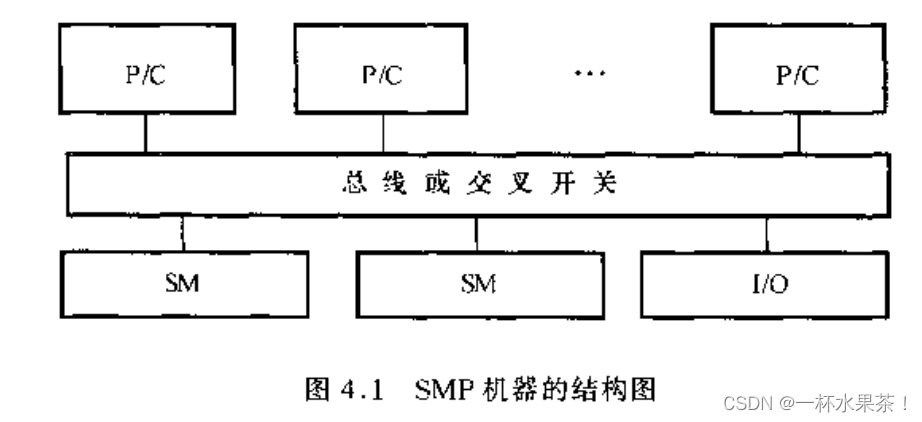
• 对称性
• 单一物理地址空间
• 高速缓存及其一致性
• 低通信延迟

扩展 SMP

前三种是对称的，第四种不是。

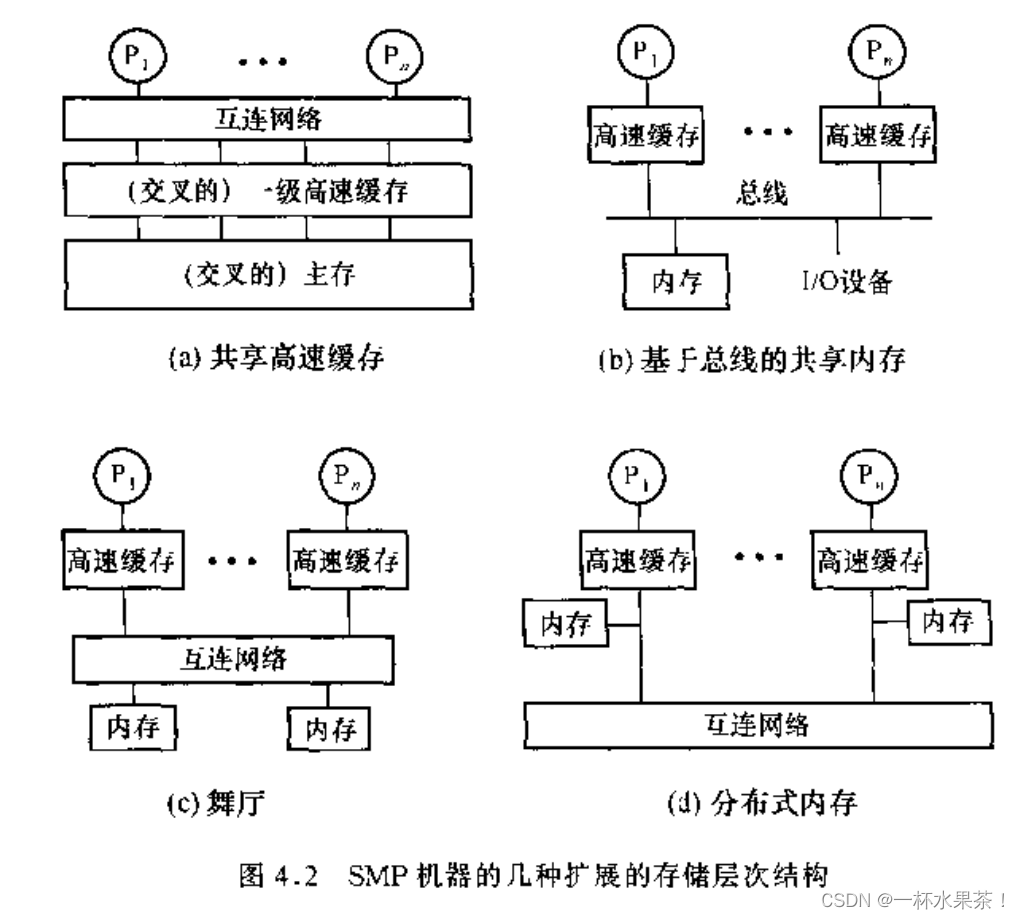
除了共享高速缓存，在所有结构中，每个处理器至少有一层高速缓存是私有的。

这就形成了高速缓存一致性问题。

同一个内存块的拷贝可能同时出现在多个处理器的高速缓存中，多个处理器对这些拷贝的存取，可能使这些拷贝的内容不一致。

• 造成高速缓存一致性问题的主要原因

  • 由共享可写数据所造成的不一致

    

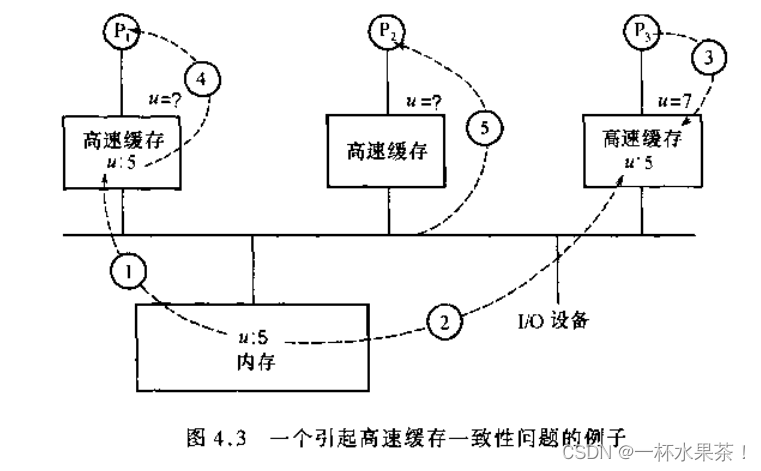
  • 由绕过高速缓存的 I/O 所造成的不一致

  • 由进程迁移所造成的不一致

高速缓存一致性

按照高速缓存的写策略的不同，有写直达 WT（Wrtite Through）和 写回 WB（Write Back）两种高速缓存。

• WT：一旦高速缓存中的一个字被修改，则在主存中立即修改。
• WB：当被修改的字从高速缓存中被替换或消除时，才真正修改主存。

总线侦听

基于总线的 SMP 通过共享总线连接微处理器（包括高速缓存）和共享存储器，因此利用总线的特性来实现高速缓存一致性。

总线连接多个设备，其上的每个设备都能侦听到总线上出现的事务。

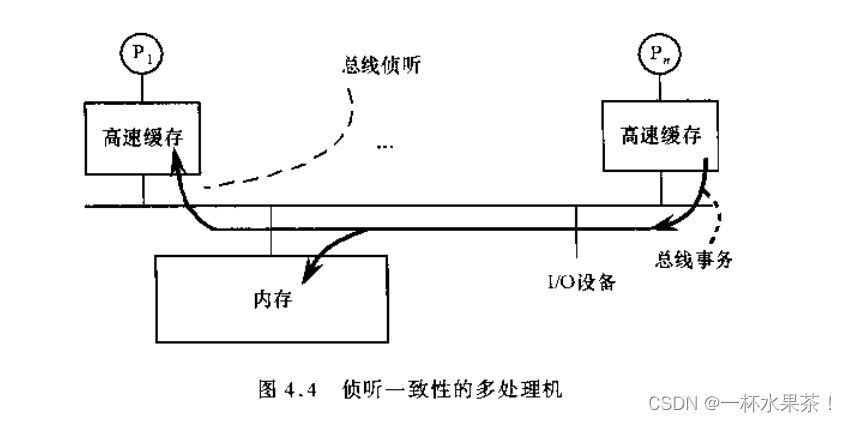
思想：

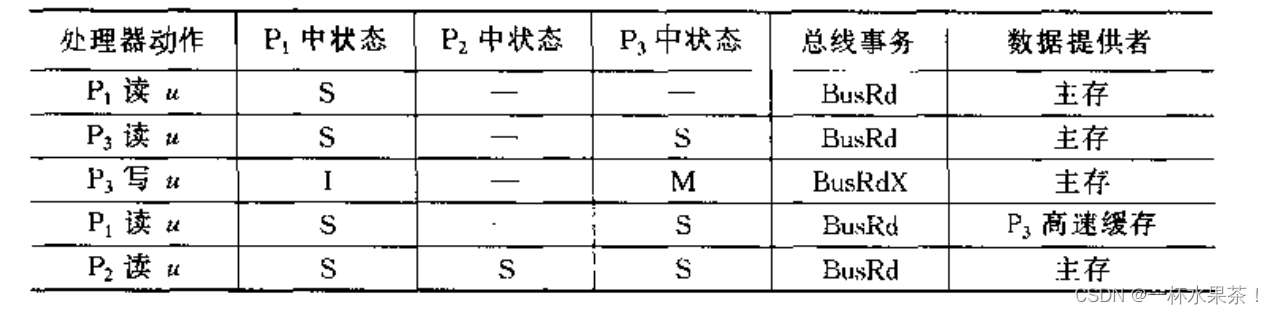
• 当一个处理器 $P_n$ 向内存发出一个内存读/写请求时，该处理器本地的高速缓存控制器检查自身的状态，并采取相应的动作。比如，读命中，则本地高速缓存直接响应；读缺失，则向总线发出存取内存的事务请求。
• 所有其他的高速缓存控制器 $P_1、\cdots 、P_{n-1}$ 都侦听总线上出现的事务，一旦事务与自己相关（自己的高速缓存有该事务请求内存块的一个拷贝），就执行相应的动作来保证高速缓存一致性。

总线序和程序序共同保证了高速缓存一致性。

单处理机中，当采用写直达且写不分配的高速缓存时，只需无效 I（Invalid）和有效 V（Valid）两个状态。

• 开始时，所有的块都是无效的。
• 当处理器发生一个读缺失时，高速缓存控制器产生一个总线事务从内存中读入该块，并将该块置为有效；
• 当处理器执行写操作时，高速缓存控制器产生一个总线事务去更新内存，如果所写的块在高速缓存中，且处于有效状态的话，则也更新高速缓存中块的内容，但不改变该块的状态。
• 当高速缓存中的一个块被替换出去时，将该块置为无效。

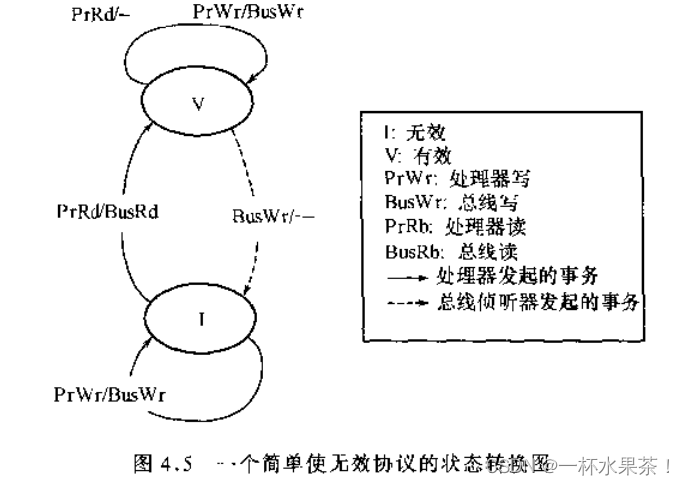
• V， PrRd/-：Valid，所以读命中。不触发总线事件，仍然 Valid。
• V， PrWr/BusWr：Valid，写命中。写直达，故既要写该数据块拷贝，又要写 Mem。需要总线 Invalid 其他数据块拷贝（Cache），即其他相应块会经历 V， BusWr/- -> I。
• V， BusWr/-：Valid，响应其他拷贝块发起的 BusWr，要 Invalid 自己相应的拷贝块变为 I。
• I， PrRd/BusRd：Invalid，所以读不命中。触发 BusRd，从 Mem 中读进最新的到该块，变为 Valid。
• I， PrWr/BusWr：要修改自己的 Cache 时，发现被 Invalid 了。但是，没关系，自己现在更新了，是最新的，故要通过 Bus Invalid 掉其他 Cache，再写到 Mem。

多处理机系统中，一个内存块在每个处理器的高速缓存中都有一个状态，所有的这些状态都按照状态转换图来转换。

侦听协议

两种设计选择：

• 是写直达，还是写回；
• 是写无效 WI（Write-Invalidate），还是写更新 WU（Write-Update）。

写直达，主存总与高速缓存中最新值一致，每次写操作都需要更新主存，从而需要额外的总线周期；

写回，主存的更新在发生替换时才进行，只需占有较少的总线周期，但存在短暂不一致。

【总结】写回方式中尽量延迟写直达中对主存的更新，而且可以快速实现写命中，故在存储器总线结构上采用写回高速缓存更经济。

写无效，本地高速缓存中数据被更新后，使所有其他高速缓存中的相应数据拷贝无效，那么处理器发出的对内存块的写操作就不会引起总线上的任何通信。

写更新，广播修改后的数据，以更新所有的高速缓存中的相应数据拷贝，那么当拥有该块拷贝的处理器接下来存取这个新数据时，存取延迟就很小。

【总结】由于一个总线事务就能更新所有拥有该块的高速缓存中内容，所以如果该块有多个共享者，就能极大地节约总线带宽。

MSI

MSI 协议比较简单，它定义了三个状态：

1. Modified：表示数据已经修改，和内存里不一致
2. Shared：数据和内存一致，可以有一到多个缓存同时处在 Shared 状态
3. Invalid：不在缓存中

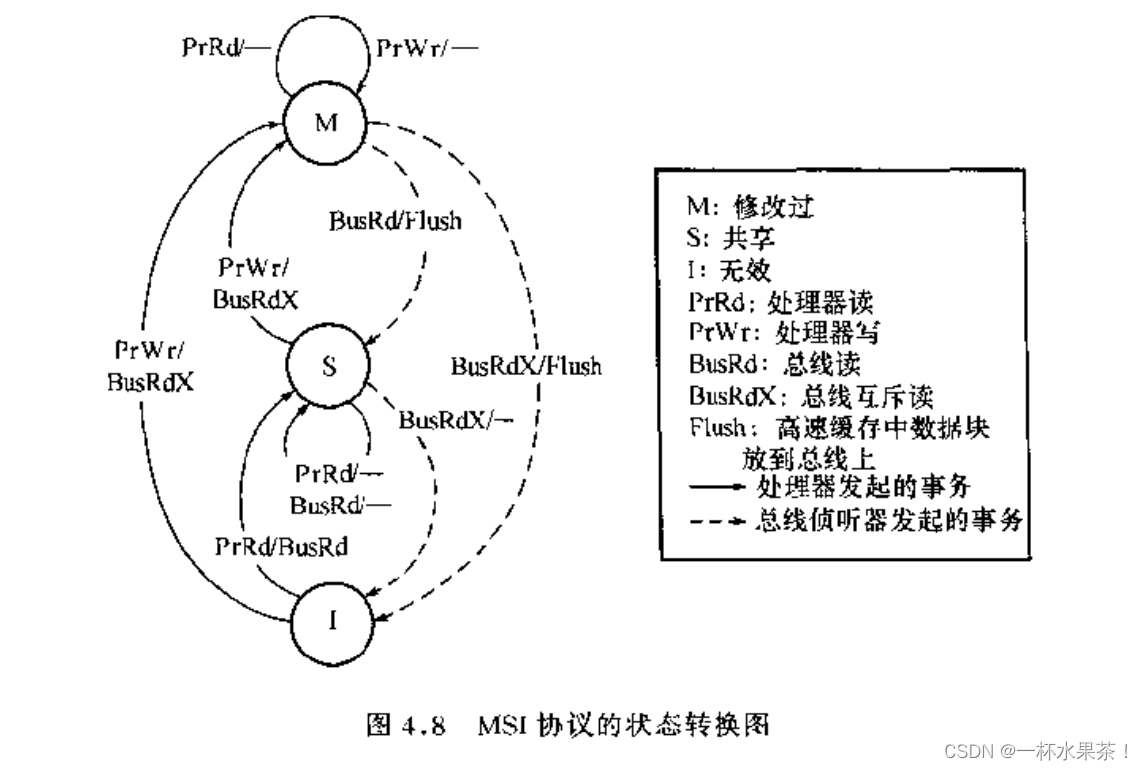
当 Read hit 的时候，状态不变。

当 Read miss 的时候，检查其他缓存的状态，

• 如果都是 Invalid，就从内存里读取，然后进入 Shared 状态。
• 如果有 Shared，就从其他缓存处读取。
• 如果有 Dirty，那就要把其他缓存的数据写入内存和本地缓存，然后进入 Shared 状态。

当 Write hit 的时候，

• 如果现在是 Shared 状态，则要让其他的 Shared 缓存进入 Invalid 状态，然后更新数据，进入 Modified 状态。
• 如果是 Modified 状态，那就修改数据，状态保持不变。

当 Write miss 的时候，

• 如果有其他缓存处于 Modified/Shared 状态，那就从其他缓存处读取数据，并让其他缓存进入 Invalid 状态，然后修改本地数据，进入 Modified 状态。
• 如果所有缓存都是 Invalid 状态，那就从内存读入，然后修改缓存数据，进入 Modified 状态。

MESI

MESI 协议定义了四种状态：

1. Modified：数据与内存不一致，并且只有一个缓存有数据
2. Exclusive：数据与内存一致，并且只有一个缓存有数据
3. Shared：数据与内存一致，可以有多个缓存同时有数据
4. Invalid：不在缓存中

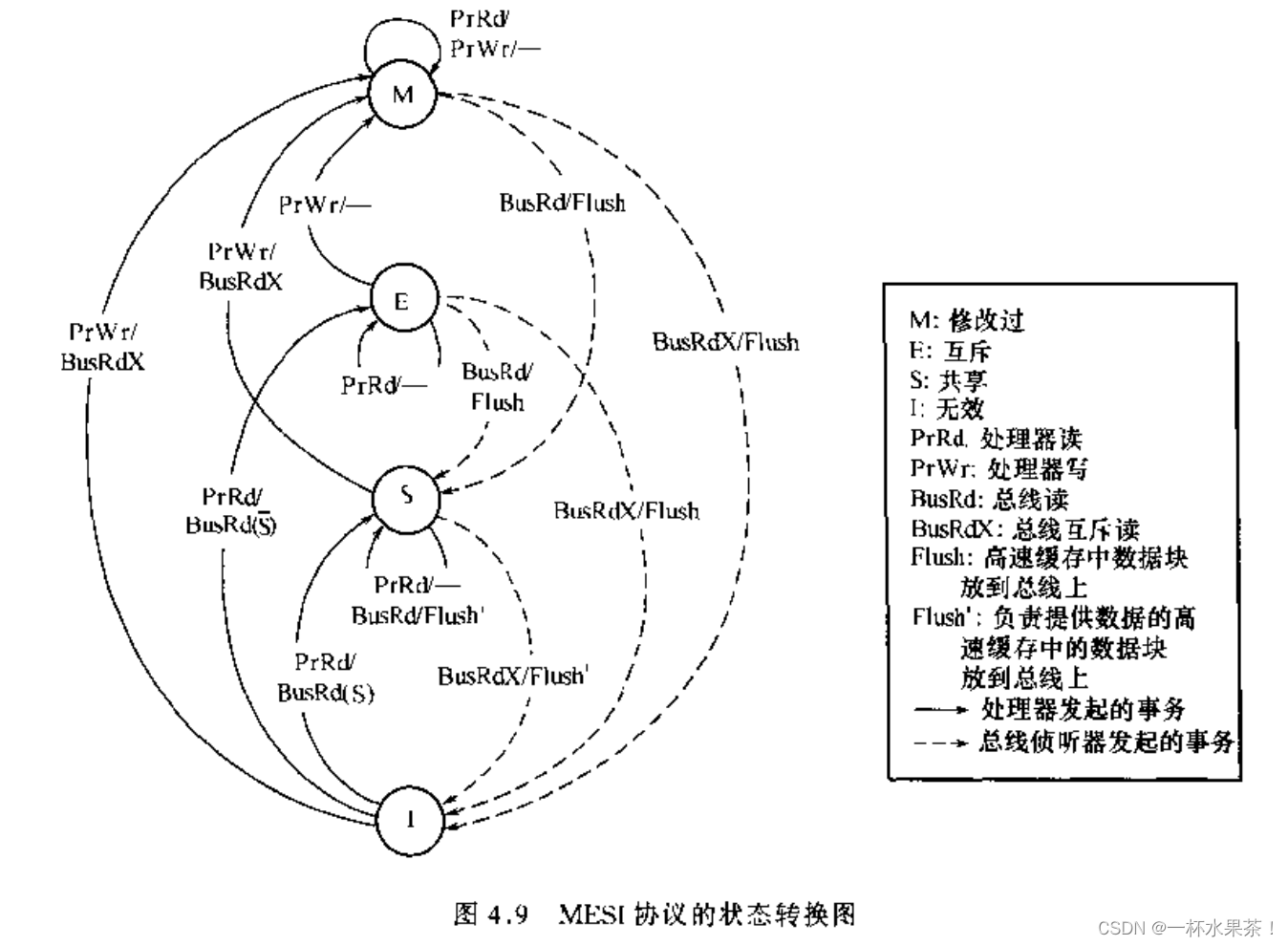
当 Read hit 的时候，状态不变。

当 Read miss 的时候，首先会检查其他缓存的状态，

• 如果有数据，就从其他缓存读取数据，并且都进入 Shared 状态；
• 如果其他缓存处于 Modified 状态，还需要把数据写入内存；
• 如果其他缓存都没有数据，就从内存里读取，然后进入 Exclusive 状态。

当 Write hit 的时候，进入 Modified 状态，同时让其他缓存进入 Invalid 状态。

当 Write miss 的时候，检查其他缓存的状态，

• 如果有数据，就从其他缓存读取，否则从内存读取。
• 然后，其他缓存都进入 Invalid 状态，本地缓存更新数据，进入 Modified 状态。

注意，Shared 状态不一定表示只有一个缓存有数据：比如本来有两个缓存都是 Shared 状态，然后其中一个因为缓存替换变成了 Invalid，那么另一个是不会受到通知变成 Exclusive 的。Exclusive 的设置是为了减少一些总线请求，比如当数据只有一个核心访问的时候，只有第一次 Read miss 会发送总线请求，之后一直在 Exclusive/Modified 状态中，不需要发送总线请求。

Dragon

Dragon 协议是一个基于更新的协议，意味着写入缓存的时候，会把更新的数据同步到拥有这个缓存行的其他缓存块。

基于更新的协议（例如 Dragon 协议）在写入缓存块之后由其他处理器进行多次读取时会高效执行，因为更新的缓存块很容易在与所有处理器关联的缓存中使用。

它定义了四个状态：

1. Exclusive clean(E)：独占，并且数据和内存一致
2. Shared clean(Sc)：数据同时存在多个缓存中，并且自己不是最后一个写入该缓存数据的
3. Shared modified(Sm)：数据同时存在多个缓存中，并且自己是最后一个写入该缓存数据的
4. Modify(M)：独占，并且数据和内存不一致

可以看到，E 和 M 都是独占的，如果出现了多个缓存有同一个缓存行，那就是若干个 Sc 和一个 Sm。

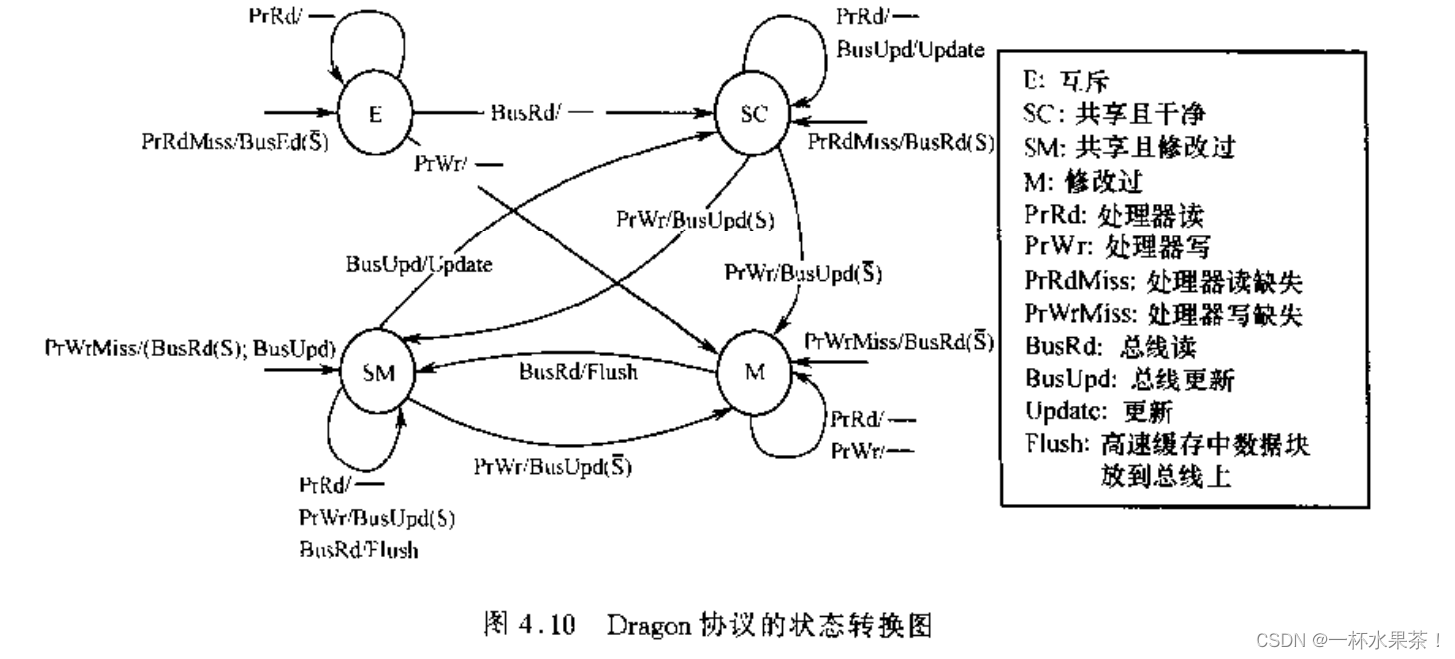
当 Read miss 的时候，在总线上检查是否有缓存已经有这个缓存行的数据，

• 如果没有，则从内存读取并转到 Exclusive clean 状态；
• 如果已经在其他缓存中，则从其他缓存读取，将其他缓存转移到 Shared clean/Shared modified 状态，然后该缓存转移到 Shared clean 状态。

当 Write miss 的时候，同样检查其他缓存的状态，

• 如果是第一个访问的，就从内存读取，更新数据，然后转到 Modify 状态；
• 如果不是第一个访问的，就进入 Shared modified 状态，并且让原来 Shared modified 的缓存进入 Shared clean 状态。

当 Write hit 的时候，

• 如果状态是 Shared modified，这时候需要通知其他缓存更新数据；
• 如果状态是 Shared clean，则要通知其他缓存更新数据的同时，让原来 Shared modified 的缓存进入 Shared clean 状态；
• 如果状态是 Exclusive clean，则进入 Modify 状态。

在这里，Shared modified 的缓存负责在换出的时候，写入数据到内存中。

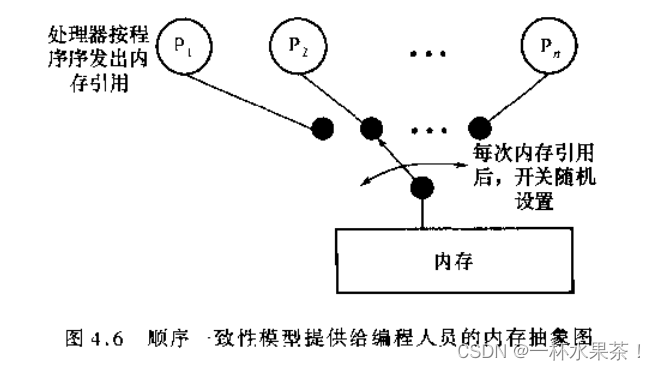
顺序一致性

顺序一致性是对所有的读/写操作的一致性要求；

高速缓存一致性是对同一个内存位置的读/写操作的一致性要求。

Chap6 机群系统