DFS之搜索顺序——AcWing 1116. 马走日

DFS之搜索顺序

定义

DFS之搜索顺序是指在执行深度优先搜索时，遍历图或树中节点的策略。具体而言，DFS会沿着一条路径深入到底，当无法继续深入时回溯，然后选择另一条未探索的路径继续深入。搜索顺序直接影响到搜索效率和剪枝的可能性，合理的顺序可以减少搜索空间，加速找到解的过程。

运用情况

路径查找：如寻找图中的最短路径或特定路径。
图的遍历：全面探索图的所有节点，常用于判断连通性、强连通分量等。
回溯问题：如八皇后、生成括号组合等，DFS自然地支持解决方案的生成与回溯。
游戏策略：如解决迷宫问题、井字游戏的胜利条件检查等。
树的遍历：前序、中序、后序遍历等，虽然是树的特例，但也是DFS的应用。

注意事项

避免循环：通过标记已访问节点来避免重复访问，防止无限循环。
剪枝：合理安排搜索顺序，尽早排除不可能产生解的分支，减少无效计算。
栈的使用：DFS通常与栈数据结构紧密相关，需注意栈的大小限制，避免栈溢出。
记忆化：对于有重叠子问题的情形，可以使用记忆化技术存储中间结果，避免重复计算。
起始节点选择：在多源或多连通分量的场景下，需要从每个未访问的节点开始执行DFS。

解题思路

初始化：标记所有节点为未访问，设置起始节点。
选择路径：从起始节点出发，选择一个未访问的邻接节点作为下一步探索的目标。
递归/迭代深入：递归或使用栈模拟递归，深入探索选定的路径，同时标记访问过的节点。
回溯：当路径无法继续深入时，返回上一层节点，尝试探索该节点的其他未访问邻居。
结束条件：当所有可达节点都被访问过，或找到所需的解时，DFS结束。
优化：根据问题特性设计搜索顺序，比如在某些问题中按某种排序规则访问邻接点可以减少搜索空间。

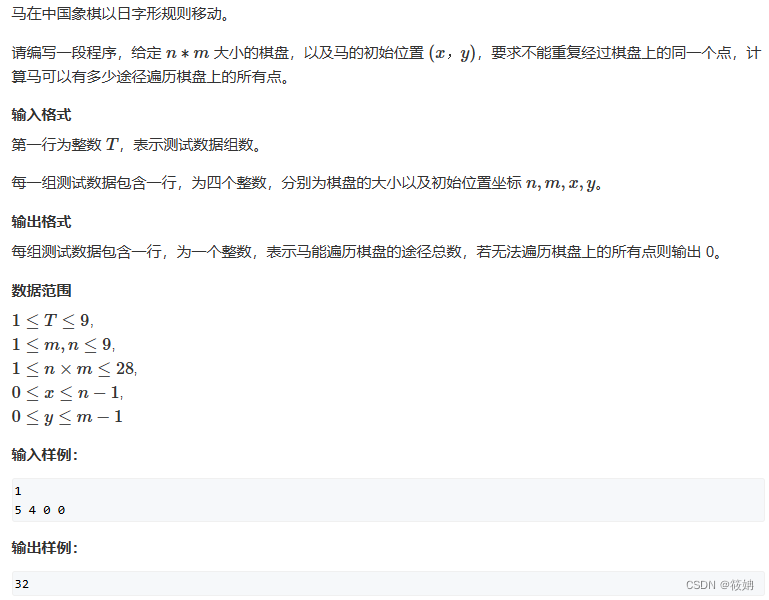
AcWing 1116. 马走日

题目描述

AcWing 1116. 马走日 - AcWing

运行代码

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10;int n, m;
bool st[N][N];
int ans;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};void dfs(int x, int y, int cnt)
{if (cnt == n * m){ans ++ ;return;}st[x][y] = true;for (int i = 0; i < 8; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m) continue;if (st[a][b]) continue;dfs(a, b, cnt + 1);}st[x][y] = false;
}int main()
{int T;scanf("%d", &T);while (T -- ){int x, y;scanf("%d%d%d%d", &n, &m, &x, &y);memset(st, 0, sizeof st);ans = 0;dfs(x, y, 1);printf("%d\n", ans);}return 0;
}

代码思路

定义变量：
- n 和 m 分别代表网格的行数和列数。
- st[N][N] 是一个布尔型数组，用来标记每个网格格子是否已被访问过。
- ans 记录可行的方案数。
- dx[] 和 dy[] 分别存储了马在八个可能移动方向上的横纵坐标变化值。
主函数main()：
- 首先读取测试用例数量 T。
- 然后对于每一个测试用例：
  - 读取网格大小 n 和 m，以及起始位置 x, y。
  - 清零状态数组 st 和答案计数器 ans。
  - 调用深度优先搜索函数 dfs()，传入起始位置和初始计步数 1。
  - 输出最终得到的可行方案数 ans。
深度优先搜索函数dfs(int x, int y, int cnt)：
- 基线条件：如果当前已经访问了所有的n*m个格子（即 cnt == n * m），说明找到了一种合法的走法，因此答案加一，然后返回。
- 状态标记：标记当前位置 (x, y) 为已访问。
- 探索相邻节点：对于马可以走的八个方向，依次检查是否越界以及是否已经访问过。如果没有，则继续以当前位置为起点进行深度优先搜索，同时计步数加一。
- 回溯：在对一个方向的探索结束后，需要将当前位置的状态重置为未访问，以便探索其他路径。

改进思路

剪枝策略：位置合法性检查提前：在进入dfs递归之前，预先判断当前位置(x, y)是否可能达到目标。例如，当剩余步数(cnt)超过剩余未访问格子数时，无需继续搜索，直接返回。避免重复路径：记录并检查已访问路径，如果发现当前路径与之前的某条路径重复（可以通过记录访问顺序实现），则直接返回，避免循环搜索。
记忆化搜索：对于较大的n和m，可以采用记忆化搜索减少重复计算。使用一个三维数组dp[x][y][cnt]记录从位置(x, y)出发，已经走了cnt步时的方案数。在进行dfs之前先检查dp[x][y][cnt]是否已有计算结果，若有则直接使用，避免重复计算。
双向BFS或A*搜索：
- 当寻找特定目标或优化搜索速度时，考虑使用双向BFS或启发式搜索如A*算法。双向BFS从起点和终点同时开始搜索，当两个搜索前线相遇时即可停止，这通常能更快找到解。
- A*算法利用启发式信息估计从当前节点到目标节点的成本，有助于在搜索过程中选择更优路径，减少不必要的探索。
并行处理：对于非常大的问题，可以考虑使用并行计算框架（如OpenMP、C++17的并行算法库等）来并行执行多个起始点的DFS或BFS，加速搜索过程。
输入输出优化：使用更快的输入输出方法（如缓冲读写）减少IO时间，尤其是在处理大量测试用例时，这能显著提升整体运行效率。
代码优化：宏观上看，可以考虑将一些常量（如方向数组的长度8）提取为常量定义，提高代码可读性和维护性。微观上，减少不必要的变量创建和销毁，优化循环和递归调用，都有助于提高程序运行效率。