【Python机器学习】模型评估与改进—

1、错误类型

2、不平衡数据集

3、混淆矩阵

与精度的关系。

准确率、召回率与f-分数

分类报告

4、考虑不确定性

5、准确率-召回率曲线

6、受试者工作特征（ROC）与AUC

二分类可能是实践中最常见的机器学习应用，也是概念最简单的应用。但是即使是评估这个简单的任务也仍有一些注意事项。对于二分类问题，我们通常会说正类和反类，而正类使我们要寻找的类。

1、错误类型

通常来说，精度并不能很好的度量预测性能，因为我们所犯错误的数量并不包含我们感兴趣的所有信息。想象一个应用，利用自动化测试来筛查癌症的早期发现。如果测试结果为阴性，那么认为患者是健康的，如果测试结果为阳性，那么患者则需要接收额外的筛查。这里我们将阳性结果称为正类，阴性测试称为反类。我们不能假设模型永远是完美的，它也会犯错。对于任何应用而言，我们都需要问问自己，这些错误在现实世界中可能有什么后果。

一种可能的错误是健康的患者被诊断为阳性，导致需要进行额外的测试。这会给患者带来一些额外的支出和不便。错误的阳性预测被称为假正例。另一种可能的错误是患病的人被诊断为阴性，因而不会接受进一步的检查，可能导致严重的健康问题，这种错误的类型被叫做假反例，也叫做第二类错误。

2、不平衡数据集

如果在两个类别中，一个类别的出现次数比另一个多得多，那么错误类型将发挥重要作用，这在实践中非常常见。一个很好的例子是点击预测，其中每个数据点表示一个印象，即向用户展示的一个物项。这个物项可能是广告、故事，或者在社媒上关注的用户。目标是预测用户是否会点击看到的某个特定物项。用户对互联网上显示的大多数内容都不会点击。你可能向用户展示100个广告，用户才点击一次，这样就会得到一个数据集，其中每99个“未点击”的数据点才有一个“已点击”的数据点。换句话说，00%的样本属于“未点击”类别，这种一个类别比另一个类别出现的次数多很多的数据集，通常叫做不平衡数据集或者具有不平衡类别的数据集。在实际中，不平衡数据才是常态。

如果在上述的数据集上构造一个点击预测任务重精度达到99%的分类器，只要预测“未点击”，就可以达到99%的精度，但这样的精度无法帮助我们区分不变的“未点击”模型与潜在的优秀模型。

为了便于说明，我们将digits数据集中的数字9与其他九个类别加以区分，从而创建一个9:1的不平衡数据集，并使用DummyClassifier来始终预测多数类，以查看精度提供的信息量有多么少：

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.dummy import DummyClassifier
import numpy as npdisits=load_digits()
y=disits.target==9X_train,X_test,y_train,y_test=train_test_split(disits.data,y,random_state=0)
dummy_majority=DummyClassifier(strategy='most_frequent').fit(X_train,y_train)
pred_most_frequent=dummy_majority.predict(X_test)
print('标签：{}'.format(np.unique(pred_most_frequent)))
print('测试集精度:{:.2f}'.format(dummy_majority.score(X_test,y_test)))

我们得到了接近90%的精度，却没有学到任何内容。这个结果可能看起来相当好，但根据具体问题，也可能是仅预测了一个类别，我们将这个结果与使用一个真实分类器的结果进行对比：

tree=DecisionTreeClassifier(max_depth=2).fit(X_train,y_train)
pred_tree=tree.predict(X_test)
print('测试集精度:{:.2f}'.format(tree.score(X_test,y_test)))

从精度上来看，DecisionTreeClassifier仅比常数预测稍微好一点，这可能表示我们使用DecisionTreeClassifier的方法有误，也可能是因为精度实际上在这里不是一个很好的变量。

为了便于对比，我们再评估两个分类器，LogisticRegression与默认的DummyClassifier，其中后者进行随机预测，但预测类别的臂力与训练集中的比例相同：

dummy=DummyClassifier().fit(X_train,y_train)
pred_dummy=dummy.predict(X_test)
print('DummyClassifier测试集精度:{:.2f}'.format(dummy.score(X_test,y_test)))logreg=LogisticRegression().fit(X_train,y_train)
pred_logreg=logreg.predict(X_test)
print('LogisticRegression测试集精度:{:.2f}'.format(logreg.score(X_test,y_test)))

可以看到，产生随机输出的虚拟分类器是所有分类器中最差的，而LogisticRegression则给出了相当好的结果。但是，即使是随机分类器也得到了超过90%的精度。这样很难判断哪些结果是真正有帮助的。这里的问题在于，要想对这种不平衡数据的预测性能进行量化，精度并不是一种合适的度量。

我们希望有一个指标告诉我们，一个模型比最常见预测或随机预测要好多少。如果用一个指标来评估模型，那么这个指标应该能够淘汰这些无意义的预测。

3、混淆矩阵

对于二分类问题的评估结果，一种最全面的表示方法是使用混淆矩阵。我们利用confusion_matrix函数来检查上面的LogisticRegression的预测结果：

from sklearn.metrics import confusion_matrix
confusion=confusion_matrix(y_test,pred_logreg)
print('混淆矩阵：\n{}'.format(confusion))

confusion_matrix输出的是一个2*2数组，其中行对应真实的类别，列对应预测的类别。数组中每个元素给出属于该行对应类别（这里是“9”和“非9”）的样本被分类到该列对应类别中的数量。

如图说明：

mglearn.plots.plot_confusion_matrix_illustration()
plt.show()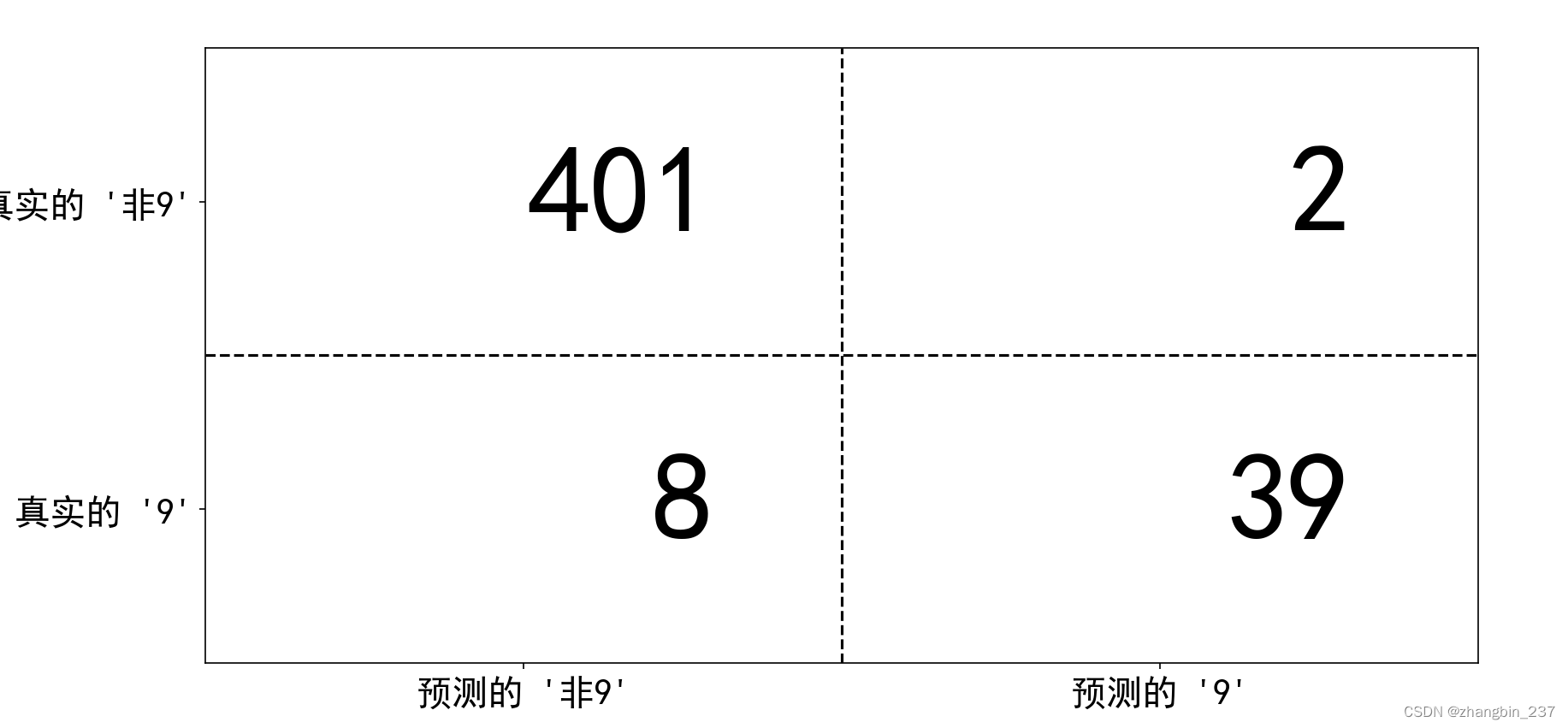

如果我们将‘9’作为正类，那么就可以将混淆矩阵的元素与前面介绍过的假正例和假反例两个术语联系起来，为了使图像更完整，我们将正类中正确分类的样本称为真正例，将反类中正确分类的样本称为真反例。这些属于通常缩写为FP（假正例）、FN（假反例）、TP（真正例）、TN（真反例），这样就得到下图对混淆矩阵的解释：

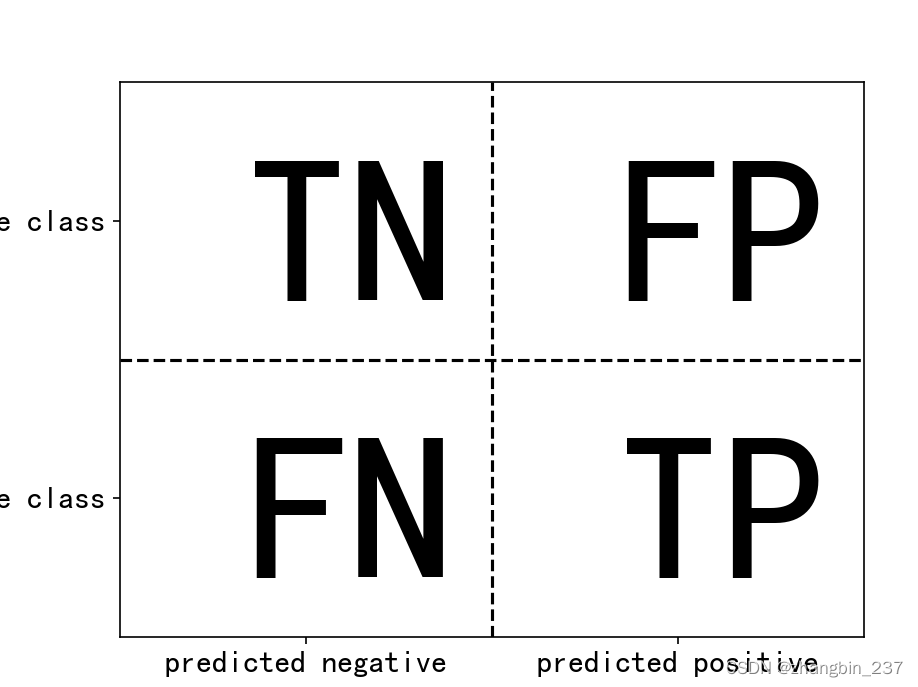
下面用混淆矩阵来比较前面拟合过的模型（两个虚拟模型、决策树、Logistic回归）

print('始终预测多数类的混淆矩阵：\n{}\n'.format(confusion_matrix(y_test,pred_most_frequent)))
print('DummyClassifier混淆矩阵：\n{}\n'.format(confusion_matrix(y_test,pred_dummy)))
print('决策树的混淆矩阵：\n{}\n'.format(confusion_matrix(y_test,pred_tree)))
print('Logistic回归的混淆矩阵：\n{}\n'.format(confusion_matrix(y_test,pred_logreg)))

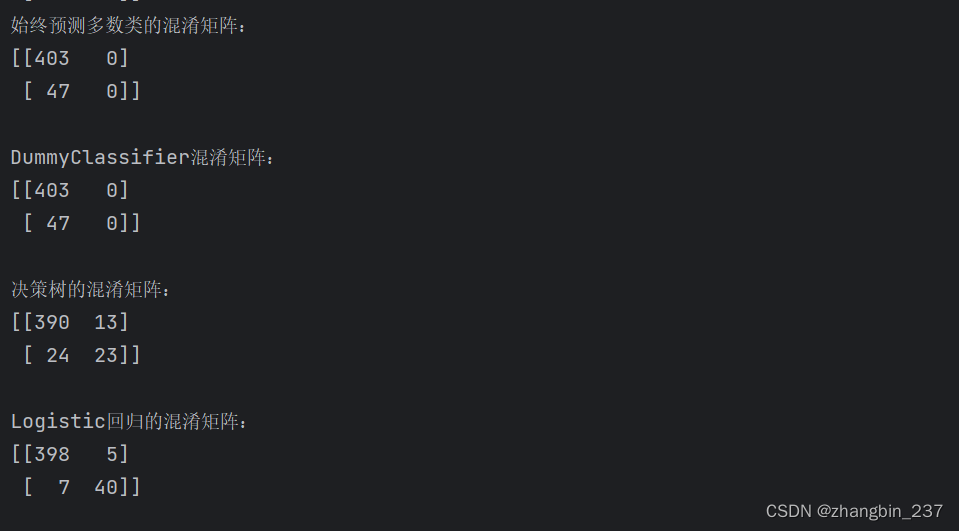
可以看到，很明显的多数类预测和pred_dummy很有问题，他们总是预测同一个类别。

Logistic回归在各方面都比较好：它的真正例和真反例的数量更多，而假正例和假反例的数量更少。从这个对比中明显看出，只有决策树和Logistic回归给出了合理的结果，并且Logistic回归的效果全面好于决策树。但是，检查整个混淆矩阵有点麻烦，虽然我们通过观察矩阵的各个方面得到了很多深入见解，但这个过程是人工完成的，也是非常定性的。

有几种方法可以总结混淆矩阵中包含的信息，之后展示。

与精度的关系。

这是一种总结混淆矩阵的方法——计算精度，其公式表达：Accuracy=(TP+TN)/(TP+TN+FP+FN)，换句话说，精度是正确预测的数量（TP和TN）除以所有样本的数量（混淆矩阵中所有元素的和）

准确率、召回率与f-分数

总结混淆矩阵还有几种方法，其中最常见的就是准确率和召回率。

准确率度量的是被预测为正例的样本中有多少是真正的正例：Precision=TP/(TP+FP)

如果目标是限制假正例的数量，那么可以使用准确率作为性能指标。准确率也被称为阳性预测值。

另一方面，召回率度量的是正类样本中有多少样本中被预测为正例：Recall=TP/(TP+FN)

如果我们需要找出所有的正类样本，即避免假反例是很重要的情况下，那么可以使用召回率作为性能指标。召回率的其他名称有灵敏度、命中率、和真正例率。

在优化召回率与优化准确率之间需要折中。如果预测所有样本都属于正类，那么可以轻松得到完美的召回率（没有假反例），也没有真反例。但是，将所有样本都预测为正类，会得到许多假正例，因此准确率会很低。与之相反，如果你的模型只将一个最确定的数据点预测为正类，其他点都预测为反类，那么准确率会很完美，但是召回率会很差。

虽然准确率和召回率是非常重要的度量，但是仅查看二者之一无法提供完整的图景。将两种度量进行汇总的一种方法是f-分数，或f-度量，它是准确率与召回率的调和平均：F=2*(Precision*Recall)/(Precision+Recall)。这一特定变体也被称为 $f_{1}$ 分数。由于同时考虑了准确率和召回率，所以它对于不平衡的二分类数据集来说是一种比精度更好的度量。

print('f1 score most frequent:{:.2f}'.format(f1_score(y_test,pred_most_frequent)))
print('f1 score dummy:{:.2f}'.format(f1_score(y_test,pred_dummy)))
print('f1 score 决策树:{:.2f}'.format(f1_score(y_test,pred_tree)))
print('f1 score Logistic回归:{:.2f}'.format(f1_score(y_test,pred_logreg)))

这里可以注意到两件事：

1、我们从most_frequent的预测中得到一条错误信息，因为预测的正类数量为0（使得f-分数的分母为0）；

2、我们可以看到虚拟预测与决策树预测之间有很大的区别，而仅观察精度时二者区别并不明显。

利用f-分数进行评估，我们再次用一个数字总结了预测性能。打码机f-分数似乎比精度更加符合我们对好模型的直觉，但是f-分数的一个缺点是比精度更难理解。

分类报告

如果我们想要对准确率、召回率和 $f_{1}$ 分数做一个更全面的总结，可以使用classification_report这个很方便的函数，它可以同时计算这三个值，并以美观的格式打印出来：

print(classification_report(y_test,pred_most_frequent,target_names=['非9','9']))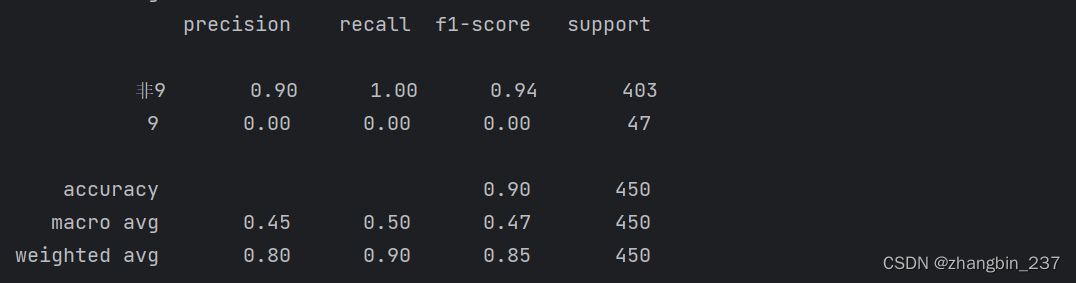

classification_report函数为每个类（这里是True和False）生成一行，并给出以该类别作为正类的准确率、召回率、f-分数。前面我们假设较少的“9”类为正类。如果将正类改为“非9”，我们可以从classification_report的输出结果中看出，利用most_frequent模型得到的f-分数为0.94。此外，对于“非9”类别，召回率是1，因为我们将所有样本都分类为“非9”。f-分数旁边的最后一列给出了每个类别的支持率（support），它表示的是这个类别中真实样本的数量。

分类报告的最后一行显示的是对应指标的加权平均。下面的两个报告，分别是虚拟分类器和Logistic回归的：

print('虚拟分类器',classification_report(y_test,pred_dummy,target_names=['非9','9']))
print('Logistic回归',classification_report(y_test,pred_logreg,target_names=['非9','9']))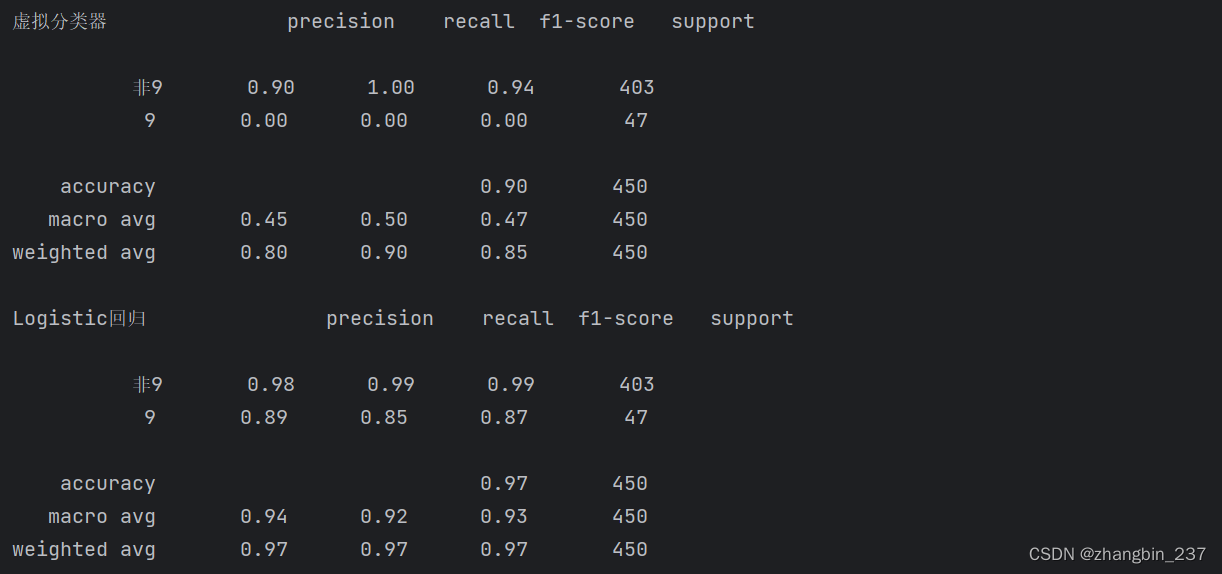

在查看报告时可以看到，虚拟模型与好模型之间的区别不再那么明显。选择哪个类作为正类对指标有很大影响。虽然以“9”类作为正类时虚拟分类的f-分数是0.1（对比Logistic回归的0.89），而以“非9”类作为正类的f-分数分别是0.91和0.99，两个结果看起来都很合理。不过同时查看所有数字可以给出非常准确的图像，我们可以清楚的看到Logistic回归模型的优势。

4、考虑不确定性

混淆矩阵和分类报告为一组特定的预测提供了非常详细的分析。但是，预测本身已经丢弃了模型汇总包含的大量信息。大多数分类器都提供了一个decision_function或predict_proba方法来评估预测的不确定度。预测可以被看做是以某个固定点作为decision_function或predict_proba输出的阈值——在二分类问题中，我们使用0作为决策函数的阈值，0.5作为predict_proba的阈值。

下面是一个不平衡二分类任务的示例，反类有400个点，而正类只有50个点。训练数据如下图左侧。我们在这个数据上训练一个核SVM模型，训练数据右侧的图像将决策函数值绘制为热图。我们可以子啊图像偏上的位置看到一个黑色圆圈，表示decision_function的阈值刚好问为0.在这个圆圈内的点将被划为正类，圆圈外的点将被划为反类：

import mglearn.plots
from sklearn.datasets import load_digits,make_blobs
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVCplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = FalseX,y=make_blobs(n_samples=(400,50),cluster_std=[7.0,2],random_state=22)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
svc=SVC(gamma=0.05).fit(X_train,y_train)mglearn.plots.plot_decision_threshold()
plt.show()

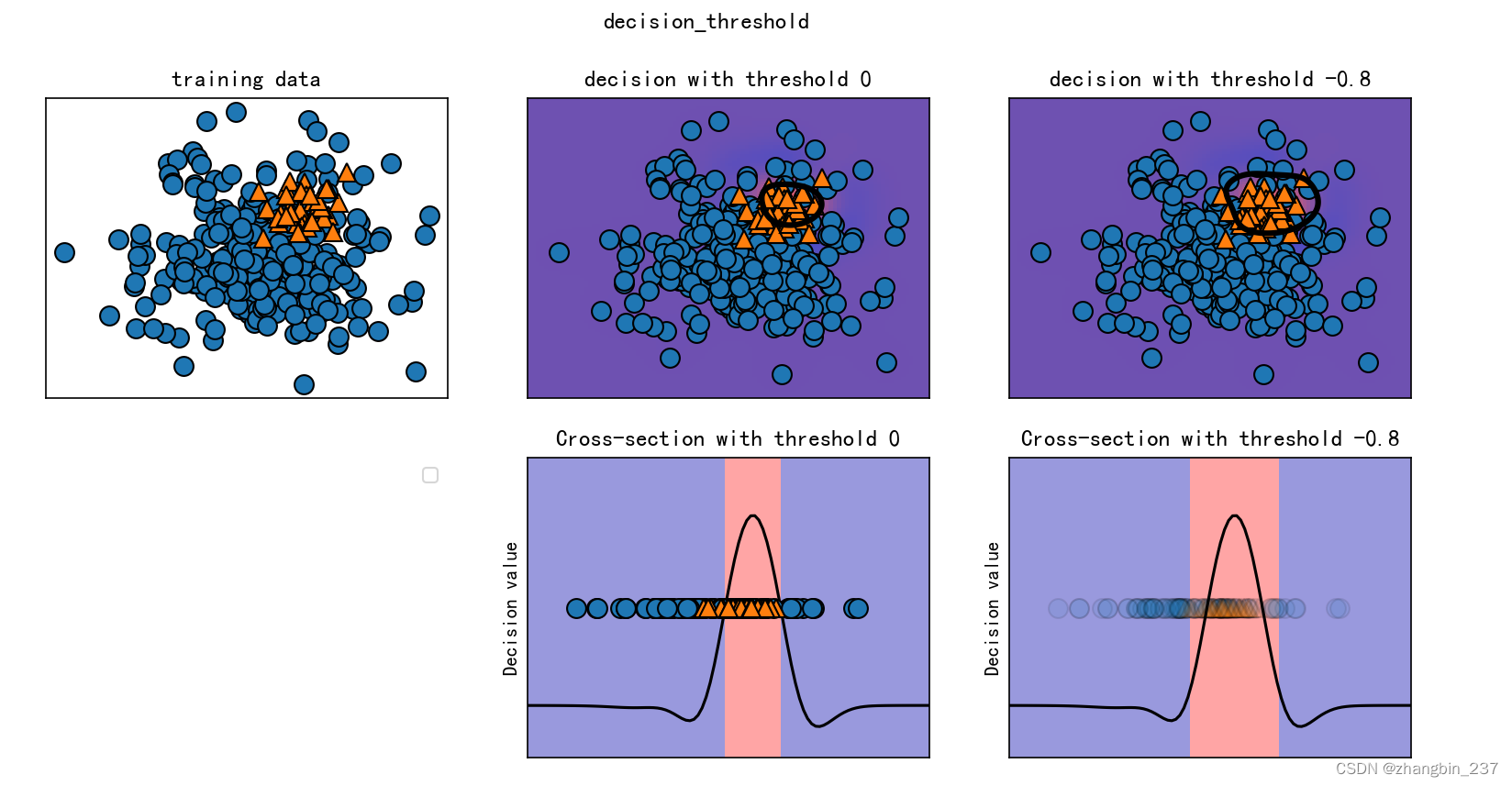
我们可以使用classification_report函数来评估两个类别的准确率与召回率：

print(classification_report(y_test,svc.predict(X_test)))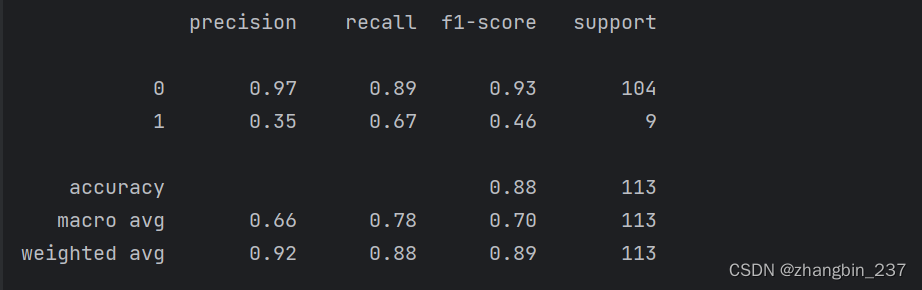

对于类别1，我们得到了一个相当低的准确率，而召回率则令人糊涂。由于类别0要大得多，所以分类器将重点放在类别0分类正确，而不是较小的类别1。

假设在我们的应用中，类别1具有高召回率更加重要，这意味着我们愿意冒险有更多的假正例，以换取更多的真正例。svc.predict生成的预测无法满足这个要求，但我们可以通过改变决策阈值不等于0来将预测重点放在使类别1的召回率更高。默认情况下，decision_function值大于0的点将被划分为1。我们希望将更多的点划分为1，所以需要减小阈值。

y_pred_lower_threshold=svc.decision_function(X_test)>-.8
print(classification_report(y_test,y_pred_lower_threshold))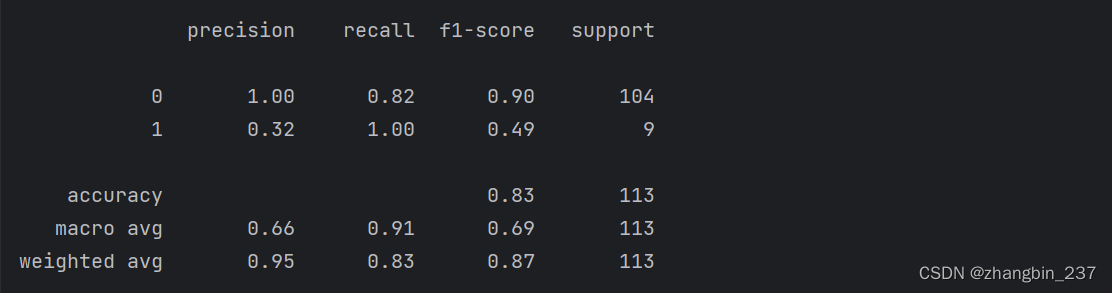

正如所料，类别1 的召回率增大，准确率减小。现在我们将更大的空间区域划分为类别1，正如上图右上图所示，如果认为准确率比召回率更重要，或者反过来，或者数据严重不平衡，那么改变决策阈值是得到更好结果的最简单方法。由于decision_function的取值可能在任意范围，所以很难提供关于如何选取阈值的经验法则。

对于实现了predict_proba方法的模型来说，选择阈值可能更简单，因为predict_proba的输出固定在0到1的范围内，表示的是概率。默认情况下，0.5的阈值表示，如果模型以超过50%的概率“确信”一个点属于正类，那么就将其划为正类。增大这个阈值意味着模型需要更加确信才能做出正类的判断。虽然使用概率可能比使用任意阈值更加直观，但并非所有模型都提供了不确定性的实际模型。这与校准的概念相关：校准模型是指能够为其不确定性提供准确度量的模型。

5、准确率-召回率曲线

之前说过，改变模型汇总用于分类决策的阈值，是一种调节给定分类器的准确率和召回率之间折中的方法。你可能希望仅遗漏不到10%的正类样本，即希望召回率能够达到90%。这一决策取决于应用，应该是由商业目标驱动的。一旦设定了一个具体目标，就可以适当地设定一个阈值，总是可以设置一个阈值来满足特定的目标，比如90%的召回率。难点在于开发一个模型，在满足这个阈值的同时仍具有合理的准确率——如果你将所有样本都划为正类，那么将会得到100%的召回率，但这个模型毫无用处。

对分类器设置要求（比如90%的召回率）通常被称为设置工作点。在业务中固定工作点通常有助于为客户或组织内的其他小组提供性能保证。

在开发新模型时，通常并不完全清楚工作点在哪里。因此，为了更好地理解模型问题，很有启发性的做法是，同时查看所有可能的阈值或准确率和召回率的所有可能折中。利用一种叫做准确率—召回率曲线的工具可以做到这一点。我们可以在scikit-learn模块中找到计算准确率—召回率曲线的函数。这个函数需要真实标签与预测的不确定度，后者由decision_function或predict_proba给出：

from sklearn.metrics import precision_recall_curve
precision,recall,thresholds=precision_recall_curve(y_test,svc.decision_function(X_test))

precision_recall_curve函数返回一个列表，包含按顺序排序的所有可能阈值（在决策函数中出现的所有值）对应的准确率和召回率，这样我们就可以绘制一条曲线：

from sklearn.datasets import load_digits,make_blobs
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.metrics import precision_recall_curve
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = FalseX,y=make_blobs(n_samples=(4000,500),cluster_std=[7.0,2],random_state=22)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
svc=SVC(gamma=0.05).fit(X_train,y_train)precision,recall,thresholds=precision_recall_curve(y_test,svc.decision_function(X_test))
close_zero=np.argmin(np.abs(thresholds))
plt.plot(precision[close_zero],recall[close_zero],'o',markersize=10,label='阈值 0',fillstyle='none',mew=2)
plt.plot(precision,recall,label='精确率-召回率曲线')
plt.xlabel('准确率')
plt.ylabel('召回率')
plt.show()

上图中曲线上的每一个点都对应decision_function的一个可能阈值。例如，我们可以看到，在准确率约为0.75的时候，召回率为0.4.黑色圆圈表示的是阈值为0的点，0是decision_function的默认阈值，这个点是在调用predict方法时所选择的折中点。

曲线越靠近右上角，则分类器越好。右上角的点表示对于同一个阈值，准确率和召回率都很高。曲线从左上角开始，这里对应于非常低的阈值，将所有样本都化为正类。提高阈值可以让曲线向准确率更高的方向移动，但同时召回率降低。继续增大阈值，大多数被划为正类的点都是真正例，此时准确率很高，但召回率更低，随着准确率的升高，模型越能够保持较好的召回率，则模型越好。

进一步观察曲线，可以发现，利用这个模型可以得到约0.5的准确率，同时保持很高的召回率。如果我们想要更高的准确率，那么就必须牺牲很多召回率。换句话说，曲线左侧相对平坦，说明在准确率提高的同时召回率没有下降很多。当准确率大于0.5之后准确率每增加一点就会导致召回率下降很多。

不同的分类器可能在曲线上不同的位置（即在不同的工作点）表现很好，我们来比较一下再同一数据集上训练的SVM与随机森林。RandomForestClassifier没有decision_function，只有predict_proba。precision_recall_curve函数的第二个参数应该是正类的确定性度量，所以我们传入样本属于类别1的概率。二分类问题的predict_proba的默认阈值为0.5，所以我们在曲线上标出这个点：

import mglearn.plots
from sklearn.datasets import load_digits,make_blobs
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.metrics import precision_recall_curve
import numpy as np
from sklearn.ensemble import RandomForestClassifier
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = FalseX,y=make_blobs(n_samples=(4000,500),cluster_std=[7.0,2],random_state=22)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
svc=SVC(gamma=0.05).fit(X_train,y_train)
rf=RandomForestClassifier(n_estimators=100,random_state=0,max_features=2)
rf.fit(X_train,y_train)precision,recall,thresholds=precision_recall_curve(y_test,svc.decision_function(X_test))
close_zero=np.argmin(np.abs(thresholds))
precision_rf,recall_rf,thresholds_rf=precision_recall_curve(y_test,rf.predict_proba(X_test)[:,1])
plt.plot(precision,recall,label='svc')
plt.plot(precision[close_zero],recall[close_zero],'o',markersize=10,label='阈值 0(SVC)',fillstyle='none',mew=2)
plt.plot(precision_rf,recall_rf,label='rf')
close_default_rf=np.argmin(np.abs(thresholds_rf-0.5))
plt.plot(precision_rf[close_default_rf],recall_rf[close_default_rf],'^',c='k',markersize=10,label='阈值 0.5 rf',fillstyle='none',mew=2)
plt.xlabel('准确率')
plt.ylabel('召回率')
plt.legend(loc='best')
plt.show()

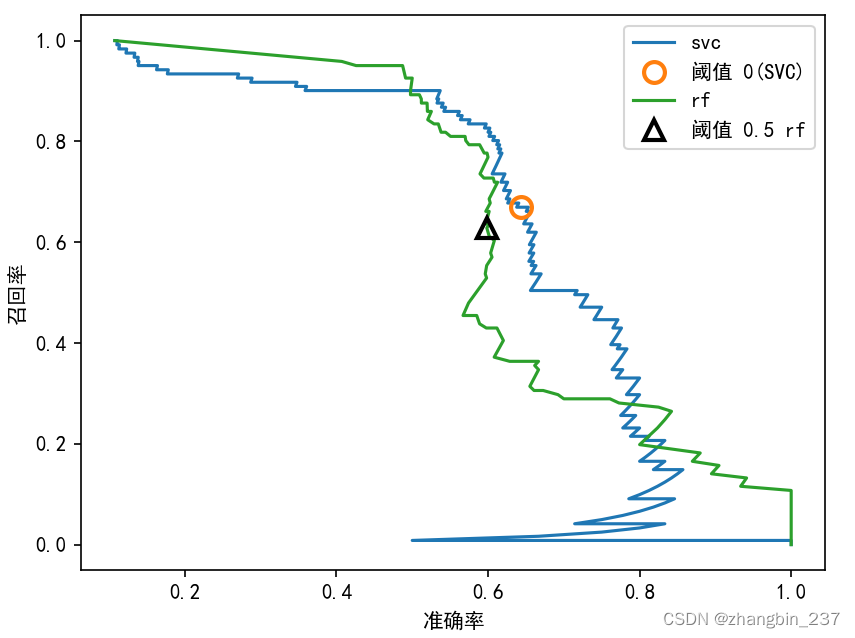
从这张对比图可以看出，随机森林在极值处（要求很高的召回率或很高的准确率）的表现更好。在中间位置（准确率约为0.7）SVM的表现更好。如果我们只查看 $f_{1}$ -分数来比较二者的总体性能，那么可能会遗漏这些细节。 $f_{1}$ -分数只反映了准确率-召回率曲线上的一个点，即默认阈值对应的那个点。

print('随机森林f1-分数:{:.3f}'.format(f1_score(y_test,rf.predict(X_test))))
print('SVC f1-分数:{:.3f}'.format(f1_score(y_test,svc.predict(X_test))))

对比这两条准确率-召回率曲线，可以为我们提供大量详细的洞见，但这是一个相当麻烦的过程。对于自动化模型对比，我们可能希望总结曲线中包含的信息，而不限于某个特定的阈值或工作点。总结准确率-召回率曲线的一种方法是计算该曲线下的积分或面积，也叫做平均准确率。你可以使用average_precision_score函数来计算平均准确率。因为我们要计算准确率-召回率曲线并考虑多个阈值，所以需要向average_precision_score传入decision_function或predict_proba的结果，而不是predict的结果：

ap_rf=average_precision_score(y_test,rf.predict_proba(X_test)[:,1])
ap_svc=average_precision_score(y_test,svc.decision_function(X_test))
print('平均准确率（随机森林）：{:.3f}'.format(ap_rf))
print('平均准确率（svc）：{:.3f}'.format(ap_svc))

在对所有可能的阈值进行平均时，我们看到随机森林和SVC的表现差不多好。随机森林稍微领先。这与前面从f1_score中得到的结果大卫不同。因为平均准确率是从0到1的曲线下的面积，所以平均准确率总是返回一个在0（最差）到1（最好）之间的值。随机分配decision_function的分类器的平均准确率是数据集中正例样本所占的比例。

6、受试者工作特征（ROC）与AUC

还有一种常用的工具可以分析不同阈值的分类器行为：受试者工作特征曲线，简称为ROC曲线。，与准确率-召回率曲线类似，ROC曲线考虑了给定分类器的所有可能的阈值，但它显示的是假正例率（FPR）和真正例率（TPR），而不是报告准确率和召回率（真正例率只是召回率的另一个名称，而假正例率则是假正例占所有反类样本的比例）。

FPR=FP/(FP+TN)

可以用roc_curve函数来计算ROC曲线：

fpr,tpr,thresholds=roc_curve(y_test,svc.decision_function(X_test))plt.plot(fpr,tpr,label='ROC曲线')
plt.xlabel('FPR')
plt.ylabel('TPR(recall)')
close_zero=np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero],tpr[close_zero],'o',markersize=10,label='阈值0',fillstyle='none',c='k',mew=2)
plt.legend(loc=4)
plt.show()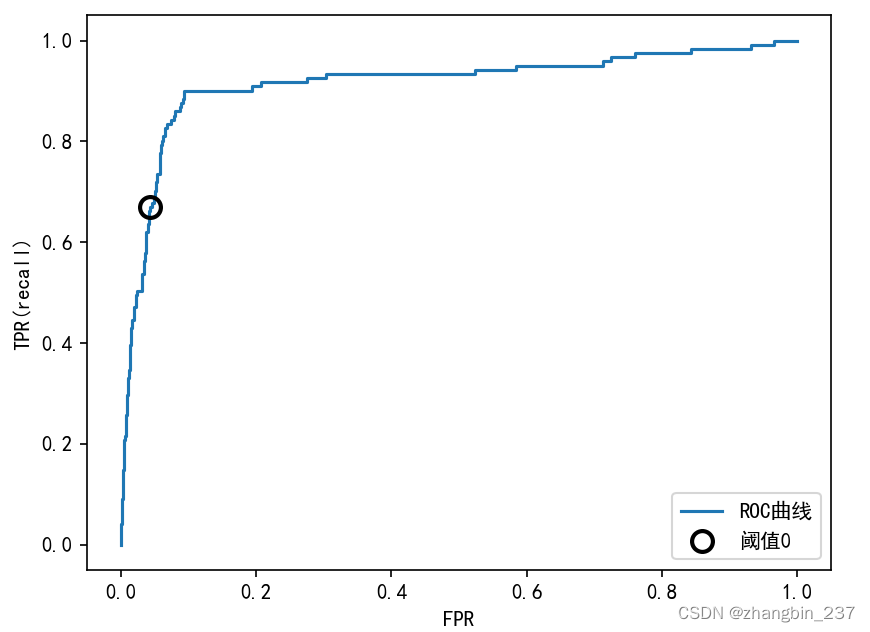

对于ROC曲线，理想的曲线要靠近左上角：我们希望分类器的召回率很高，同时保证假正例率很低。从曲线中可以看出，与默认阈值0相比，我们可以得到明显更高的召回率（约为0.9），而FPR仅稍有增加。最接近左上角的点可能是比默认选择更好的工作点。同样要注意，不应该在测试集上选择阈值，而是应该在单独的验证集上选择。

下图给出了随机森林和SVM的ROC曲线对比：

fpr,tpr,thresholds=roc_curve(y_test,svc.decision_function(X_test))
close_zero=np.argmin(np.abs(thresholds))
fpr_rf,tpr_rf,thresholds_rf=roc_curve(y_test,rf.predict_proba(X_test)[:,1])plt.plot(fpr,tpr,label='ROC曲线（SVC）')
plt.plot(fpr_rf,tpr_rf,label='ROC曲线（随机森林）')
plt.xlabel('FPR')
plt.ylabel('TPR(recall)')
plt.plot(fpr[close_zero],tpr[close_zero],'o',markersize=10,label='SVC 阈值0',fillstyle='none',c='k',mew=2)
close_default_rf=np.argmin(np.abs(thresholds_rf-0.5))
plt.plot(fpr_rf[close_default_rf],tpr_rf[close_default_rf],'^',markersize=10,label='随机森林 阈值0.5',fillstyle='none',c='k',mew=2)
plt.legend(loc=4)
plt.show()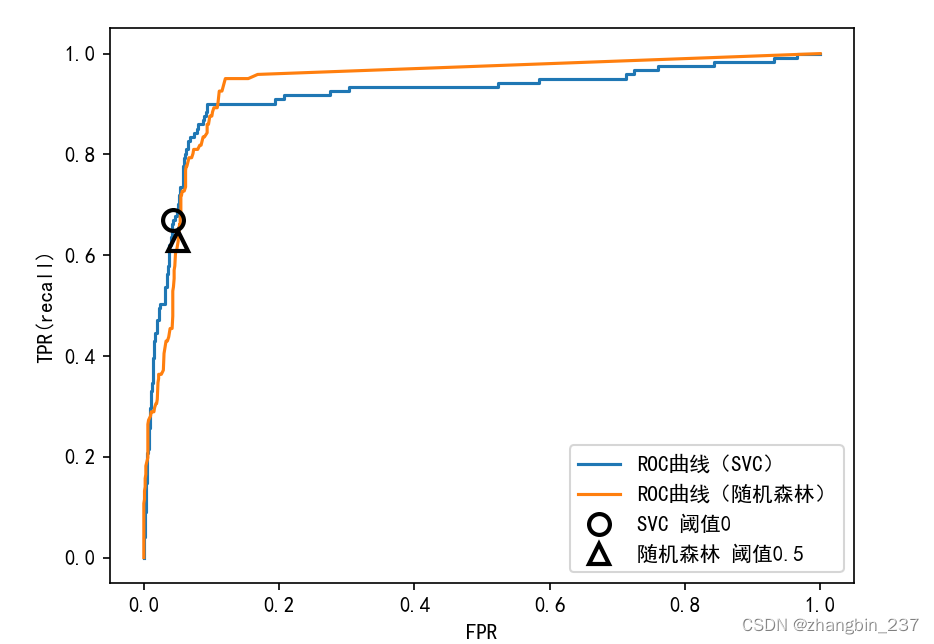

与准确率-召回率曲线一样，我们通常希望使用一个数字来总结ROC曲线，即曲线下的面积（通常被称为AUC，这里的曲线指的就是ROC曲线）。我们可以利用roc_auc_score函数来计算ROC曲线下的面积：

rf_auc=roc_auc_score(y_test,rf.predict_proba(X_test)[:,1])
svc_auc=roc_auc_score(y_test,svc.decision_function(X_test))
print('AUC(随机森林):{:.3f}'.format(rf_auc))
print('AUC(SVC):{:.3f}'.format(svc_auc))

利用AUC分数来比较随机森林和SVM，我们发现随机森林的表现比SVM要略好一些。由于平均准确率是从0到1的曲线下的面积，所以平均准确率总是返回一个0到1之间的值。随机预测得到的AUC总是等于0.5，无论数据集中的类别多么不平衡。对于不平衡的分类问题来说，AUC是一个比精度好得多的指标。AUC可以被解释为评估整理样本的排名。它等价于从正类样本中随机挑选一个点，由分类器废除的分数比从反类样本中随机挑选一个点的分数更高的概率。因此，AUC最高为1，这说明所有正类点的分数高于所有反类点。对于不平衡类别的分类问题，使用AUC进行模型选择通常比使用精度更有意义。

我们使用SVM对之前（9&非9）数据集进行分类，分别使用三种不同的内核宽度（gamma）设置：

from sklearn.datasets import load_digits,make_blobs
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVC
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.metrics import roc_curve,roc_auc_scoredigits=load_digits()
y=digits.target==9
X_train,X_test,y_train,y_test=train_test_split(digits.data,y,random_state=0)
plt.figure()for gamma in [1,0.1,0.01]:svc=SVC(gamma=gamma).fit(X_train,y_train)accuracy=svc.score(X_test,y_test)auc = roc_auc_score(y_test, svc.decision_function(X_test))fpr, tpr, _ = roc_curve(y_test, svc.decision_function(X_test))print('gamma={:.2f} accuracy={:.2f} AUC={:.2f}'.format(gamma,accuracy,auc))plt.plot(fpr,tpr,label='gamma={:.3f}'.format(gamma))plt.xlabel('FPR')
plt.ylabel('TPR')
plt.xlim(-0.01,1)
plt.ylim(0,1.02)
plt.legend(loc='best')
plt.show()

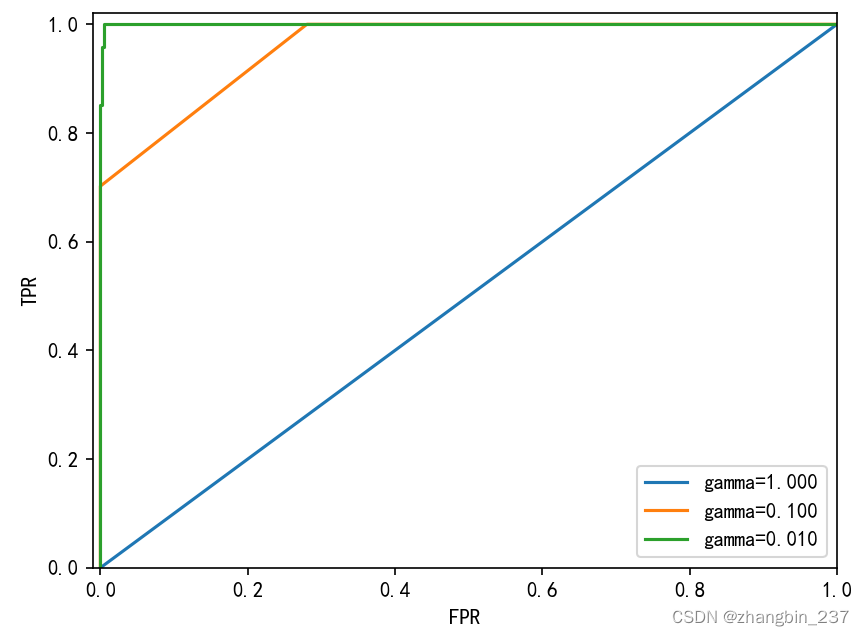
对于3中不同的gamma设置，其精度是相同的，都等于0.9，这可能与随机森林的性能相同，也可能不同。但是观察AUC以及对应的曲线，我们可以看到三个模型之间有明显区别。对于gamma=1.0，AUC实际上处于随机水平，即decision_function的输出与随机结果一样好。对于gamma=0.1，性能大幅提升至AUC等于0.96。最后，对于gamma=0.01，我们得到了等于1 的完美AUC，这意味着根据决策函数，所有正类点的排名要高于所有反类点。换句话说，利用正确的阈值，这个模型可以对所有数据进行完美分类。