矩阵计算在CUDA中的应用是并行计算领域的典型场景 ;
矩阵算法题通常涉及线性代数的基础知识,以及对数据结构和算法的深入理解。解决这类问题时,掌握一些核心思想和技巧会非常有帮助。以下是一些常见的矩阵算法题解题思想:
动态规划:矩阵链乘法问题是一个典型的例子,它要求找出最优的括号化方式来最小化乘法次数。动态规划通过构建一个表来存储子问题的解,从而避免重复计算,达到高效求解的目的。
分治策略:在处理大规模矩阵运算时,如大矩阵乘法,可以考虑分治法,即将大矩阵分割成小矩阵,先计算小矩阵的乘积,再合并结果。Strassen算法就是一个经典的分治算法,它将矩阵分为四个子矩阵,通过7次较小矩阵的乘法来计算原矩阵的乘积,而非传统的8次。
空间换时间:预计算和缓存技术可以用来加速某些类型的矩阵操作,例如计算矩阵的幂。通过预先计算并存储中间结果,后续计算可以复用这些结果,减少重复计算,尽管这可能会增加内存消耗。
位运算:在处理特殊类型的矩阵(如稀疏矩阵或二进制矩阵)时,位运算可以极大地提高效率。例如,利用位运算进行集合运算(交、并、差)可以比传统循环更快。
迭代与递归:在解决某些矩阵问题时,如计算矩阵的特征值、行列式或幂,迭代法和递归法可以提供不同的解决方案。迭代通常用于连续逼近问题,而递归则常用于分解问题为更小规模的相似问题。
利用矩阵特性:理解和利用矩阵的性质(如对称性、正定性、稀疏性)可以简化算法设计。例如,对称矩阵的乘法可以优化存储和计算,稀疏矩阵则可以通过压缩存储格式来节省空间和计算资源。
线性代数变换:诸如LU分解、QR分解、奇异值分解(SVD)等线性代数中的矩阵分解技术,可以将复杂问题转化为更易于处理的形式。这些方法在解决逆矩阵、最小二乘问题、特征值问题等方面非常有效。
73. 矩阵置零
给定一个
m x n的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
思想:
既然要对矩阵中为零的元素的同行、同列都要置为0;
简单的:记住元素0 的行以及列;
在Python中,列表(list)的拷贝可以通过两种主要方式实现:浅拷贝(shallow copy)和深拷贝(deep copy)。这两种拷贝方式的主要区别在于它们处理列表中嵌套对象(如子列表或其他可变对象)的方式。
浅拷贝:里面有复杂结构的不会被拷贝;
浅拷贝创建了一个新列表,但这个新列表中的元素仍然是原列表中元素的引用。这意味着,如果原列表中含有其他可变对象(如子列表),新列表中的对应元素会指向相同的子列表对象。因此,修改新列表中的子列表会影响到原列表中的相应子列表。
浅拷贝可以通过以下方法实现:
- 使用列表的
copy()方法:new_list = original_list.copy()- 使用切片操作:
new_list = original_list[:]深拷贝:里面有复杂结构的也会被拷贝;
深拷贝则不仅创建列表的新副本,还会递归地拷贝列表中所有层级的元素,为所有嵌套的对象创建新的独立副本。因此,修改深拷贝得到的新列表中的任何元素,都不会影响到原列表或其嵌套对象。
深拷贝可以通过以下方法实现:
- 使用
copy模块的deepcopy()函数:import copy; new_list = copy.deepcopy(original_list)import copy class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""rows = []cols = []for i in range(len(matrix)):for j in range(len(matrix[0])):if matrix[i][j] == 0:rows.append(i) cols.append(j)for row,col in zip(rows,cols):matrix[row] = [0] * len(matrix[0])for z in range(len(matrix)):matrix[z][col] = 0
54. 螺旋矩阵
这个题目我遇到很多次了,真的是让我又爱又恨呢,孽缘啊!值的多看看几遍的题目;
给你一个
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
思想:
到底怎么走的呢:
根据题目示例 matrix = [[1,2,3],[4,5,6],[7,8,9]] 的对应输出 [1,2,3,6,9,8,7,4,5] 可以发现,顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。
因此,考虑设定矩阵的 “左、上、右、下” 四个边界,模拟以上矩阵遍历顺序。
算法流程:
1 空值处理: 当 matrix 为空时,直接返回空列表 [] 即可。
2 初始化: 矩阵 左、右、上、下 四个边界 l , r , t , b ,用于打印的结果列表 res 。
3 循环打印: “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印。
- 根据边界打印,即将元素按顺序添加至列表 res 尾部。
- 边界向内收缩 1 (代表已被打印)。
- 判断边界是否相遇(是否打印完毕),若打印完毕则跳出。
4 返回值: 返回 res 即可。
class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:if not matrix:return []l,r,t,b,res = 0,len(matrix[0])-1,0,len(matrix)-1,[]while True:for i in range(l,r+1): res.append(matrix[t][i])t+=1if t>b:breakfor i in range(t,b+1): res.append(matrix[i][r])r-=1if l>r:breakfor i in range(r,l-1,-1): res.append(matrix[b][i])b-=1if t>b:breakfor i in range(b,t-1,-1): res.append(matrix[i][l])l+=1if l>r:breakreturn res
48. 旋转图像
MD! 这个题目,让我想到了在做计算机视觉时图像赠强!
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
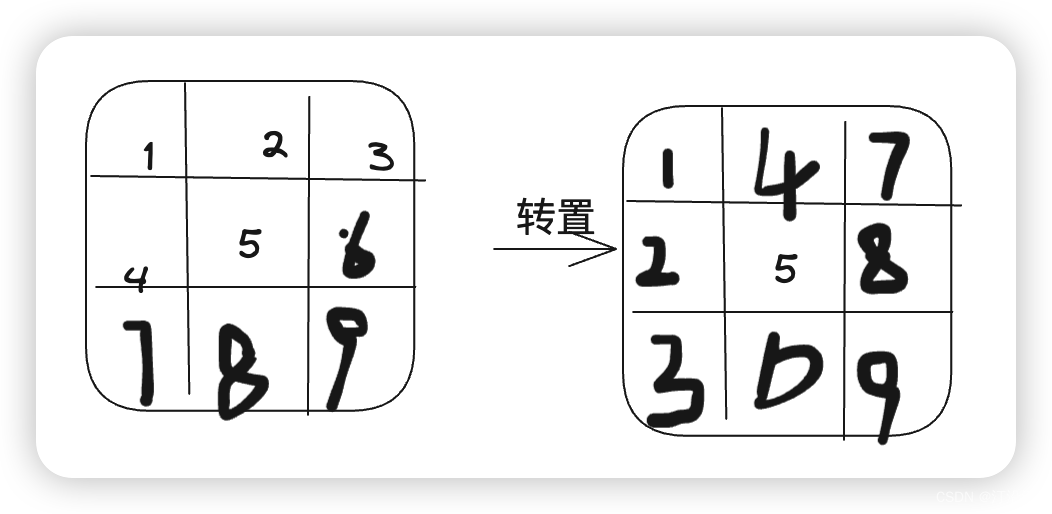
先转置,然后把每一列翻转;
这个想法,我最想到的就是把矩阵转置了;然后看了一下,知道了答案是什么!
zip(*matrix) =矩阵的列转置;在Python中,
zip(*matrix)是一种常用的操作,尤其在处理多维数组(如矩阵)时。这里的matrix假定是一个二维列表(即列表的列表),用于表示一个矩阵。星号(*)在函数调用中的作用是 unpacking(解包),它将矩阵的每一行作为单独的参数传递给zip函数。
zip函数的基本功能是将多个可迭代对象(在这个上下文中是矩阵的行)对应位置的元素配对,形成一个元组的迭代器。当应用于二维列表(矩阵)时,zip(*matrix)的效果是将矩阵的列转置。也就是说,它会把矩阵的每一列元素收集起来,形成新的元组,这些元组组成的迭代器实质上代表了原矩阵的转置。
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""for i in range(len(matrix)):for j in range(i, len(matrix[0])):matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]for i in range(len(matrix)):matrix[i] = matrix[i][::-1]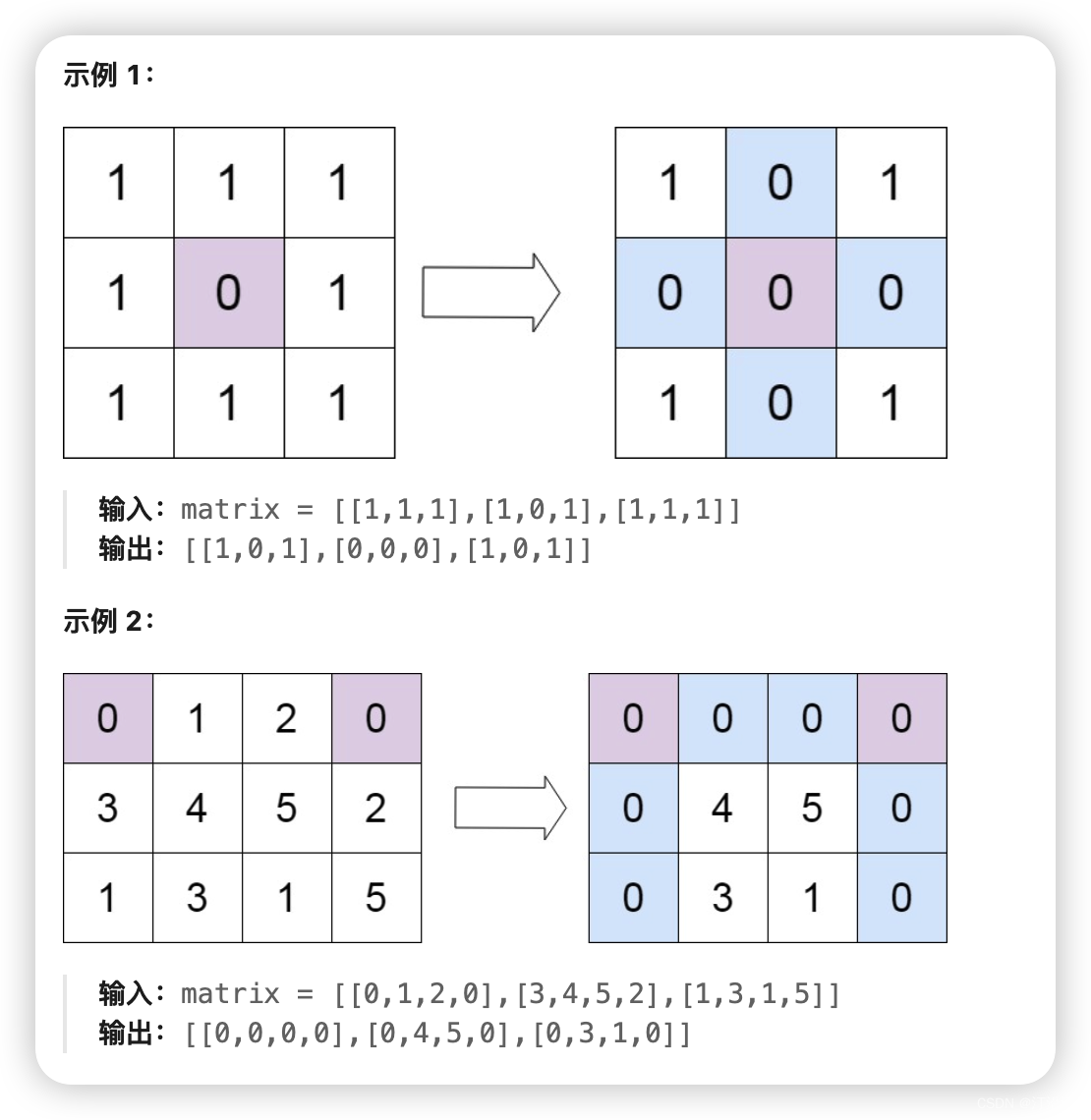






)


![[论文精读]Variational Graph Auto-Encoders](http://pic.xiahunao.cn/[论文精读]Variational Graph Auto-Encoders)




)



)

概述)
)