2024.6.30周报

摘要

ABSTRACT

一、文献阅读

一、题目

二、摘要

三、模型架构

四、文章解读

一、Introduction

二、创新点

三、RBM

四、贪心算法

五、实验

六、结论

二、代码复现

总结

摘要

本周我阅读了一篇题目为Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs的文献，PINN在多查询和实时仿真设置下仍然很耗时，它的参数化往往过于过度，这篇文章提出的生成与训练PINN来缓解参数PDE设置的这两个挑战，然后对文章中给的代码进行了复现，进一步理解了模型的逻辑。

ABSTRACT

This week, I read a paper titled "Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs." PINNs remain time-consuming in multi-query and real-time simulation settings, and their parameterization is often excessive. The article proposes generating and training PINNs to alleviate these two challenges associated with parametric PDE settings. I then replicated the code provided in the paper to further understand the logic of the model.

一、文献阅读

一、题目

题目：GPT-PINN: Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs

期刊：Finite elements in analysis & design

链接：https://arxiv.org/pdf/2303.14878

二、摘要

PINN在多查询和实时仿真设置下仍然很耗时，它的参数化往往过于过度。本文提出了生成与训练PINN来缓解参数PDE设置的这两个挑战，GPT-PINN代表了一种全新的参数系统元学习范式，它的外/元网络是超精简的，只有一个隐藏层，神经元数量显著减少，它在每个隐藏神经元上的激活函数是在明智选择的系统配置下预训练的PINN，元网络自适应地”学习“系统的参数依赖性，并一次一个神经元地”增长“这个隐藏层。最后通过包含在这组自适应选择的参数值上训练的极少数网络，元网络能够准确有效地为整个参数域的参数系统生成替代解决方案。

PINN remains time-consuming under multi-query and real-time simulation settings, and its parameterization is often overly excessive. This paper proposes the generative and trained PINN to alleviate these two challenges in the parametric PDE settings. GPT-PINN represents a brand-new meta-learning paradigm for parametric systems. Its outer/meta-network is hyper-reduced, featuring only one hidden layer with a significantly reduced number of neurons. The activation function at each hidden neuron is a PINN that has been pre-trained under judiciously selected system configurations. The meta-network adaptively "learns" the system's parametric dependencies and "grows" this hidden layer one neuron at a time. Ultimately, by encompassing a very small number of networks trained on this set of adaptively selected parameter values, the meta-network is capable of generating surrogate solutions for the parametric system across the entire parameter domain accurately and efficiently.

三、模型架构

图的组成部分

1、超降阶神经网络（Hyper-reduced Neural Network）:

(1)网络的节点使用预训练的物理信息神经网络（PINNs）作为激活函数。

(2)每个预训练的PINN对应于特定的参数值 $\mu ^{1},\mu ^{2}...,\mu ^{n}$ ，这些参数值在训练过程中被选择以代表不同的物理或计算情境。

(3)神经网络的输入包括空间位置x和时间t，输出 $u_{N}(x,t;\mu )$ 为参数 $\mu$ 下的PDE的解。

2、生成式在线组件（Generative Online Component）:

(1)这部分用于在给定新的参数提示 $\mu$ 时，动态生成PDE解的过程。

(2)包括处理偏微分方程、边界条件和初始条件的各种运算和微分。

(3)利用自动微分技术预计算值和导数，以便快速响应。

目标是通过训练权重 $c_{1}(\mu ),c_{2}(\mu )...c_{n}(\mu )$ 最小化在新参数 $\mu$ 下的损失。

工作原理

输入层：接收空间和时间的输入值x和t，这些是PDE求解中的常见变量。

隐藏层：由预训练的PINNs构成，每个PINN都是在特定参数设置下预训练的，能够快速响应相关参数的变化。

输出层：生成PDE在新的参数设置 $\mu$ 下的解 $u_{N}(x,t;\mu )$ 。

四、文章解读

一、Introduction

文章阐述了在许多应用中，准确且高效地理解系统在多参数变化下的行为是一个普遍需求，如不确定性量化、逆问题、数据同化或最优控制/设计。文中提到，研究系统行为及其对参数的依赖需要进行大量的偏微分方程（PDE）模拟，这在使用传统数值方法时，尤其是在需要大量重复模拟的情况下，将是计算上的挑战。文章提出了基于深度学习的两种主要技术来应对这一挑战：传统的降阶建模和新兴的深度神经网络。降阶基方法（RBM）作为一种基于投影的模型降阶方法，能够生成参数化问题的计算模拟器，并具有与全问题相比的认证误差。而物理信息神经网络（PINN）则采用深度神经网络来代表PDE的近似解决方案，相较于传统数值解法，PINN能够定义整个连续的空间时间域上的函数，并依赖于自动微分技术。尽管PINN展示了其优势，但在多查询和实时模拟环境中，PINN的训练仍然耗时且其参数化通常过度。因此，文章引入了生成预训练PINN（GPT-PINN），这是一种全新的参数系统元学习范式。通过在精简的外部/元网络中预训练的PINN作为激活函数，GPT-PINN能够适应性地"学习"系统的参数依赖性，并在整个参数域内准确且高效地生成替代解决方案。

二、创新点

1、将整个（预训练）的网络用作单个神经元的激活函数。

2、采用元网络的训练损失作为误差指标，收到传统数值求解器（FEM）基于残差的误差估计的启发。

三、RBM

RBM（Reduced Basis Method）是一种线性降阶方法，被广泛用于精确且高效地模拟参数化偏微分方程（PDEs）。其核心特征是利用离线-在线分解过程中嵌入的贪心算法。

1、离线阶段

在离线（即训练）阶段，RBM专注于通过数学严谨的贪心算法来探索由参数引起的解流形，从而选择一系列代表性的参数值。这一阶段的目的是为在线计算构建一个终端代理空间，并从中寻求每个未见参数值的简化解。

2、在线阶段

在在线阶段，针对每个新的参数值，都会在终端代理空间中寻求一个简化解。与其他降阶技术（如基于适当正交分解（POD）的方法）不同，RBM在离线阶段进行的全序查询次数最少，即等于代理空间的维度。

在给定 μ 的情况下，这种简化阶模型（ROM）的表述被称为 ROM( $\mu ,X_{N}$ )，其解决成本远低于 FOM( $\mu ,X_{h}$ )，并可以在在线阶段进行。

四、贪心算法

GPT-PINN离线训练阶段的流程图，详细展示了如何训练生成预训练物理信息神经网络（GPT-PINN），用于参数化偏微分方程（PDE）。以下是流程图中各个步骤的详细解释:

输入：随机或指定的初始参数 $\mu ^{1}$ ，一个训练集 $\Xi _{train}$ ，以及一个完整的物理信息神经网络（Full PINN）。

训练步骤：

1、在 $\mu ^{1}$ 上训练全PINN：在置顶的参数 $\mu ^{1}$ 上训练一个完整的PINN，获取 $\Psi _{\Theta _{1}}^{NN}$ ，这是对应于 $\mu ^{1}$ 的解的神经网络表达。

2、初始化的迭代训练：

(1)设置 n=2，开始迭代过程。

(2)对于训练集中的每个 $\mu$ ，训练一个简化的GPT-PINN网络 NN(2,n−1,1) 并记录错误指标 $\Delta _{n-1}(\mu )$ 。

(3)选择下一个参数 $\mu ^{n}$ ，它使得 $\Delta _{n-1}(\mu )$ 最大，即选择误差最大的参数进行进一步训练。

(4)在新选定的 $\mu ^{n}$ 上训练全PINN，得到新的神经网络表达 $\Psi _{\Theta _{n}}^{NN}$ 。

(5)更新GPT-PINN，向隐藏层添加一个新神经元，构建NN(2,n,1)。

(6)n←n+1，继续迭代直至满足停止条件。

输出：训练完成的GPT-PINN NN(2,N,1)，其中 NNN 是最终的神经元索引。

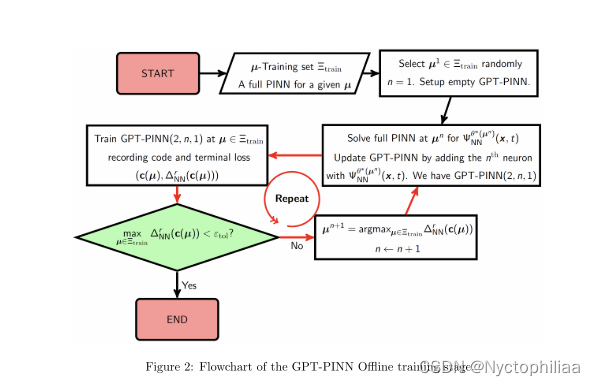
如上图所示：

(1)流程图从“开始”标志开始，首先选择一个参数 $\mu ^{1}$ 并设置一个空的GPT-PINN。

(2)经过一系列的训练和选择步骤，不断迭代增加网络的复杂性。

(3)每次迭代都涉及在当前网络上训练，并基于误差指标选择新的参数进行下一轮训练。

(4)当误差指标 $\bigtriangleup _{n}(\mu (c(\mu )))$ 小于某个阈值 $\varepsilon$ 或达到其他停止条件时，流程结束。

五、实验

本文将GPT-PINN应用于Klein-Gordon方程、Burgers’方程和Allen-Cahn方程三类方程的数值结果。

1、Klein-Gordon Equation

首先测试Klein-Gordon方程参数化为 $(\alpha ,\beta ,\gamma )$ $\epsilon$ [-2,-1] $\times$ [0,1] $\times$ [0,1]

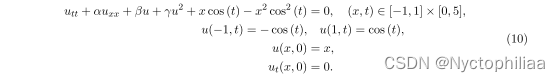
full PINN是一个具有激活函数cos(z)的[2,40,40,1]的全连接网络，它使用均匀分布的配点来训练，其中| $C_{o}$ |=10000，| $C_{\partial }$ |=512，| $C_{i}$ |=512，ADAM优化器的学习率为0.0005，最大epoch数为75000，参数训练集 $\Xi _{train}$ 是一个大小10 $\times$ 10 $\times$ 10的张量网格，共有1000个参数值，贪心算法产生的gpt - pin的大小为[2,1,1]到[2,15,1]，最多可生成15个神经元。

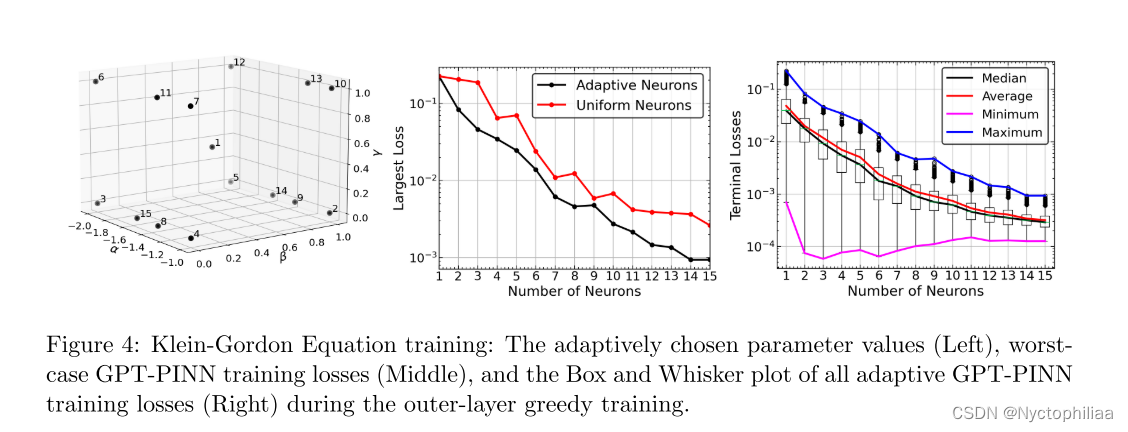
左图是一个三维散点图，显示了参数 $(\alpha ,\beta ,\gamma )$ 的选择分布。每个点代表一个参数组合，点上的数字表示按贪心算法选择参数的顺序。这种分布可帮助我们了解在参数空间中，哪些区域被认为是对模型训练影响最大的，因此优先被选择进行训练。

中间的图展示了两种不同类型的神经元训练策略——自适应神经元和均匀神经元——随着神经元数量增加的最大训练损失。这表明自适应选择可以更有效地减少模型的误差，尤其是在初始阶段。

右图是Box and Whisker图，显示了训练过程中所有自适应GPT-PINN训练损失的统计数据。损失的快速减少表明了模型在迭代过程中对Klein-Gordon方程解的逼近逐渐提高，尤其是中位数和平均数线表明了主要的趋势。

2、Burgers’ Equation

接下来，我们用一个参数，粘度ν∈[0.005,1]，在Burgers方程上测试GPT-PINN。

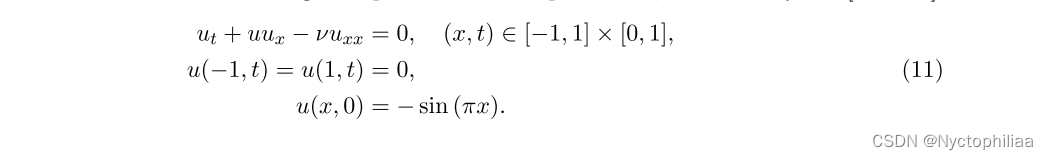
完整PINN是一个具有激活函数tanh(z)的[2,20,20,20,20,20,20,1]全连接网络，使用均匀分布的配点训练，| $C_{o}$ | = 10,000， | $C_{\partial }$ | = 100，| $C_{i}$ | = 100。ADAM优化器的学习率为0.005。最大次数为60000次，在损失值上实现 $2\times 10^{-5}$ 的停止标准。参数训练集是ν域中大小为129的均匀网格。贪心算法产生的gpt - pinn的大小为[2,1,1]至[2,9,1]，最多可生成9个神经元。gptpinn在与完整PINN相同的搭配点集上进行训练，但学习率为0.02和2000 epoch。

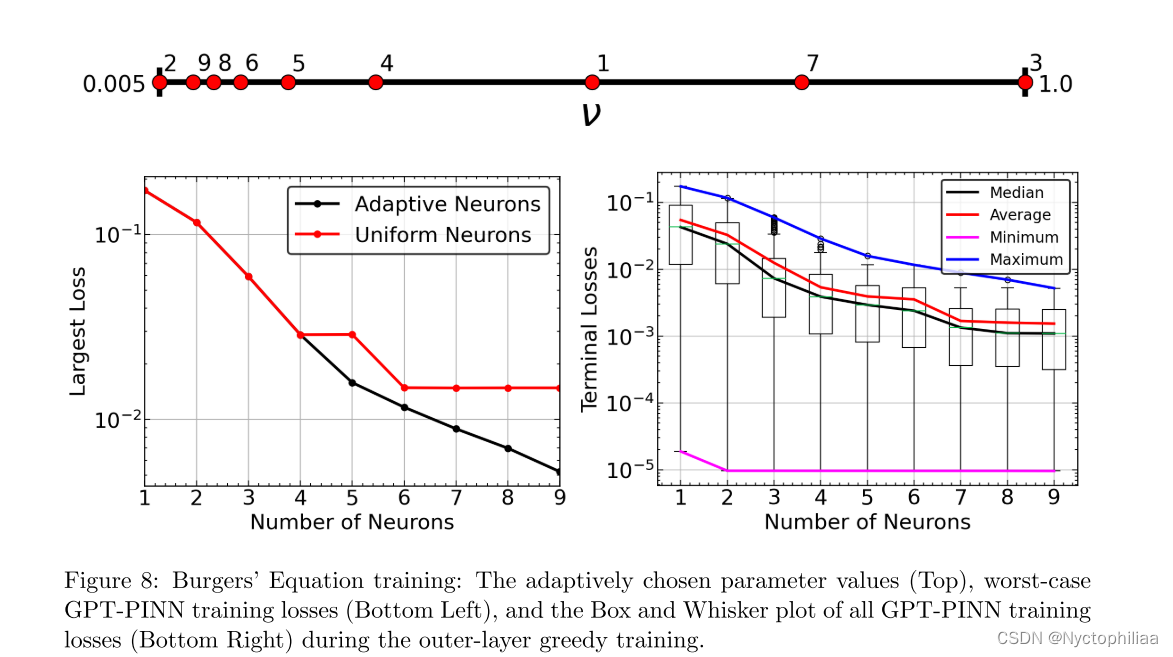
与Klein-Gordon方程的结果类似，自适应“学习神经元”的表现再次比非自适应“统一神经元”好3到4倍。

这张图展示了用于Burgers'方程的物理信息神经网络（PINN）和生成预训练物理信息神经网络（GPT-PINN）的训练损失以及解的点误差分布。整体来看，这张图有效地展示了全PINN和GPT-PINN在处理Burgers'方程时的性能差异。特别是GPT-PINN在训练效率和损失收敛速度上显示出了显著的优势。通过这些观察，可以评估使用GPT-PINN对于快速求解参数化PDEs的潜在益处，尤其是在需要处理多参数或实时仿真场景的应用中。

六、结论

本文提出的生成式预训练PINN (GPT-PINN)缓解了参数化pde设置中PINN面临的两个挑战，即训练成本和过度参数化。GPT-PINN是一个具有预训练的激活函数的超简化网络，代表了参数系统的一种全新的元学习范式。本文提出了两个主要的新颖之处，即网络结构的设计，包括其特殊的激活函数和采用元网络的训练损失作为误差指标，并通过对三个微分族参数方程的测试，已经证明，包含非常少量的精心选择的网络可以在整个参数域准确有效地生成代理PINN。

二、代码复现

# Import and GPU Support
import matplotlib.pyplot as plt
import numpy as np
import torch
import os
import tensorflow as tfphysical_devices = tf.config.list_physical_devices('GPU') 
tf.config.experimental.set_memory_growth(physical_devices[0], True)import time
import scipy.io
from tensorflow import keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras import layers, activations
from eager_lbfgs import lbfgs, Struct
from pyDOE import lhs
np.random.seed(1234) # lhs# GPT-PINN
from AC_Plotting import AC_plot, loss_plot from AC_GPT_activation import P
from AC_GPT_precomp import autograd_calculations, Pt_lPxx_eP
from AC_GPT_PINN import GPT
from AC_GPT_train import gpt_train# SA-PINN is implemented explicitly in the codetorch.set_default_dtype(torch.float)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Current Device (PyTorch): {device}")
if torch.cuda.is_available():print(f"Current Device Name (PyTorch): {torch.cuda.get_device_name()}")# Domain and Data
data_path = r".\data"
xt_test = torch.from_numpy(np.loadtxt(fr"{data_path}\xt_test.txt",dtype=np.float32)).to(device)# Initial Condition
IC_x = torch.from_numpy(np.loadtxt(fr"{data_path}\initial\x0.txt",dtype=np.float32))
IC_t = torch.zeros(IC_x.shape[0])[:,None]
val, idx = torch.sort(IC_x)
IC_u = torch.from_numpy(np.loadtxt(fr"{data_path}\initial\u0.txt",dtype=np.float32))
IC_u = IC_u[idx][:,None].to(device)
IC_xt = torch.hstack((IC_x[idx][:,None],IC_t)).to(device)# Boundary Condition
BC_x_ub = torch.from_numpy(np.loadtxt(fr"{data_path}\boundary\x_ub.txt",dtype=np.float32))[:,None]
BC_t_ub = torch.from_numpy(np.loadtxt(fr"{data_path}\boundary\t_ub.txt",dtype=np.float32))[:,None]
BC_xt_ub = torch.hstack((BC_x_ub,BC_t_ub))BC_x_lb = torch.from_numpy(np.loadtxt(fr"{data_path}\boundary\x_lb.txt",dtype=np.float32))[:,None]
BC_t_lb = torch.from_numpy(np.loadtxt(fr"{data_path}\boundary\t_lb.txt",dtype=np.float32))[:,None]
BC_xt_lb = torch.hstack((BC_x_lb,BC_t_lb))BC_xt = torch.vstack((BC_xt_ub,BC_xt_lb)).to(device) 
BC_u = torch.full((200,1), -1.0).to(device)  # Residual 
x_resid = torch.from_numpy(np.loadtxt(fr"{data_path}\f\xf_train.txt",dtype=np.float32))[:,None]
t_resid = torch.from_numpy(np.loadtxt(fr"{data_path}\f\tf_train.txt",dtype=np.float32))[:,None]xt_resid = torch.hstack((x_resid,t_resid)).to(device) 
f_hat = torch.full((20000,1), 0.0).to(device)   # Training Parameter Set
ac_training = np.loadtxt("ac_param_training.txt")train_final_gpt   = True
number_of_neurons = 9
loss_list         = np.ones(number_of_neurons)
print(f"Expected Final GPT-PINN Depth: {[2,number_of_neurons,1]}\n")###############################################################################
#################################### GPT Setup ####################################
###############################################################################
P_resid_values    = torch.ones((xt_resid.shape[0],  number_of_neurons)).to(device)
P_IC_values       = torch.ones((   IC_xt.shape[0],  number_of_neurons)).to(device)
P_BC_values       = torch.ones((   BC_xt.shape[0],  number_of_neurons)).to(device)P_t_term  = torch.ones((xt_resid.shape[0], number_of_neurons)).to(device)
P_xx_term = torch.ones((xt_resid.shape[0], number_of_neurons)).to(device)ac_neurons    = [1 for i in range(number_of_neurons)]
ac_neurons[0] = [0.00055, 3.0]P_list = np.ones(number_of_neurons, dtype=object)lr_gpt          = 0.0025
epochs_gpt      = 2000
epochs_gpt_test = 5000
test_cases      = 25# Save Data/Plot Options
save_data         = False
plot_pinn_loss    = True
plot_pinn_sol     = True
plot_largest_loss = Truepinn_train_times = np.ones(number_of_neurons)
gpt_train_times  = np.ones(number_of_neurons)total_train_time_1 = time.perf_counter()
###############################################################################
#################################### SA Setup #################################
###############################################################################
# SA-PINN from https://github.com/levimcclenny/SA-PINNslr_adam_sa  = 0.005
lr_lbfgs_sa = 0.8epochs_adam_sa  = 10000
epochs_lbfgs_sa = 10000layers_sa = [2, 128, 128, 128, 128, 1]lb = np.array([-1.0])
ub = np.array([1.0])N0 = 512
N_b = 100
N_f = 20000data = scipy.io.loadmat('AC.mat')
t = data['tt'].flatten()[:,None]
x = data['x'].flatten()[:,None]
Exact = data['uu']
Exact_u = np.real(Exact)#grab training points from domain
idx_x = np.random.choice(x.shape[0], N0, replace=False)
x0 = x[idx_x,:]
u0 = tf.cast(Exact_u[idx_x,0:1], dtype = tf.float32)idx_t = np.random.choice(t.shape[0], N_b, replace=False)
tb = t[idx_t,:]
# Grab collocation points using latin hypercube sampling
X_f = lb + (ub-lb)*lhs(2, N_f)
x_f = tf.convert_to_tensor(X_f[:,0:1], dtype=tf.float32)
t_f = tf.convert_to_tensor(np.abs(X_f[:,1:2]), dtype=tf.float32)# IC/BC data 
X0 = np.concatenate((x0, 0*x0), 1) # (x0, 0)
X_lb = np.concatenate((0*tb + lb[0], tb), 1) # (lb[0], tb)
X_ub = np.concatenate((0*tb + ub[0], tb), 1) # (ub[0], tb)
x0 = tf.cast(X0[:,0:1], dtype = tf.float32)
t0 = tf.cast(X0[:,1:2], dtype = tf.float32)
x_lb = tf.convert_to_tensor(X_lb[:,0:1], dtype=tf.float32)
t_lb = tf.convert_to_tensor(X_lb[:,1:2], dtype=tf.float32)
x_ub = tf.convert_to_tensor(X_ub[:,0:1], dtype=tf.float32)
t_ub = tf.convert_to_tensor(X_ub[:,1:2], dtype=tf.float32)#L-BFGS weight getting and setting from https://github.com/pierremtb/PINNs-TF2.0
def set_weights(model, w, sizes_w, sizes_b):with tf.device('/GPU:0'):for i, layer in enumerate(model.layers[0:]):start_weights = sum(sizes_w[:i]) + sum(sizes_b[:i])end_weights = sum(sizes_w[:i+1]) + sum(sizes_b[:i])weights = w[start_weights:end_weights]w_div = int(sizes_w[i] / sizes_b[i])weights = tf.reshape(weights, [w_div, sizes_b[i]])biases = w[end_weights:end_weights + sizes_b[i]]weights_biases = [weights, biases]layer.set_weights(weights_biases)def get_weights(model):with tf.device('/GPU:0'):w = []for layer in model.layers[0:]:weights_biases = layer.get_weights()weights = weights_biases[0].flatten()biases = weights_biases[1]w.extend(weights)w.extend(biases)w = tf.convert_to_tensor(w)return w#define the neural network model
def neural_net(layer_sizes):with tf.device('/GPU:0'):model = Sequential()model.add(layers.InputLayer(input_shape=(layer_sizes[0],)))for width in layer_sizes[1:-1]:model.add(layers.Dense(width, activation=tf.nn.tanh,kernel_initializer="glorot_normal"))model.add(layers.Dense(layer_sizes[-1], activation=None,kernel_initializer="glorot_normal"))return model#define the loss
def loss(x_f_batch, t_f_batch,x0, t0, u0, x_lb,t_lb, x_ub, t_ub,col_weights, u_weights, lmbda, eps):with tf.device('/GPU:0'):f_u_pred = f_model(x_f_batch, t_f_batch, lmbda, eps)u0_pred = u_model(tf.concat([x0, t0], 1))u_lb_pred, u_x_lb_pred, = u_x_model(u_model, x_lb, t_lb)u_ub_pred, u_x_ub_pred, = u_x_model(u_model, x_ub, t_ub)mse_0_u = tf.reduce_mean(tf.square(u_weights*(u0 - u0_pred)))mse_b_u = tf.reduce_mean(tf.square(tf.math.subtract(u_lb_pred, u_ub_pred))) + \tf.reduce_mean(tf.square(tf.math.subtract(u_x_lb_pred, u_x_ub_pred)))mse_f_u = tf.reduce_mean(tf.square(col_weights * f_u_pred[0]))return  mse_0_u + mse_b_u + mse_f_u , tf.reduce_mean(tf.square((u0 - u0_pred))), mse_b_u, tf.reduce_mean(tf.square(f_u_pred))@tf.function
def f_model(x,t,lmbda,eps):with tf.device('/GPU:0'):u = u_model(tf.concat([x, t],1))u_x = tf.gradients(u, x)u_xx = tf.gradients(u_x, x)u_t = tf.gradients(u,t)c1 = tf.constant(lmbda, dtype = tf.float32)c2 = tf.constant(eps, dtype = tf.float32)f_u = u_t - c1*u_xx + c2*u*u*u - c2*ureturn f_u@tf.function
def u_x_model(u_model, x, t):with tf.device('/GPU:0'):u = u_model(tf.concat([x, t],1))u_x = tf.gradients(u, x)return u, u_x@tf.function
def grad(model, x_f_batch, t_f_batch, x0_batch, t0_batch, u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps):with tf.device('/GPU:0'):with tf.GradientTape(persistent=True) as tape:loss_value, mse_0, mse_b, mse_f = loss(x_f_batch, t_f_batch, x0_batch, t0_batch, u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps)grads = tape.gradient(loss_value, u_model.trainable_variables)grads_col = tape.gradient(loss_value, col_weights)grads_u = tape.gradient(loss_value, u_weights)gradients_u = tape.gradient(mse_0, u_model.trainable_variables)gradients_f = tape.gradient(mse_f, u_model.trainable_variables)return loss_value, mse_0, mse_b, mse_f, grads, grads_col, grads_u, gradients_u, gradients_fdef fit(x_f, t_f, x0, t0, u0, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, tf_iter, newton_iter, lmbda, eps):with tf.device('/GPU:0'):batch_sz = N_f # Can adjust batch size for collocation points, here we set it to N_fn_batches =  N_f // batch_szadam_losses = []#create optimizer s for the network weights, collocation point mask, and initial boundary masktf_optimizer = tf.keras.optimizers.Adam(learning_rate = lr_adam_sa, beta_1=.99)tf_optimizer_weights = tf.keras.optimizers.Adam(learning_rate = lr_adam_sa, beta_1=.99)tf_optimizer_u = tf.keras.optimizers.Adam(learning_rate = lr_adam_sa, beta_1=.99)print("Starting ADAM training")# For mini-batch (if used)for epoch in range(tf_iter):for i in range(n_batches):x0_batch = x0t0_batch = t0u0_batch = u0x_f_batch = x_f[i*batch_sz:(i*batch_sz + batch_sz),]t_f_batch = t_f[i*batch_sz:(i*batch_sz + batch_sz),]loss_value, mse_0, mse_b, mse_f, grads, grads_col, grads_u, g_u, g_f = grad(u_model, x_f_batch, t_f_batch, x0_batch, t0_batch,  u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps)tf_optimizer.apply_gradients(zip(grads, u_model.trainable_variables))tf_optimizer_weights.apply_gradients(zip([-grads_col, -grads_u], [col_weights, u_weights]))if (epoch % 250 == 0) or (epoch == (tf_iter-1)):adam_losses.append(loss_value)if (epoch % 1000 == 0) or (epoch == (tf_iter-1)):print("Epoch: %d | " % (epoch), end='')tf.print(f"mse_0: {mse_0} | mse_b: {mse_b} | mse_f: {mse_f} | Total Loss: {loss_value}\n")print("Starting L-BFGS training")loss_and_flat_grad = get_loss_and_flat_grad(x_f_batch, t_f_batch, x0_batch, t0_batch, u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps)lbfgs_losses = lbfgs(loss_and_flat_grad,get_weights(u_model),Struct(), maxIter=newton_iter, learningRate=lr_lbfgs_sa)[3]return adam_losses, lbfgs_losses#L-BFGS implementation from https://github.com/pierremtb/PINNs-TF2.0
def get_loss_and_flat_grad(x_f_batch, t_f_batch, x0_batch, t0_batch, u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps):def loss_and_flat_grad(w):with tf.device('/GPU:0'):with tf.GradientTape() as tape:set_weights(u_model, w, sizes_w, sizes_b)loss_value, _, _, _ = loss(x_f_batch, t_f_batch, x0_batch, t0_batch, u0_batch, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, lmbda, eps)grad = tape.gradient(loss_value, u_model.trainable_variables)grad_flat = []for g in grad:grad_flat.append(tf.reshape(g, [-1]))grad_flat = tf.concat(grad_flat, 0)return loss_value, grad_flatreturn loss_and_flat_graddef predict(X_star):with tf.device('/GPU:0'):X_star = tf.convert_to_tensor(X_star, dtype=tf.float32)u_star, _ = u_x_model(u_model, X_star[:,0:1], X_star[:,1:2])return u_star.numpy()sizes_w = []
sizes_b = []
with tf.device('/GPU:0'):for q, width in enumerate(layers_sa):if q != 1:sizes_w.append(int(width * layers_sa[1]))sizes_b.append(int(width if q != 0 else layers_sa[1]))###############################################################################
################################ Training Loop ################################
###############################################################################
for i in range(0, number_of_neurons):print("******************************************************************")########################### SA PINN Training ############################ac_sa_train = ac_neurons[i]lmbda, eps  = float(ac_sa_train[0]), float(ac_sa_train[1])col_weights = tf.Variable(tf.random.uniform([N_f, 1]))u_weights   = tf.Variable(100*tf.random.uniform([N0, 1]))#initialize the NNu_model = neural_net(layers_sa)if (i+1 == number_of_neurons):print(f"Begin Final SA-PINN Training: lambda={lmbda}, eps={eps} (Obtaining Neuron {i+1})")else:print(f"Begin SA-PINN Training: lambda={lmbda}, eps={eps} (Obtaining Neuron {i+1})")pinn_train_time_1 = time.perf_counter()sa_losses = fit(x_f, t_f, x0, t0, u0, x_lb, t_lb, x_ub, t_ub, col_weights, u_weights, tf_iter = epochs_adam_sa, newton_iter = epochs_lbfgs_sa, lmbda=lmbda, eps=eps)pinn_train_time_2 = time.perf_counter()print("\nSA-PINN Training Completed")print(f"SA-PINN Training Time: {(pinn_train_time_2-pinn_train_time_1)/3600} Hours")w1 = u_model.layers[0].get_weights()[0].Tw2 = u_model.layers[1].get_weights()[0].Tw3 = u_model.layers[2].get_weights()[0].Tw4 = u_model.layers[3].get_weights()[0].Tw5 = u_model.layers[4].get_weights()[0].Tb1 = u_model.layers[0].get_weights()[1]b2 = u_model.layers[1].get_weights()[1]b3 = u_model.layers[2].get_weights()[1]b4 = u_model.layers[3].get_weights()[1]b5 = u_model.layers[4].get_weights()[1]P_list[i] = P(w1, w2, w3, w4, w5, b1, b2, b3, b4, b5).to(device)print(f"\nCurrent GPT-PINN Depth: [2,{i+1},1]")if (save_data):        path = fr".\Full-PINN-Data (AC)\({ac_sa_train})"if not os.path.exists(path):os.makedirs(path)np.savetxt(fr"{path}\saved_w1.txt", w1.numpy())np.savetxt(fr"{path}\saved_w2.txt", w2.numpy())np.savetxt(fr"{path}\saved_w3.txt", w3.numpy())np.savetxt(fr"{path}\saved_w4.txt", w3.numpy())np.savetxt(fr"{path}\saved_w5.txt", w3.numpy())np.savetxt(fr"{path}\saved_b1.txt", b1.numpy())np.savetxt(fr"{path}\saved_b2.txt", b2.numpy())np.savetxt(fr"{path}\saved_b3.txt", b3.numpy())np.savetxt(fr"{path}\saved_b4.txt", b3.numpy())np.savetxt(fr"{path}\saved_b5.txt", b3.numpy())x_test = xt_test[:,0].view(-1).cpu().detach().numpy()t_test = xt_test[:,1].view(-1).cpu().detach().numpy()X_star = np.hstack((x_test[:,None], t_test[:,None]))u = predict(X_star)np.savetxt(fr"{path}\u_test.txt", u)np.savetxt(fr"{path}\adam_losses.txt",  sa_losses[0])np.savetxt(fr"{path}\lbfgs_losses.txt", sa_losses[1])if (plot_pinn_sol):x_test = xt_test[:,0].view(-1).cpu().detach().numpy()t_test = xt_test[:,1].view(-1).cpu().detach().numpy()X_star = np.hstack((x_test[:,None], t_test[:,None]))u = predict(X_star)AC_plot(t_test, x_test, u, title=fr"SA-PINN Solution $\lambda={lmbda}, \epsilon={eps}$")if (plot_pinn_loss):adam_loss  = sa_losses[0]lbfgs_loss = sa_losses[1]loss_plot(epochs_adam_sa, epochs_lbfgs_sa, adam_loss, lbfgs_loss,title=fr"SA-PINN Losses $\lambda={lmbda}, \epsilon={eps}$")if (i == number_of_neurons-1) and (train_final_gpt == False):break############################ GPT-PINN Training ############################layers_gpt = np.array([2, i+1, 1])P_t, P_xx = autograd_calculations(xt_resid, P_list[i])P_t_term[:,i][:,None]  = P_tP_xx_term[:,i][:,None] = P_xxP_IC_values[:,i][:,None]    = P_list[i](IC_xt)P_BC_values[:,i][:,None]    = P_list[i](BC_xt)P_resid_values[:,i][:,None] = P_list[i](xt_resid)largest_case = 0largest_loss = 0if (i+1 == number_of_neurons):print("\nBegin Final GPT-PINN Training (Largest Loss Training)")else:print(f"\nBegin GPT-PINN Training (Finding Neuron {i+2} / Largest Loss Training)")gpt_train_time_1 = time.perf_counter()for ac_param in ac_training:lmbda, eps = ac_param[0], ac_param[1]if ([lmbda, eps] in ac_neurons):idx = ac_neurons.index([lmbda, eps])c_initial = torch.full((1,i+1), 0.)c_initial[0][idx] = 1.else:c_initial = torch.full((1,i+1), 1/(i+1))Pt_lPxx_eP_term = Pt_lPxx_eP(P_t_term[:,0:i+1], P_xx_term[:,0:i+1], P_resid_values[:,0:i+1], lmbda, eps) GPT_NN = GPT(layers_gpt, lmbda, eps, P_list[0:i+1], c_initial, xt_resid, IC_xt, BC_xt, IC_u, BC_u, f_hat, P_resid_values[:,0:i+1], P_IC_values[:,0:i+1],P_BC_values[:,0:i+1], Pt_lPxx_eP_term[:,0:i+1]).to(device)gpt_losses = gpt_train(GPT_NN, lmbda, eps, xt_resid, IC_xt, BC_xt, IC_u, BC_u,P_resid_values[:,0:i+1], P_IC_values[:,0:i+1], P_BC_values[:,0:i+1], Pt_lPxx_eP_term[:,0:i+1],lr_gpt, epochs_gpt, largest_loss, largest_case)largest_loss = gpt_losses[0]largest_case = gpt_losses[1]gpt_train_time_2 = time.perf_counter()loss_list[i] = largest_lossprint("GPT-PINN Training Completed")print(f"GPT Training Time ({i+1} Neurons): {(gpt_train_time_2-gpt_train_time_1)/3600} Hours")if (i+1 < number_of_neurons):ac_neurons[i+1] = largest_caseprint(f"\nLargest Loss (Using {i+1} Neurons): {largest_loss}")print(f"Parameter Case: {largest_case}")
total_train_time_2 = time.perf_counter()###############################################################################
# Results of largest loss, parameters chosen, and times may vary based on
# the initialization of full PINN and the final loss of the full PINN
print("******************************************************************")
print("*** Full PINN and GPT-PINN Training Complete ***")
print(f"Total Training Time: {(total_train_time_2-total_train_time_1)/3600} Hours\n")
print(f"Final GPT-PINN Depth: {[2,len(P_list),1]}")
print(f"\nActivation Function Parameters: \n{ac_neurons}\n")for j in range(number_of_neurons-1):print(f"Largest Loss of GPT-PINN Depth {[2,j+1,2]}: {loss_list[j]}")
if (train_final_gpt):print(f"Largest Loss of GPT-PINN Depth {[2,j+2,2]}: {loss_list[-1]}")if (plot_largest_loss):plt.figure(dpi=150, figsize=(10,8))if (train_final_gpt):range_end = number_of_neurons + 1list_end  = number_of_neuronselse:range_end = number_of_neurons list_end  = number_of_neurons - 1plt.plot(range(1,range_end), loss_list[:list_end], marker='o', markersize=7, c="k", linewidth=3)plt.grid(True)plt.xlim(1,max(range(1,range_end)))plt.xticks(range(1,range_end))plt.yscale("log") plt.xlabel("Number of Neurons",      fontsize=17.5)plt.ylabel("Largest Loss",           fontsize=17.5)plt.title("GPT-PINN Largest Losses", fontsize=17.5)plt.show()############################### GPT-PINN Testing ############################## 
ac_test = ac_training.tolist()
for i in ac_neurons: if (i in ac_test):ac_test.remove(i)    idx = np.random.choice(len(ac_test), test_cases, replace=False)
ac_test = np.array(ac_test)[idx]print(f"\nBegin GPT-PINN Testing ({len(set(idx.flatten()))} Cases)")I = len(P_list)   
layers_gpt = np.array([2, I, 1])
c_initial  = torch.full((1,I), 1/(I))    total_test_time_1 = time.perf_counter()
incremental_test_times = np.ones(len(ac_test))
cnt = 0for ac_test_param in ac_test:lmbda, eps = ac_test_param[0], ac_test_param[1]Pt_lPxx_eP_term = Pt_lPxx_eP(P_t_term, P_xx_term, P_resid_values, lmbda, eps) GPT_NN = GPT(layers_gpt, lmbda, eps, P_list, c_initial, xt_resid, IC_xt, BC_xt, IC_u, BC_u, f_hat, P_resid_values, P_IC_values,P_BC_values, Pt_lPxx_eP_term).to(device)gpt_losses = gpt_train(GPT_NN, lmbda, eps, xt_resid, IC_xt, BC_xt, IC_u, BC_u,P_resid_values, P_IC_values, P_BC_values, Pt_lPxx_eP_term, lr_gpt, epochs_gpt, testing=True)incremental_test_times[cnt] = (time.perf_counter()-total_test_time_1)/3600cnt += 1#np.savetxt(".\incremental_test_times.txt", incremental_test_times)total_test_time_2 = time.perf_counter()
print("\nGPT-PINN Testing Completed")
print(f"\nTotal Testing Time: {(total_test_time_2-total_test_time_1)/3600} Hours")init_time = (total_train_time_2-total_train_time_1)/3600
test_time = incremental_test_times
line = test_time + init_time
x = range(1,test_time.shape[0]+1)
plt.figure(dpi=150, figsize=(10,8))
plt.plot(x, line, c="k", lw=3.5)
plt.xlabel("Test Case Number", fontsize=22.5)
plt.ylabel("Time (Hours)", fontsize=22.5)
plt.xlim(min(x),max(x))
plt.ylim(min(line),max(line))
xtick = list(range(0,test_cases+1,5))
xtick[0] = 1
plt.xticks(xtick)
plt.grid(True)
plt.show()