添加特征的平方或立方可以改进线性回归模型,其他变换通常也对变换某些特征有用,特别是应用数学函数,比如log、exp、sin等。虽然基于树的模型只关注特征的顺序,但是线性模型和神经网络依赖于每个特征的尺度和分布。如果在特征和目标之间存在非线性关系,那么建模就会变得非常困难,特别是对于回归问题。
log和exp函数可以帮助调节数据的相对比例,从而改进线性模型或神经网络的学习效果。在处理具有周期性模式的数据是,sin和cos函数非常有用。
大部分模型都在每个特征(在回归问题中还包括目标值)大致遵循高斯分布时表现最好,也就是说,每个特征的直方图应该是具有类似于熟悉的“钟形曲线”的形状。使用诸如log和exp之类的变换并不稀奇,但却是实现这一点的简单又有效的方法。
在一中特别常见的情况下,这种变换非常有用,就是处理整数计数数据时。计数数据是指类似于“用户A多长时间登录一次”这样的特征。计数不可能取负值,并且通常遵循特定的统计模式下。
下面使用一个模拟的计数数据集,其性质与在自然状态下能找到的数据集类似,特征全都是整数值,而响应是连续的:
import numpy as nprnd=np.random.RandomState(0)
X_org=rnd.normal(size=(1000,3))
w=rnd.normal(size=3)X=rnd.poisson(10*np.exp(X_org))
y=np.dot(X_org,w)计算每个值出现的次数,看数值的分布情况:
print('每个值出现的次数:{}'.format(np.bincount(X[:,0])))

可以看到,数字2是最常见的,出现了68次,之后数字的出现次数快速下降,但也偶尔有一些比较大的数字出现了2次。
将计数可视化:
bins=np.bincount(X[:,0])
plt.bar(range(len(bins)),bins)
plt.xlabel('数字')
plt.ylabel('数字出现的次数')
plt.show()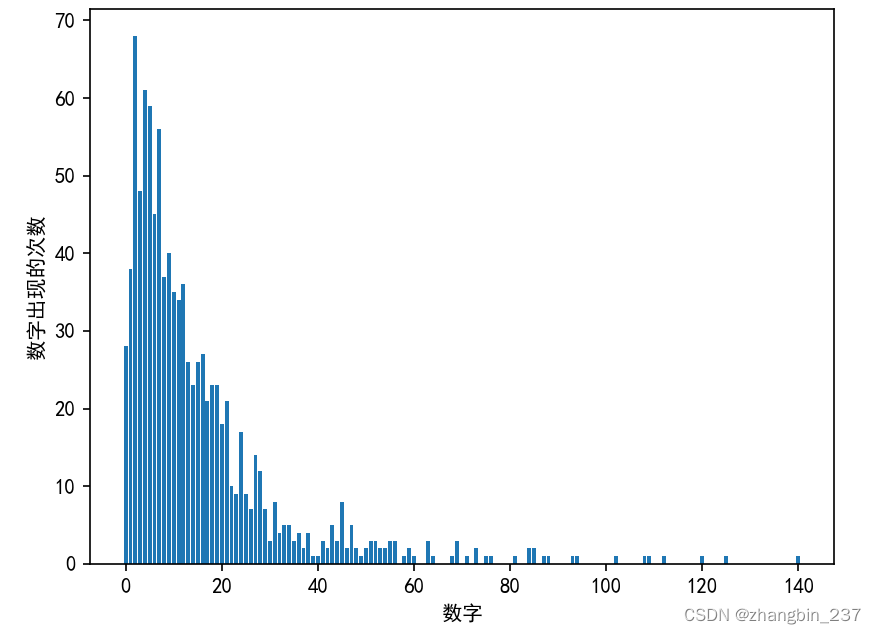
特征X[:,1]和特征X[:,2]具有类似的性质。这种类型的数值分布(许多较小的值和一些非常大的值)在实践中非常常见。但大多数线性模型无法很好地处理这种数据。
尝试拟合一个岭回归模型:
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
score=Ridge().fit(X_train,y_train).score(X_test,y_test)
print('score:{:.3f}'.format(score))
我们可以从相对较小的R*R分数中看出,Ridge无法真正捕捉到X和y之间的关系。不过应用对数变换可能有用。由于数值中包含0,所以我们不能直接应用log,而是要计算log(X+1):
X_train_log=np.log(X_train+1)
X_test_log=np.log(X_test+1)plt.hist(X_train_log[:,0],bins=25)
plt.ylabel('数字出现的次数')
plt.xlabel('数字')
plt.show()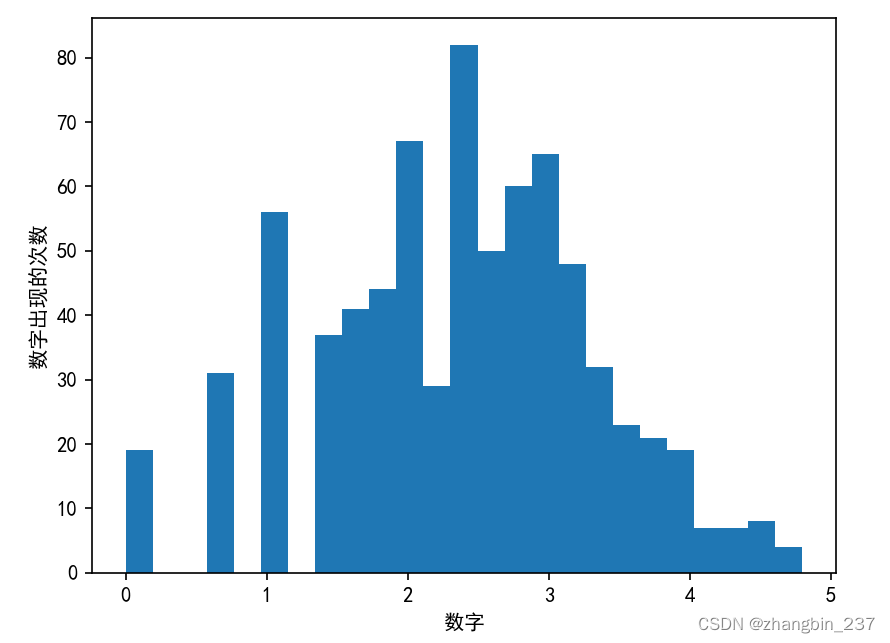
在新数据上构建一个岭回归模型,可以得到更好的拟合:
score=Ridge().fit(X_train_log,y_train).score(X_test_log,y_test)
print('score:{:.3f}'.format(score))
为数据集和模型的所有组合寻找最佳变换,这在某种程度上是一门艺术。在这个例子中,所有的特征都具有相同的性质,这在实践中是非常少见的情况。通常来说,只有一部分特征应该进行变换,有时每个特征的变换方式也各不相同。前面提到过,对基于树的模型而言,这种变换并不重要,但对线性模型来说可能至关重要。
对回归的目标变量y进行变换有时也是一个好主意。尝试预测计数(比如订单数量)是一项相当常见的任务,而且使用log(y+1)变换也往往有用。
从前面的例子中可以看出,分箱、多项式、交互都对模型在给定数据集上的性能有很大的影响,对于复杂度较低的模型更是这样,比如线性模型和朴素贝叶斯模型。与之相反,基于树的模型通常能够自己发现重要的交互项,大多数情况下不需要显式地变换数据。其他模型,比如SVM、最近邻、神经网络,有时可能会从分箱、交互项或多项式中受益,但其效果通常不如线性效果那么明显。













)


)


下源码开发整个流程完成版本(下载->编译->模拟器运行))