二叉树-根据先序遍历和中序遍历序列重建二叉树

一、问题描述

二、解题思路

1.首先明确先序遍历和中序遍历的性质：

2.确定根节点及左右子树

3.对子树进行递归操作

4.递归返回条件

三、代码实现

四、刷题链接

一、问题描述

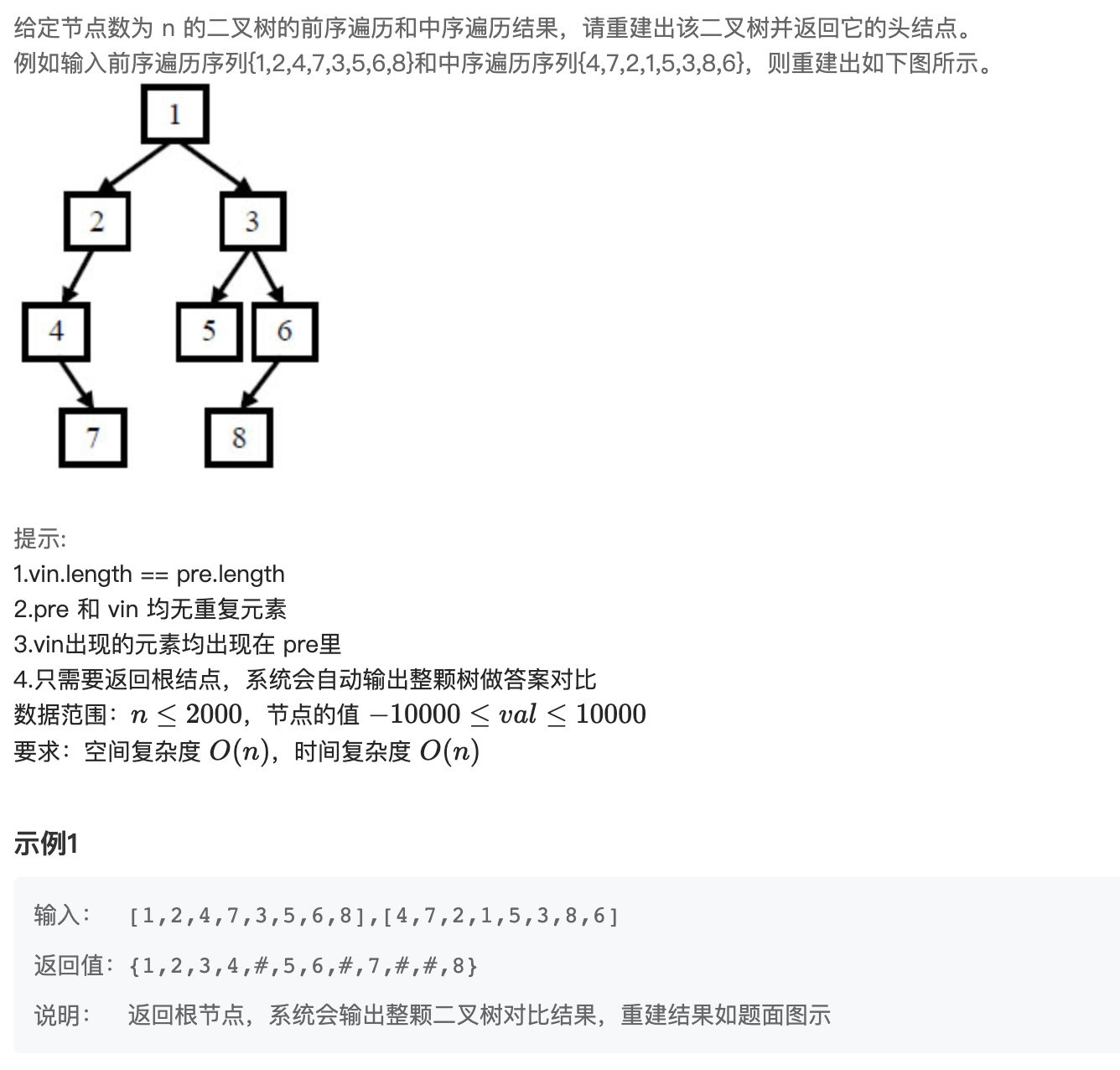
二、解题思路

1.首先明确先序遍历和中序遍历的性质：

先序遍历（根节点、左子树、右子树）

中序遍历（左子树、根节点、右子树）

2.确定根节点及左右子树

第一次递归可以通过先序遍历序列确定根节点元素，然后去中序遍历序列中定位左子树和右子树序列（长度也相应的确定下来），左、右子树在两个序列中的起始位置和终止位置也可以确定下来，目的是对子树再次执行递归操作。

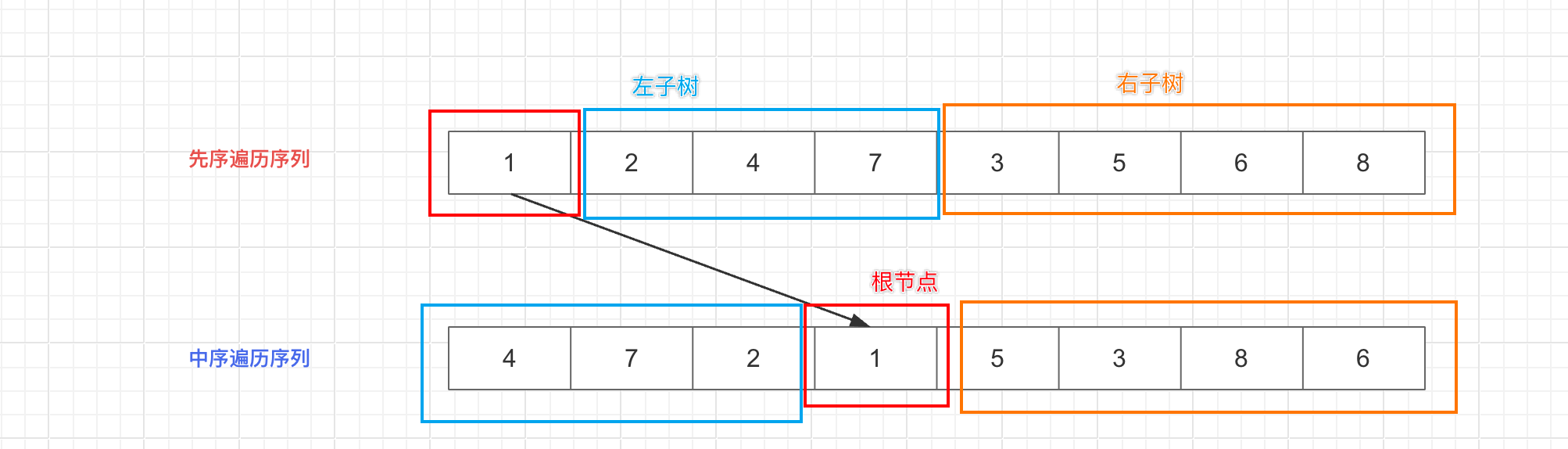
3.对子树进行递归操作

对左子树：先序遍历序列第一个节点（作为左子树的根节点，此时根节点确定）对应中序遍历的最后一个节点，那么证明该左子树没有右子树，只有左子树，再次对左子树执行递归操作。

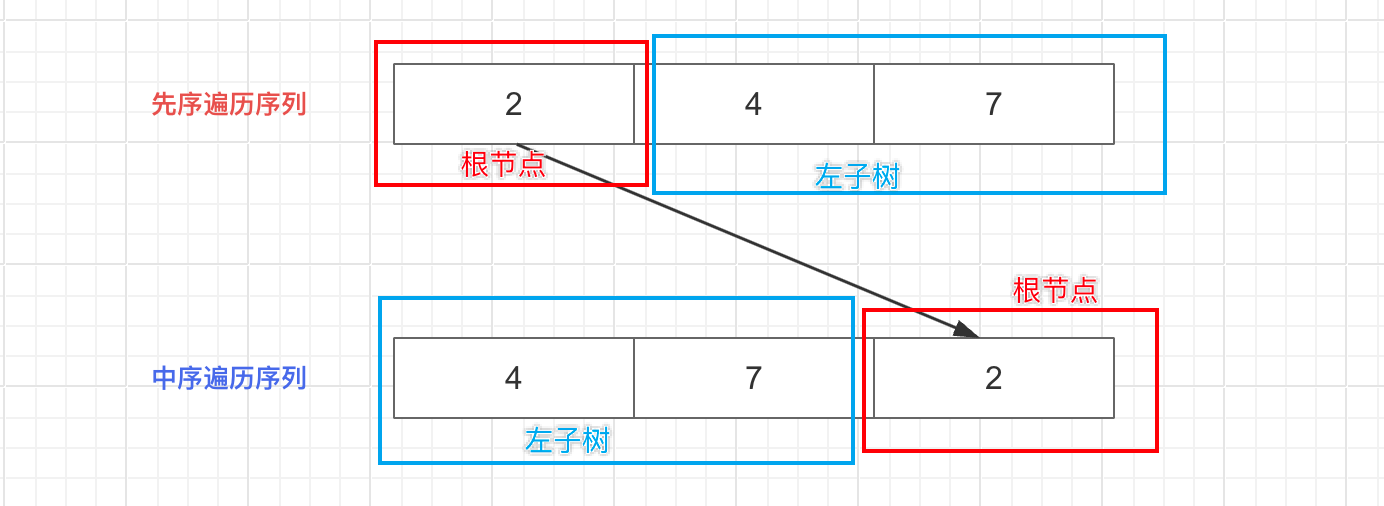
对右子树：先序遍历序列第一个节点（作为右子树的根节点，此时根节点确定），此时根据中序遍历确定本次递归左子树、右子树的起始终止范围，对左、右子树再次执行递归操作。

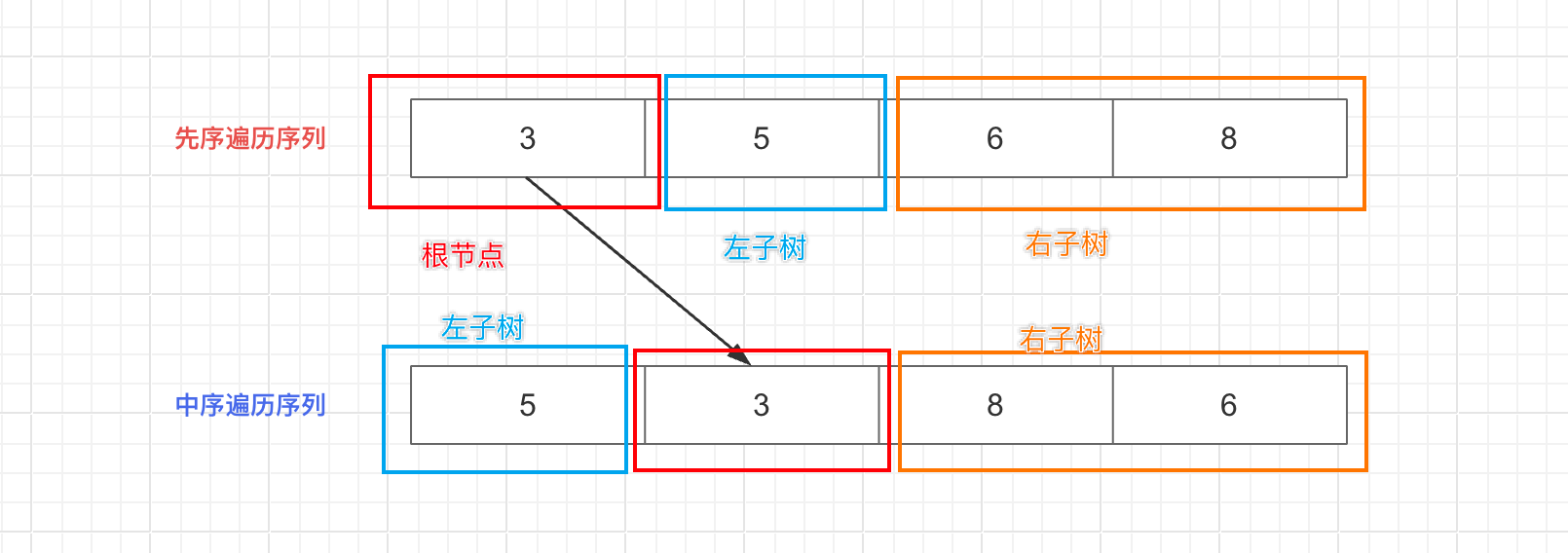
4.递归返回条件

当本次递归只剩一个节点，作为根节点确定下来，递归结束。

三、代码实现

import java.util.*;/** public class TreeNode {*   int val = 0;*   TreeNode left = null;*   TreeNode right = null;*   public TreeNode(int val) {*     this.val = val;*   }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param preOrder int整型一维数组 * @param vinOrder int整型一维数组 * @return TreeNode类*/public TreeNode reConstructBinaryTree (int[] preOrder, int[] vinOrder) {if(preOrder.length==0){return null;}//初始化根节点TreeNode root=new TreeNode(-1);buildTree(preOrder,0,preOrder.length-1,vinOrder,0,vinOrder.length-1,root);return root;}//递归方式构建二叉树public void buildTree(int[] preOrder,int prestart,int preend,int[] vinOrder,int vinstart,int vinend,TreeNode root){int midval=preOrder[prestart];root.val=midval;if(vinstart==vinend){root.left=null;root.right=null;return;}int midvalIdx=vinstart;for(;midvalIdx<=vinend;midvalIdx++){if(vinOrder[midvalIdx]==midval){break;}}int leftsize=midvalIdx-vinstart;int rightsize=vinend-midvalIdx;if(leftsize==0){root.left=null;TreeNode rootright=new TreeNode(-1);root.right=rootright;buildTree(preOrder,prestart+1,preend,vinOrder,midvalIdx+1,vinend,rootright);}else if(rightsize==0){root.right=null;TreeNode rootleft=new TreeNode(-1);root.left=rootleft;buildTree(preOrder,prestart+1,preend,vinOrder,vinstart,midvalIdx-1,rootleft);}else{TreeNode rootleft=new TreeNode(-1);TreeNode rootright=new TreeNode(-1);root.left=rootleft;root.right=rootright;buildTree(preOrder,prestart+1,prestart+leftsize,vinOrder,vinstart,midvalIdx-1,rootleft);buildTree(preOrder,preend-rightsize+1,preend,vinOrder,midvalIdx+1,vinend,rootright);}}
}