条件期望的性质

1.看成f(Y)即可
条件期望仅限于形式化公式,用于解决多个随机变量存在时的期望问题求解,即
E(?)=E(E(?|Y))#直接应用此公式条件住一个随机变量,进行接下来的计算即可
定义随机变量之间的距离为,即均方距离
随机变量的逼近:
使用常数a逼近随机变量,EX为最佳逼近,最佳逼近的误差为Var(X)
Y是已有数据,寻找一个函数g,来让g(Y)逼近X
的解g(Y)=E(X|Y) 即最佳逼近函数即已知数据为条件下的条件期望
频率学派下的统计量(θ为确定参数):
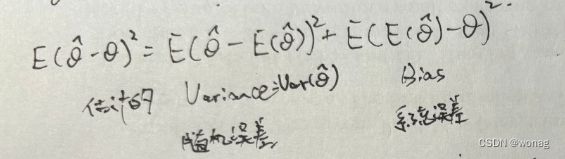
该式为频率学派下的分解,θ为常数,为统计量(
)

Xi为采样的iid随机变量 无偏估计:统计量的期望=欲估计的真值
统计量估计Xi的均值,是无偏估计
统计量估计Xi的方差,也是无偏估计
比较不同的统计量时,在无偏估计的框架下,寻找方差最小的统计量。
充分统计量:给定充分统计量后,随机向量(X1, X2, X3...Xn)的条件分布(将采样的iid样本拼成一个向量)与参数θ无关

找特定分布的充分统计量的方法:nayman分解--瞪眼法看P(X1=x1, X2=x2, ...Xn=xn)找出充分统计量
不同种类的分布都有自己的充分统计量,是个技术活....
充分统计量可以将数据中关于θ的信息全部包含进来,所以找它有啥用?答:保证blockwell方法中的θ'是个统计量,是样本的函数,而与待求参数θ无关(要不然就是耍流氓了,统计量里带θ还估计个p).
改进统计量的方式:rao-blockwell方法,可以降低MSE(前提要求原统计量是无偏的)利用充分统计量

新的统计量θ' 比原统计量好,因为方差降低(他俩都是无偏估计)
完备统计量的定义:T是一个统计量满足 若E(h(T))=0则一定h(T)=0 则称T完备
Lehman-Scheffe定理:假设T是完备且充分的统计量,若h(T)是无偏估计,则h(T)是MVUE估计
cramer-rao下界:计算下界是个技术活
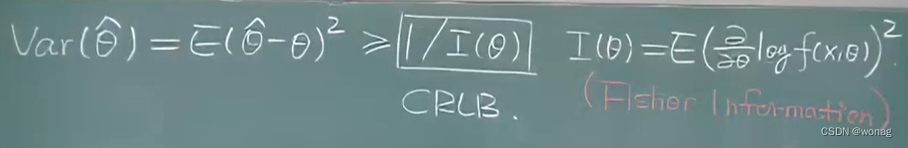
fisher information中的f(x,θ)表示f(X1, X2, X3...,Xn, θ)即随机向量(X1, X2, ..., Xn)的概率密度,在E中xi再看成Xi,对其求期望,于是只剩下成了θ的函数
fisher信息的两种计算方法:

cramerrao下界如果被达到,那么背后的f(x, θ)一定是指数族分布
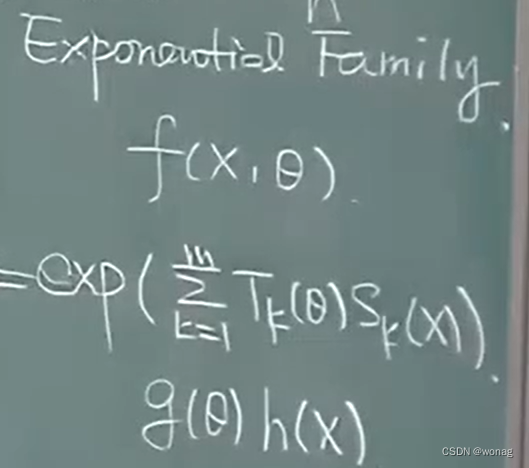
f(x,θ)是指数族分布,则下图式一定是充分完备统计量
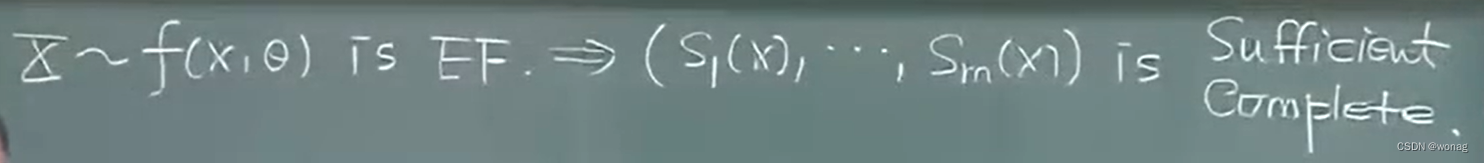
(说明达到cramerrao下界的统计量一定是充分完备统计量,反之不一定)
总结:cramer-rao下界和充分完备统计量有着微妙的联系,揭示了探索MVUE的两种路径的交合处
(整节课都是技术活,关于具体的例子计算可以直接看,作为统计入门)


泽勒一致性是由克里斯汀·泽勒开发的用于计算某天是星期几的算法。)










(进阶))





