题目链接:611.有效三角形的个数
题目描述:
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。

解法一(暴力求解)(会超时):
算法思路:
三层 for 循环枚举出所有的三元组,并且判断是否能构成三角形。
虽然说是暴力求解,但还是想优化一下:
判断三角形的优化:
1.如果能构成三角形,需要满足任意两遍之和要大于第三边。但是实际上只需让较小的两条边之和大于第三边即可。
2.因此我们可以先将原数组排序,然后从小到达枚举三元组,一方面省去枚举的数量,另一方面判断是否能构成三角形
算法代码:
class Solution {
public:int triangleNumber(vector<int>& nums) {//1.排序sort(nums.begin(),nums.end());int n = nums.size(),ret = 0;//2.从小到大枚举所有的三元组for(int i= 0; i< n; i++){for (int j=i+1; j<n; j++) {for(int k = j+1;k<n;k++){// 当最小的两个边之和大于第三边的时候,统计答案if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};解法二(排序+双指针):
算法思路:
先将数组排序
根据「解法一」中的优化思想,我们可以固定一个「最长边」,然后在比这条边小的有序数组中找出一个二元组,使这个二元组之和大于这个最长边。由于数组是有序的,我们可以利用「对撞指针来优化」
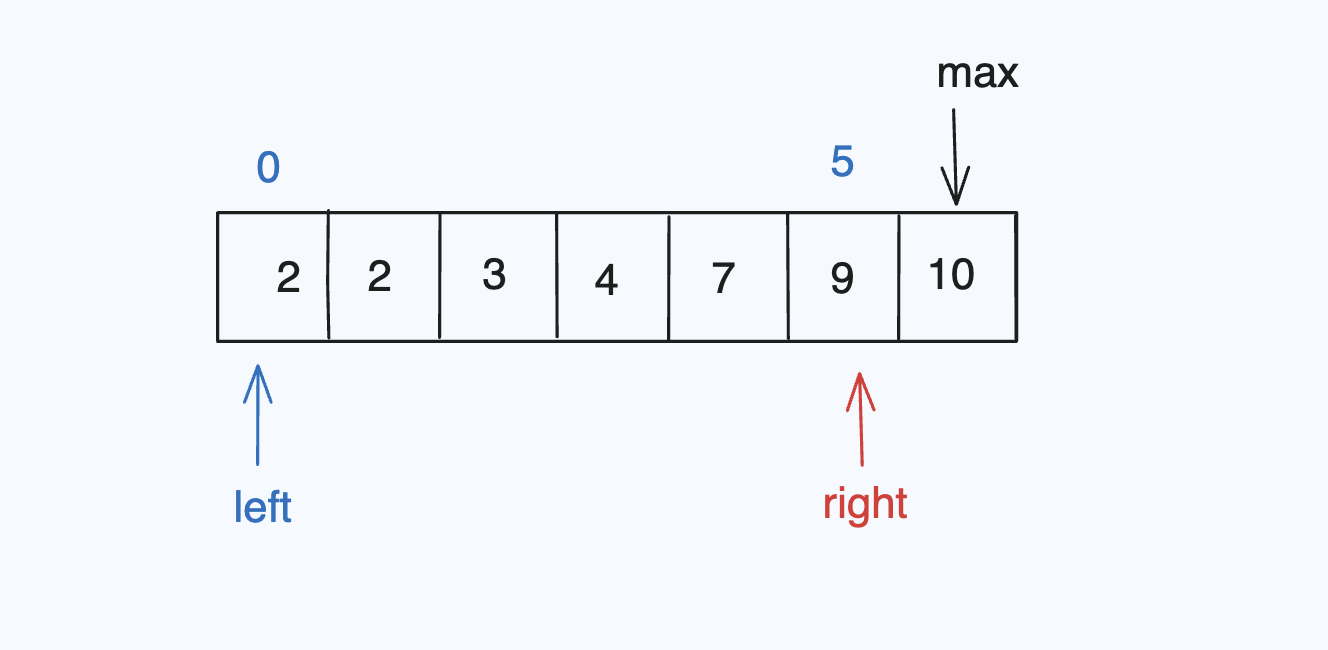
固定一个最长边为max,建立左右指针,由于数组是升序的,那么把右指针放在max前面的位置,接下来通过单调性总结规律。
例如:
2 + 9 > 10(最小的➕次大的数大于最大的数,那么left 与 right之间所有的数与9相加都大于10,也就是有right - left边都满足,此时可以right--)
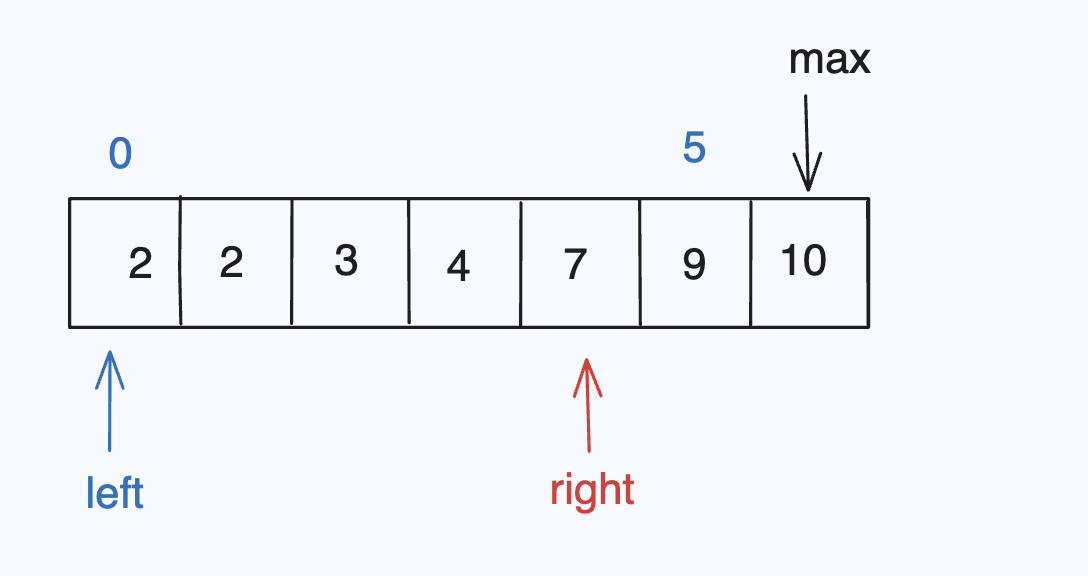
2+7 < 10(最小的与次次大的数相加小于最大数,那么2+2/3/4 都会小于10,因此可以left++)
继续执行循环,直到两指针相遇循环结束
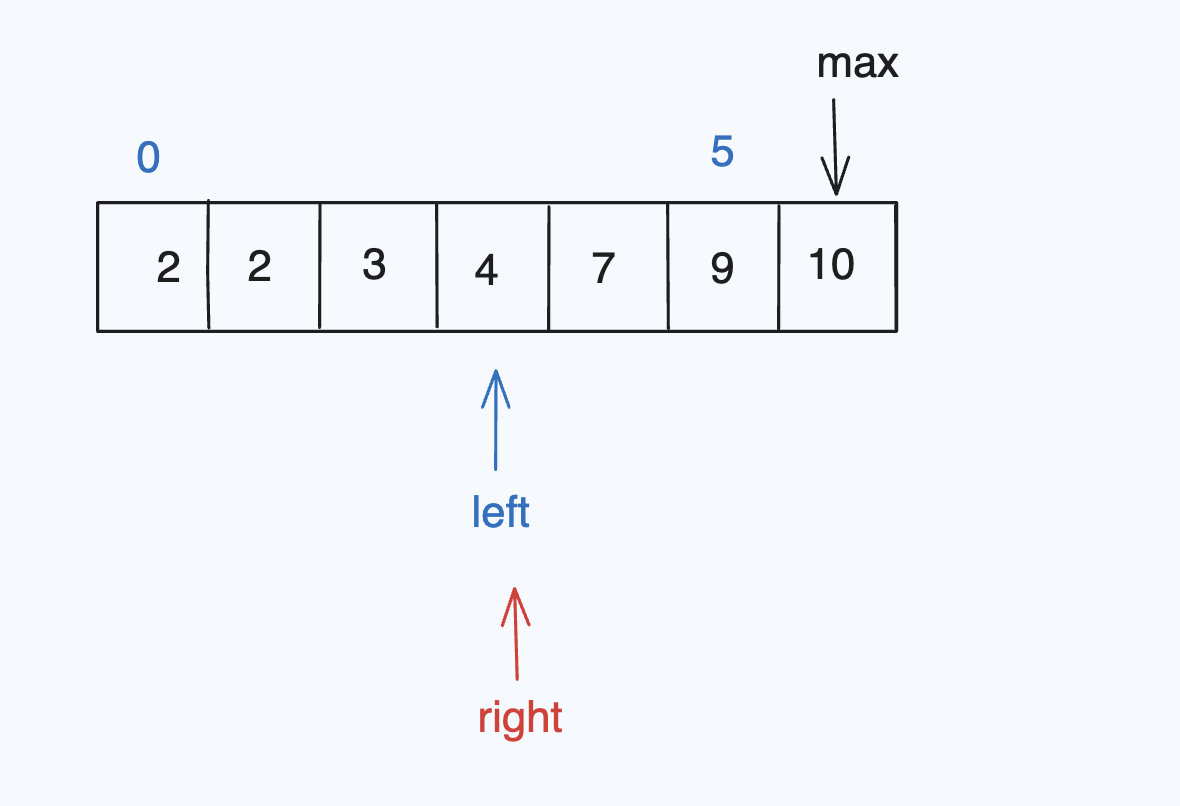
此时,边长为10最大的边情况已经遍历完毕,接下来max--,继续以同样的方式,遍历出每个符合构成三角形的边,累加即可解出此题
class Solution {
public:int triangleNumber(vector<int>& nums) {//数组排序sort(nums.begin(),nums.end());int maxi = nums.size()-1;int max = nums[maxi];int n = 0;//构成三角形最少需要3条边,因此maxi >= 2while(maxi >= 2){int left = 0;int right = maxi-1;while(left != right){if(nums[left] + nums[right] > nums[maxi]){n += right - left;//记录此时满足条件的边的个数的三角形right--;}else{left++;}}maxi--;}return n;}
};)





的读写控制 2)












