本专栏内容为:八大排序汇总 通过本专栏的深入学习,你可以了解并掌握八大排序以及相关的排序算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:八大排序汇总
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

前言:
扑克牌是我们几乎每个人都可能玩过的游戏。最基本的扑克玩法都是一边摸牌,一边理牌。假如我们拿到了这样一手牌,如下图所示。啊,似乎是同花顺呀,别急,我们得理一理顺序才知道是否是真的同花顺。请问,如果是你,应该如何理牌呢?

应该说,哪怕你是第一次玩扑克牌,只要认识这些数字,理牌的方法都是不用教的。将3和4移动到5的左侧,再将2移动到最左侧,顺序就算是理好了。这里,我们的理牌方法,就是直接插入排序法。
直接插入排序
- 直接插入排序算法
- 直接插入排序复杂度分析

直接插入排序算法
直接插入排序(Straight insertion Sort)的基本操作是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增1的有序表。
顾名思义,从名称上也可以知道它是一种插入排序的方法。我们来看直接插入排序法的代码。
注意:排序用到的结构与函数在第一部分:排序的基本概念与分类。我们已经实现。详情请点击:八大排序(一)--------排序的基本概念与分类
void Insertsort(SqList * L)/* 对顺序表L作直接插入排序 */
{int i, j;for (i = 2; i <= L->length; i++){if (L->r[i] < L->r[i - 1])/* 需将L->r[i]插入有序子表 */{L->r[0] = L->r[i];/* 设置哨兵 */for (j = i - 1; L->r[j] > L->r[0]; j--){L->r[j + 1] = L->r[j]; /*记录后移 */}L->r[j + 1] = L->r[0];/* 插入到正确位置 */}}
}
(1)程序开始运行,此时我们传入的SqList参数的值length=6,r[6]={0,5,3,4,6,2},其中r[0]=0将用于后面起到哨兵的作用。
(2)第4~13行就是排序的主循环。i从2开始的意思是我们假设r[1]=5已经放好位置,后面的牌其实就是插入到它的左侧还是右侧的问题。
(3)第6行,此时i2,L.r[i]=3比L.r[i-1]-5要小,因此执行第8~11行的操作。第8行,我们将L.r[0]赋值为L.[i]=3的目的是为了起到第9行和第10行的循环终止的判断依据。如下图所示。图中下方的虚线箭头,就是第10行,L.r[j+1]=L.r[j] 的过程,将5右移一位。
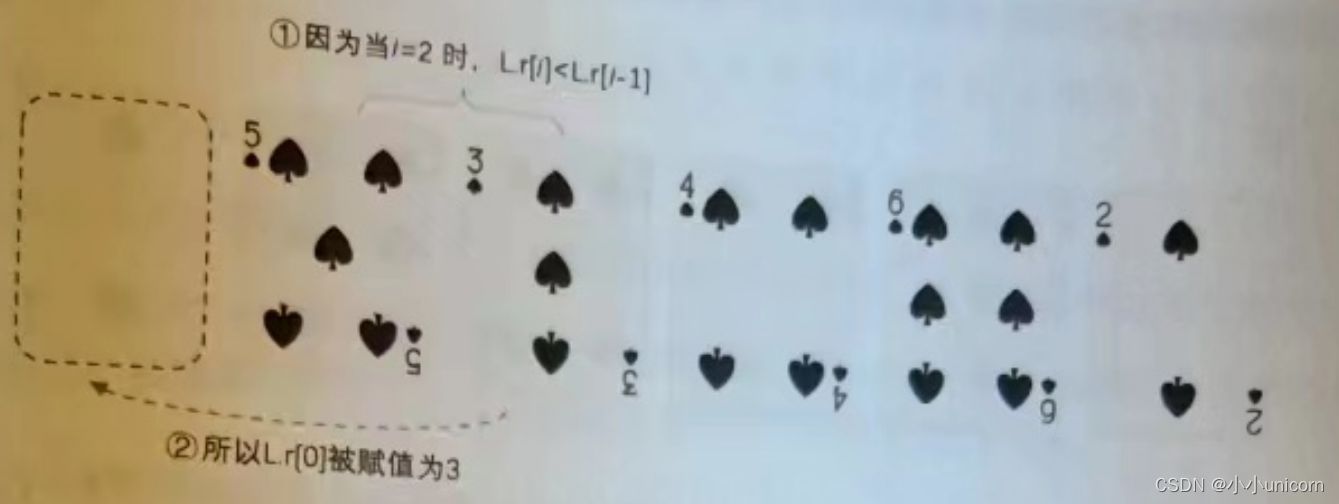
(4)此时,第10行就是在移动完成后,空出了空位,然后第11 行L.r[j+1]=L.r[0],将哨兵的3赋值给-0时的L.r[j+1],也就是说,将扑克牌3放置到L.r[I]的位置,如下图所示。
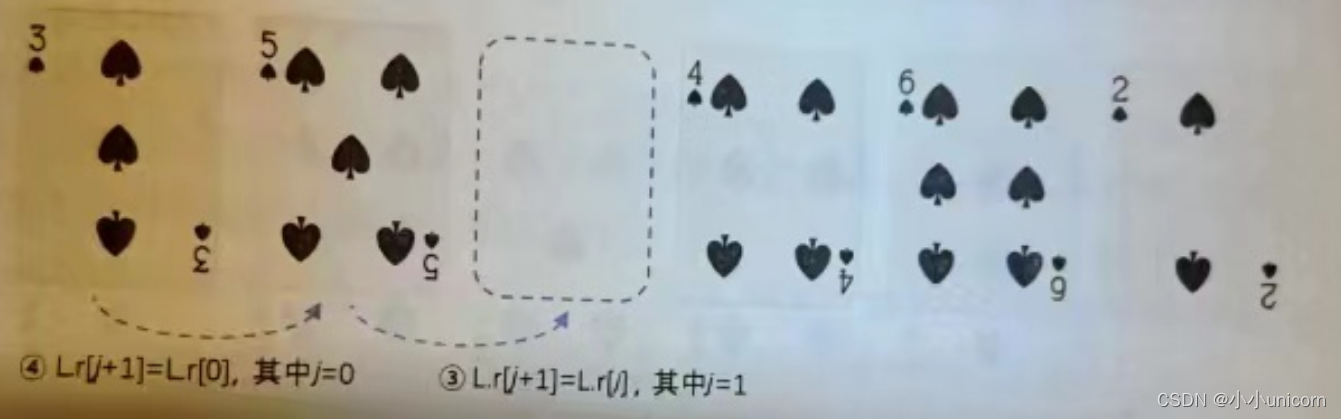
(5)继续循环,第6行,因为此时i=3,L.r[i]=4比L.r[i-1]=5要小,因此执行第8~11行的操作,将5再右移一位,将4放置到当前5所在的位置,如下图所示。

(6)再次循环,此时i4。因为L.r[i]=6比L.r[i-1]=5要大,于是第8~11行代码不执行,此时前三张牌的位置没有变化,如下图所示。

(7)再次循环,此时i=5,因为L.r[i]=2比L.r[i-1]=6要小,因此执行第8~11行的操作。由于6、5、4、3都比2大,它们都将右移一位,将2放置到当前3所在的位置。如下图所示。此时我们的排序也就完成了。

直接插入排序复杂度分析
我们来分析一下这个算法,从空间上来看,它只需要一个记录的辅助空间,因此关键是看它的时间复杂度。
当最好的情况,也就是要排序的表本身就是有序的,比如纸牌拿到后就是{2,3,4,5,6},那么我们比较次数,其实就是代码第6行每个L.r[i]与L.r[i-1]的比较,共比较了(n-1)即( ∑ i = 2 n i \sum_{i=2}^n i ∑i=2ni)次,由于每次都是L.r[i]>L.r[i-1],因此没有移动的记录,时间复杂度为O(n)
当最坏的情况,即待排序表是逆序的情况,比如{6,5,4,3,2),此时需要比较 ∑ i = 2 n = 2 + 3 + . . . + n = ( n + 2 ) ( n − 1 ) / 2 \sum_{i=2}^n =2+3+...+n=(n+2)(n-1)/2 ∑i=2n=2+3+...+n=(n+2)(n−1)/2次,而记录的移动次数也达到最大值 ∑ i = 2 n ( i + 1 ) = ( n + 4 ) ( n − 1 ) / 2 \sum_{i=2}^n (i+1)=(n+4)(n-1)/2 ∑i=2n(i+1)=(n+4)(n−1)/2次。
如果排序记录是随机的,那么根据概率相同的原则,平均比较和移动次数约为n2/4次。因此,我们得出直接插入排序法的时间复杂度为O(n2)。从这里也看出,同样的O(n2)时间复杂度,直接插入排序法比冒泡和简单选择排序的性能要好一些。


)
)








)






