从GAN到WGAN（01/2）

从GAN到WGAN

文章目录

一、说明
二、Kullback-Leibler 和 Jensen-Shannon 背离
三、生成对抗网络（GAN）
四、D 的最优值是多少？
五、什么是全局最优？
六、损失函数代表什么？
七、GAN中的问题

一、说明

生成对抗网络（GAN）在许多生成任务中显示出巨大的效果，以复制现实世界的丰富内容，如图像、人类语言和音乐。它的灵感来自博弈论：两个模型，一个生成器和一个批评家，在相互竞争的同时使彼此更强大。然而，训练GAN模型是相当具有挑战性的，因为人们面临着训练不稳定或收敛失败等问题。

在这里，我想解释一下生成对抗网络框架背后的数学原理，为什么很难训练，最后介绍一个旨在解决训练难点的GAN修改版本。

二、Kullback-Leibler 和 Jensen-Shannon 背离

在我们开始仔细研究 GAN 之前，让我们首先回顾一下用于量化两个概率分布之间相似性的两个指标。

KL（Kullback-Leibler）散度衡量一个概率分布如何偏离第二个预期概率分布
.
$D_{KL}(p \| q) = \int_x p(x) \log \frac{p(x)}{q(x)} dx$

在以下情况下达到最小零点: $p (x) == q (x)$ 处处成立。
该公式表明 KL 散度是不对称的。当 $p (x)$ 接近零而 $q (x)$ 仍然显着大于零时， $q$ 的影响被忽略。当尝试测量两个同等重要的分布之间的相似性时，这可能会导致有问题的结果。

Jensen-Shannon 散度是两个概率分布之间相似性的另一种度量，以.JS发散是对称的（耶！），而且更平滑。如果您有兴趣阅读有关 KL 背离和 JS 背离之间比较的更多信息，请查看这篇 Quora 帖子。
$D_{JS}(p \| q) = \frac{1}{2} D_{KL}(p \| \frac{p + q}{2}) + \frac{1}{2} D_{KL}(q \| \frac{p + q}{2})$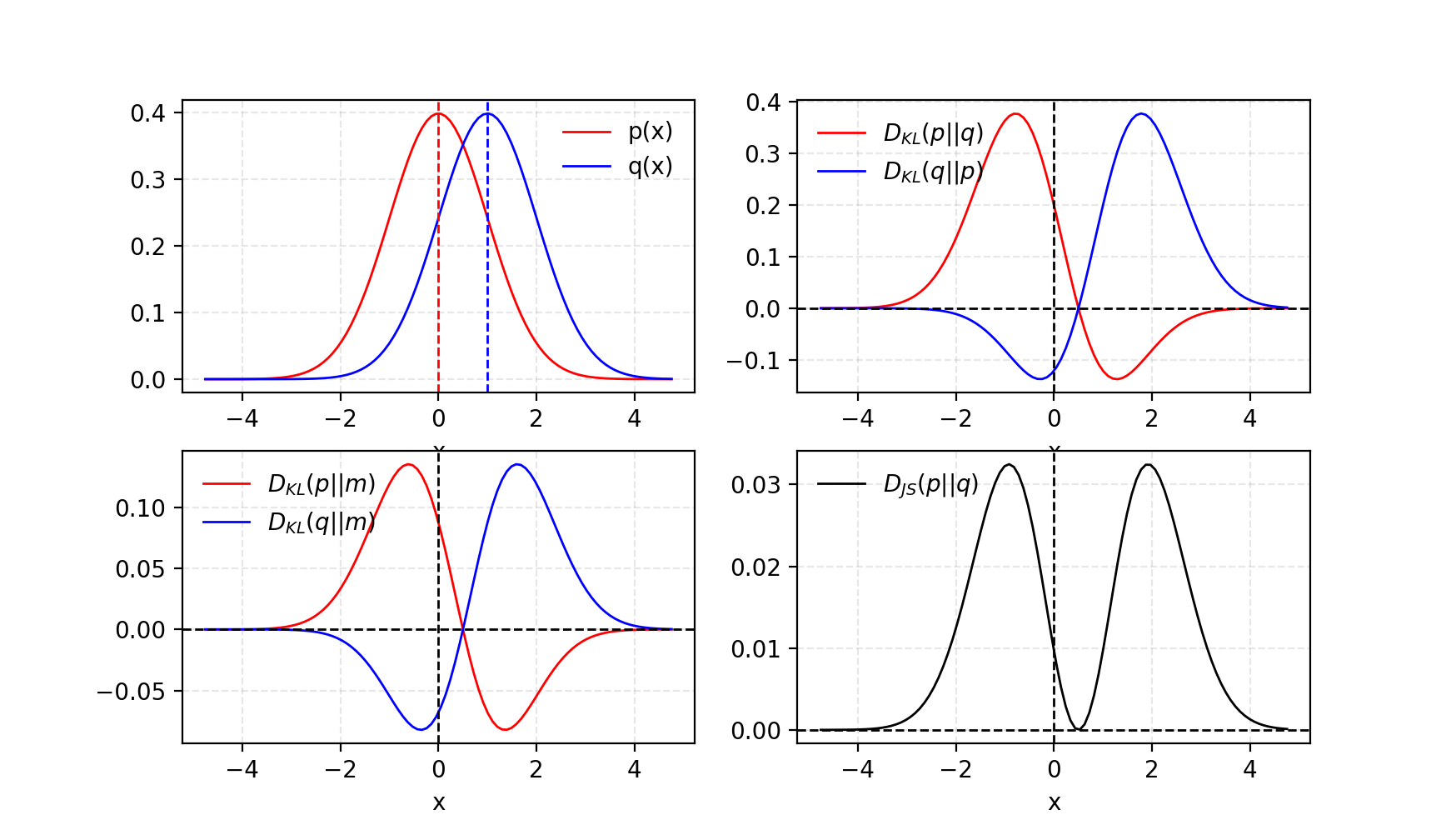
图 1.给定两个高斯分布，平均值=0 且 std=1 且平均值=1，标准度=1。两个分布的平均值标记为.吉隆坡背离是不对称的，但 JS 发散是对称的。

一些人认为（Huszar，2015）GANs取得巨大成功背后的一个原因是将损失函数从传统最大似然方法中的非对称KL散度转换为对称JS散度。我们将在下一节中详细讨论这一点。

三、生成对抗网络（GAN）

GAN由两个模型组成：

鉴别器：估计给定样本来自真实数据集的概率。它作为评论家工作，并经过优化以区分假样品和真样品。
生成器：输出给定噪声变量输入的合成样本 (带来潜在的产出多样性）。它被训练为捕获真实的数据分布，以便其生成样本尽可能真实，或者换句话说，可以欺骗鉴别器提供高概率。

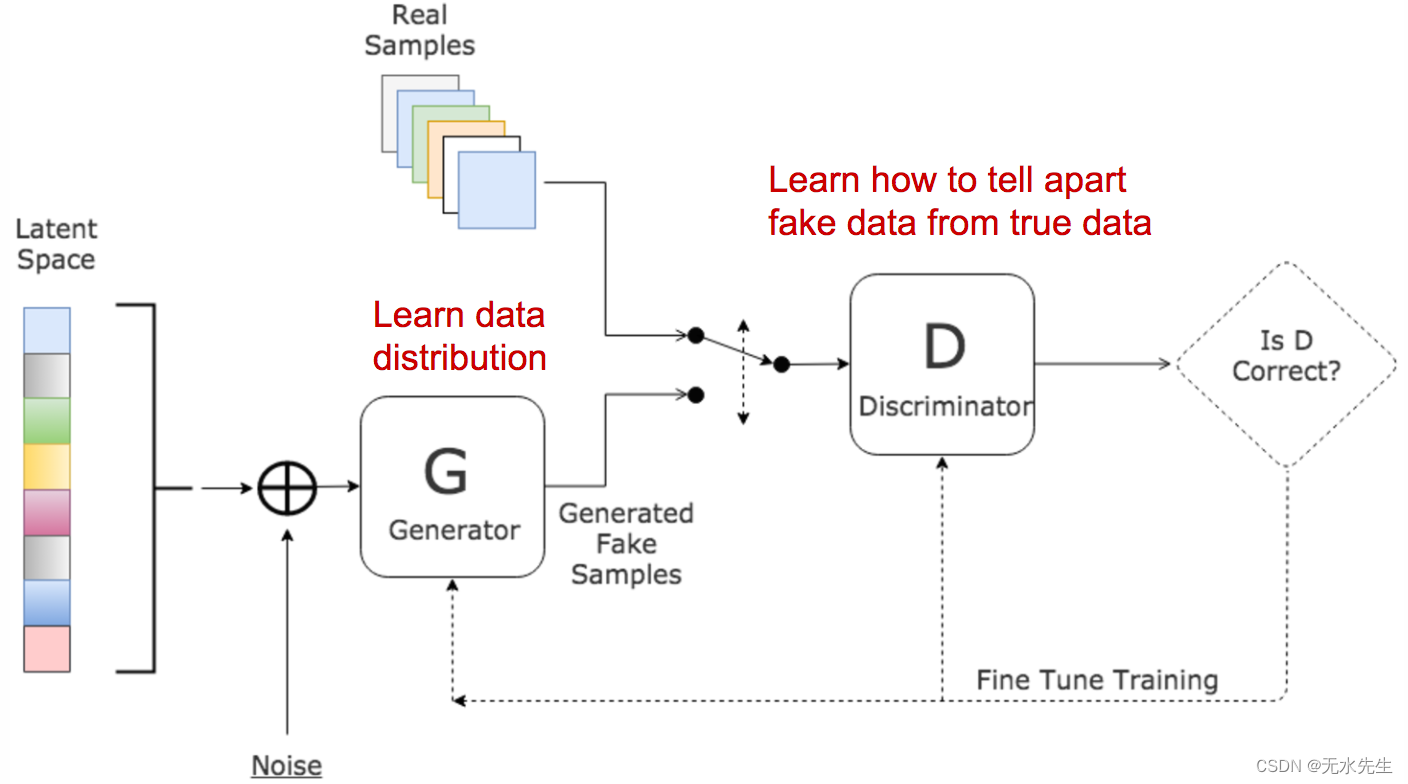
图 2.生成对抗网络的架构。（图片来源：www.kdnuggets.com/2017/01/generative-…-learning.html)
这两个模型在训练过程中相互竞争：生成器在努力欺骗鉴别者，而批评者模型
正在努力不被骗。两种模型之间这种有趣的零和博弈激励了两者改进其功能。

鉴于

Symbol	Meaning	Notes
$p_z$	Data distribution over noise input z	Usually, just uniform.
$p_g$	The generator’s distribution over data x
$p_r$	Data distribution over real sample x

一方面，我们的目标是通过最大化 $\mathbb{E}_{x \sim p_{r}(x)} [\log D(x)]$ 来确保判别器 $D$ 对真实数据做出准确的决策。另一方面，对于假样本 $\sim p_z(z)$ ，判别器应该输出一个接近于零的概率 $D (G (z))$ ，这是通过最大化 $\mathbb{E}_{z \sim p_{z}(z)} [\log (1 - D(G(z)))]$ 。
另一方面，生成器经过训练以增强 $D$ 为虚假示例分配高概率的可能性，从而最小化 $\mathbb{E}_{z \sim p_{z}(z)} [\log (1 - D(G(z)))]$ 。
当整合这两个方面时，D 和 G 进行极小极大博弈，其目标是优化后续损失函数：
$\begin{aligned} \min_G \max_D L(D, G) & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log(1 - D(G(z)))] \\ & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{x \sim p_g(x)} [\log(1 - D(x)] \end{aligned}$
$\mathbb{E}_{x \sim p_{r}(x)} [\log D(x)]$ 在梯度下降更新期间对 G 没有影响。

四、D 的最优值是多少？

现在我们有一个明确定义的损失函数。让我们首先检查一下什么是D最佳值
.
$\int_x \bigg( p_{r}(x) \log(D(x)) + p_g (x) \log(1 - D(x)) \bigg) dx$

由于我们感兴趣的是确定 D(x) 的最佳值以最大化 L(G,D)，因此我们将贴上标签
$\tilde{x} = D(x), A=p_{r}(x), B=p_g(x)$
然后是积分内部的东西（我们可以安全地忽略积分，因为对所有可能的值进行采样）为：
$\begin{aligned} f(\tilde{x}) & = A log\tilde{x} + B log(1-\tilde{x}) \\ \frac{d f(\tilde{x})}{d \tilde{x}} & = A \frac{1}{ln10} \frac{1}{\tilde{x}} - B \frac{1}{ln10} \frac{1}{1 - \tilde{x}} \\ & = \frac{1}{ln10} (\frac{A}{\tilde{x}} - \frac{B}{1-\tilde{x}}) \\ & = \frac{1}{ln10} \frac{A - (A + B)\tilde{x}}{\tilde{x} (1 - \tilde{x})} \\ \end{aligned}$

因此，设置 $\frac{d f(\tilde{x})}{d \tilde{x}} = 0$ ，我们得到鉴别器的最佳值：

$D^*(x) = \tilde{x}^* = \frac{A}{A + B} = \frac{p_{r}(x)}{p_{r}(x) + p_g(x)} \in [0, 1]$
.
Once the generator is trained to its optimal,
$p_g$ gets very close to $p_r$ . When $p_g = p_{r}$ , $D^*(x)$ becomes 1/2.
.

一旦生成器被训练到最佳状态， $p_g$ 非常接近 $p_r$ 。当 $p_g = p_{r}$ 时， $D^*(x)$ 变为1/2。

五、什么是全局最优？

当两者都G和D处于最佳值，我们有 $p_g = p_{r}$ 和 $D^*(x)=1/2$ 。损失函数变为：

$\begin{aligned} L(G, D^*) &= \int_x \bigg( p_{r}(x) \log(D^*(x)) + p_g (x) \log(1 - D^*(x)) \bigg) dx \\ &= \log \frac{1}{2} \int_x p_{r}(x) dx + \log \frac{1}{2} \int_x p_g(x) dx \\ &= -2\log2 \end{aligned}$

六、损失函数代表什么？

根据上一节中列出的公式，JS 之间的背离 $p_g$ 和 $p_r$ ，可以计算为：
$\begin{aligned} D_{JS}(p_{r} \| p_g) =& \frac{1}{2} D_{KL}(p_{r} || \frac{p_{r} + p_g}{2}) + \frac{1}{2} D_{KL}(p_{g} || \frac{p_{r} + p_g}{2}) \\ =& \frac{1}{2} \bigg( \log2 + \int_x p_{r}(x) \log \frac{p_{r}(x)}{p_{r} + p_g(x)} dx \bigg) + \\& \frac{1}{2} \bigg( \log2 + \int_x p_g(x) \log \frac{p_g(x)}{p_{r} + p_g(x)} dx \bigg) \\ =& \frac{1}{2} \bigg( \log4 + L(G, D^*) \bigg) \end{aligned}$

因此 $L(G, D^*) = 2D_{JS}(p_{r} \| p_g) - 2\log2$
当判别器最优时，生成对抗网络 (GAN) 的损失函数使用 Jensen-Shannon 散度来衡量生成的数据分布 $p_g$ 与真实样本分布 $p_r$ 之间的相似性。最优生成器 $G^*$ 复制真实数据分布，导致最小损失 $L(G^*, D^*) = -2\log2$ ，与前面的方程一致。