上一篇写过了用单一最近邻分类器训练后的精度只有0.22.

现在用PCA。想要度量人脸的相似度，计算原始像素空间中的距离是一种相当糟糕的方法。用像素表示来比较两张图像时，我们比较的是每个像素的灰度值与另一张图像对应位置的像素灰度值。这种表示与人们对人脸图像的解释方式有很大不同，使用这种原始表示很难获取到面部特征。例如，如果使用像素距离，那么将人脸向右移动一个像素将发生巨大变化，得到一个完全不同的表示。我们希望，使用沿着主成分方向的距离可以提高精度。这里我们启用PCA的白化选项，它将主成分缩放到相同的尺度提高精度。变换后的结果与使用StandardScaler相同。白化不仅对应旋转数据，还对应于缩放数据时期形状是圆形而不是椭圆形：

mglearn.plots.plot_pca_whitening()
plt.show()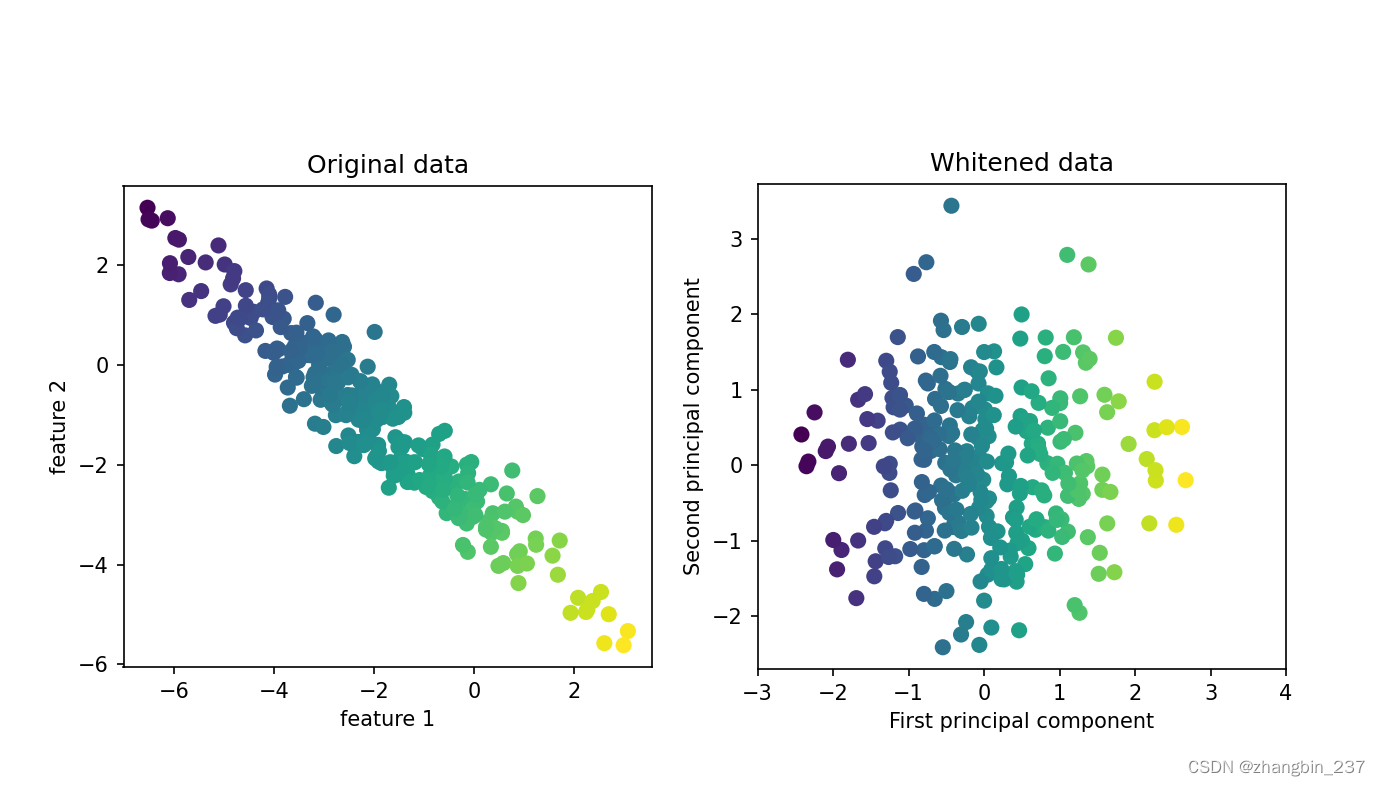

我们对训练数据拟合PCA对象，并提取前100个主成分，然后对训练数据和测试数据进行变换。

pca=PCA(n_components=100,whiten=True,random_state=0).fit(X_train)
X_train_pca=pca.transform(X_train)
X_test_pca=pca.transform(X_test)print('X_train_pca.shape:{}'.format(X_train_pca.shape))

新数据有100个特征，即前100个主成分。现在，对新表示使用单一最近邻分类器来将新图像分类：

knn=KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca,y_train)
print('test set accuracy:{:.2f}'.format(knn.score(X_test_pca,y_test)))

可以看到精度有显著提升。这证实了我们的直觉，即主成分可能提供了一种更好的数据表示。

对于图像数据，我们还很容易地将找到的主成分可视化。成分对应于输入空间里的方向。这里的输入空间是87*65像素的灰度像素，所以这个空间中的方向也是87*65像素的灰度图像。

先看一下前几个主成分：

print('pca.components_.shape:{}'.format(pca.components_.shape))

fig,axes=plt.subplots(3,5,figsize=(15,12),subplot_kw={'xticks':(),'yticks':()})
for i,(components,ax) in enumerate(zip(pca.components_,axes.ravel())):ax.imshow(components.reshape(image_shape),cmap='viridis')ax.set_title('{}.components'.format((i+1)))
plt.show()

虽然我们肯定无法理解这些成分的所有内容，但可以猜测一些主成分捕捉到了人脸图像的哪些方面。第一个主成分似乎主要编码的是人脸与背景 的对比，第二个主成分编码的是人脸左半部分和右半部分的明暗程度差异，如此等等。虽然这种表示比原始像素值的语义稍强，但它仍与人们感知人脸的方式相去甚远。由于PCA模型是基于像素的，因此人脸的相对位置和明暗程度都对两张图像在像素表示中的相似程度有很大影响。但人脸的相对位置和明暗程度可能并不是人们首先感知的内容。在要求人们评价人脸的相似度时，它们更可能会使用年龄、性别、表情、发型等属性，而这些属性很难从像素强度中推断出来。重要的是要记住，算法对数据（特别是视觉数据）的解释通常与人类的解释方式不同。

回到PCA的具体案例。我们对PCA变换的介绍是：先旋转数据，然后删除方差较小的成分。另一种有用的解释是：尝试找到一些数字（PCA旋转后的新特征值），使我们可以将测试点表示为主成分的加权求和。

我们还可以用另一种方法来理解PCA模型，就是仅使用一些成分对原始数据进行重建。我们可以对人脸做类似的变换，将数据酱味道只包含一些主成分，然后反向旋转到原始空间。回到原始特征空间可以通过inverse_transform方法来实现。

分别利用10、50、100、500个成分对一些人脸进行重建并将其可视化：

mglearn.plots.plot_pca_faces(X_train,X_test,image_shape)
plt.show()

从结果上可以看到，在仅使用10个主成分时，进捕捉到图片的基本特点，比如人脸方向和明暗程度。随着使用的主成分越来越多，图像中也保留了越来越多的细节。如果使用的成分个数与像素个数相同，意味着我们旋转后不会丢弃任何信息，可以完美重建图像。

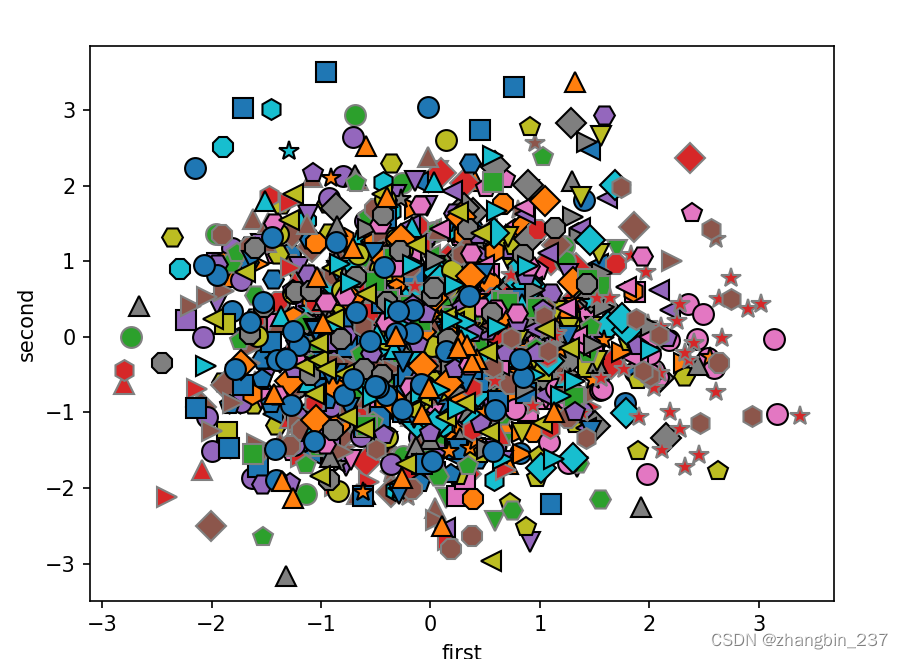
还可以尝试用PCA的前两个主成分，将数据集中所有人脸在散点图中可视化，其类别在图中给出，这与我们对cancer数据集所做的类似：

mglearn.discrete_scatter(X_train_pca[:,0],X_train_pca[:,1],y_train)
plt.xlabel('first')
plt.ylabel('second')
plt.show()