每日一题——Python实现PAT甲级1077 Kuchiguse（举一反三+思想解读+逐步优化）


一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

我的写法

代码点评

时间复杂度分析

空间复杂度分析

总结

我要更强

方案1：利用字典树（后缀树）

优化代码（后缀树实现）

代码点评

时间复杂度分析

空间复杂度分析

方案2：水平扫描法

优化代码（水平扫描法实现）

代码点评

时间复杂度分析

空间复杂度分析

总结

哲学和编程思想

1. 字典树（Trie）方法

编程思想

哲学理念

2. 水平扫描法

编程思想

哲学理念

3. 动态编程（不在上述代码中，但也是常见的优化方法）

编程思想

哲学理念

总结

举一反三

1. 数据结构优化

2. 空间换时间

3. 递归与迭代

4. 分而治之

5. 贪心算法

6. 动态规划

总结



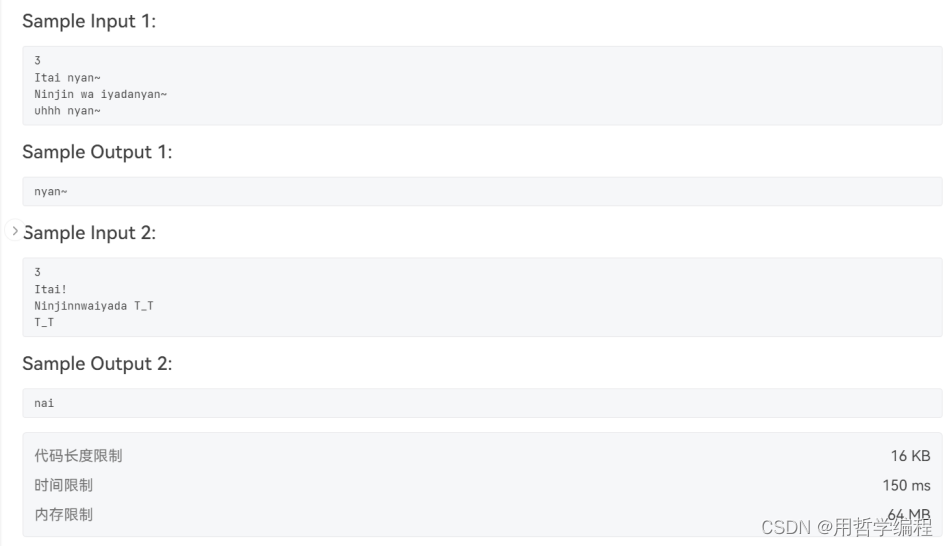
题目链接

我的写法

N=int(input())  # 读取一个整数N，表示有多少个字符串
strs=[]  # 创建一个空列表来存储字符串
for i in range(N):  # 循环N次strs.append(input()[::-1])  # 读取每个字符串并将其倒序，然后添加到列表strs中same_end=''  # 初始化一个空字符串，用于存储相同的后缀
for i in range(min([len(s) for s in strs])):  # 找出所有字符串中最短的长度，并遍历该长度if len(set([strs[j][i] for j in range(N)]))==1:  # 检查所有字符串在第i个位置上的字符是否相同same_end+=strs[0][i]  # 如果相同，则将该字符添加到same_end中else:  # 如果不相同break  # 结束循环if len(same_end)==0:  # 如果没有相同的后缀print("nai")  # 输出"nai"
else:  # 如果有相同的后缀print(same_end[::-1])  # 将same_end倒序输出，即得到原始的相同后缀

这段代码的功能是找到多个字符串的最长公共后缀。以下是对代码的专业点评以及时间复杂度和空间复杂度分析：

代码点评

  1. 输入处理：
    • 使用 input() 读取输入的整数 N，然后读取 N 个字符串，并将其倒序存储在列表 strs 中。这样做是为了方便从后向前逐字符比较字符串。
  2. 查找公共后缀：
    • 首先计算所有字符串的最小长度，确保不会越界。
    • 逐字符检查所有字符串在当前位是否相同，如果相同则添加到 same_end 中，否则终止检查。
  3. 结果输出：
  • 如果 same_end 为空，则输出 "nai"，表示没有公共后缀。
  • 否则将 same_end 倒序输出，即为原始字符串的公共后缀。

时间复杂度分析

因此，查找公共后缀部分的总体时间复杂度为 O(M * N)。

  1. 输入处理：
    • 读取 N 个字符串的时间复杂度是 O(N)。
    • 每个字符串的倒序操作的时间复杂度是 O(L)，其中 L 是字符串的平均长度。总体时间复杂度为 O(N * L)。
  2. 查找公共后缀：
    • 计算最小长度的时间复杂度是 O(N)。
    • 逐字符比较的时间复杂度是 O(M * N)，其中 M 是最短字符串的长度。
  3. 结果输出：
  • 输出的时间复杂度为 O(M)。

综合以上分析，总的时间复杂度为 O(N * L + M * N)，在最坏情况下 L 和 M 都可以接近最长字符串长度。

空间复杂度分析

  1. 输入处理：
    • 使用了一个列表 strs 来存储 N 个字符串，空间复杂度为 O(N * L)。
  2. 查找公共后缀：
  • 使用了一个字符串 same_end 来存储公共后缀，最坏情况的空间复杂度为 O(M)。

综合分析，空间复杂度为 O(N * L + M)。

总结

这段代码在处理字符串公共后缀问题时较为直接，逻辑清晰，步骤明确。代码的时间复杂度和空间复杂度都取决于输入字符串的数量和长度，但对于常规的输入规模，性能表现应该是合理的。优化的重点可以放在减少字符串操作的次数和改进字符串比较过程。

我要更强

在寻找多个字符串的最长公共后缀时，时间复杂度和空间复杂度的优化可以通过多种途径实现，例如避免多余的字符串操作，使用更高效的数据结构等。以下是一些可能的优化方案，并给出相应的代码和注释：

方案1：利用字典树（后缀树）

字典树（Trie）是一种高效的数据结构，特别适合字符串集合的共性处理。在这里，可以使用反向构建的后缀树来查找公共后缀。

优化代码（后缀树实现）

class TrieNode:def __init__(self):self.children = {}self.is_end_of_word = Falseclass Trie:def __init__(self):self.root = TrieNode()def insert(self, word):current = self.rootfor char in word:if char not in current.children:current.children[char] = TrieNode()current = current.children[char]current.is_end_of_word = Truedef longest_common_suffix(self, n):common_suffix = []current = self.rootwhile len(current.children) == 1 and not current.is_end_of_word:(char, next_node), = current.children.items()common_suffix.append(char)current = next_noden -= 1if n == 0:breakreturn ''.join(common_suffix)def find_longest_common_suffix(strings):trie = Trie()for string in strings:trie.insert(string[::-1])return trie.longest_common_suffix(len(strings))N = int(input())  # 读取一个整数N，表示有多少个字符串
strs = [input() for _ in range(N)]  # 读取N个字符串result = find_longest_common_suffix(strs)if not result:print("nai")
else:print(result[::-1])

代码点评

  1. Trie 数据结构：
    • 使用 TrieNode 类表示字典树的节点。
    • 使用 Trie 类封装字典树的插入和寻找最长公共后缀的功能。
  2. 插入字符串：
    • 将每个字符串倒序后插入字典树。
  3. 寻找公共后缀：
  • 在字典树中搜索最长的路径，路径上的字符即为最长公共后缀。

时间复杂度分析

  • 插入每个字符串的时间复杂度为 O(L)，其中 L 是字符串的长度，因此总插入时间复杂度为 O(N * L)。
  • 寻找最长公共后缀的时间复杂度为 O(M)，其中 M 是最短字符串的长度。

综合时间复杂度为 O(N * L)。

空间复杂度分析

  • 字典树节点的空间复杂度为 O(N * L)，因为每个字符都可能需要一个节点。
  • 另外，存储结果的空间复杂度为 O(M)。

综合空间复杂度为 O(N * L)。

方案2：水平扫描法

水平扫描法通过逐一比较字符串，类似于前缀匹配，但是从字符串末尾开始。

优化代码（水平扫描法实现）

def find_longest_common_suffix(strings):if not strings:return ""# 取第一个字符串作为基准suffix = strings[0][::-1]# 逐个比较其他字符串for string in strings[1:]:temp_suffix = ""rev_string = string[::-1]min_length = min(len(suffix), len(rev_string))# 从后向前比较字符for i in range(min_length):if suffix[i] == rev_string[i]:temp_suffix += suffix[i]else:breaksuffix = temp_suffixif not suffix:breakreturn suffixN = int(input())  # 读取一个整数N，表示有多少个字符串
strs = [input() for _ in range(N)]  # 读取N个字符串result = find_longest_common_suffix(strs)if not result:print("nai")
else:print(result[::-1])

代码点评

  1. 水平扫描：
    • 使用第一个字符串作为初始公共后缀的基准。
    • 逐一与后续字符串进行比较，更新公共后缀。
  2. 字符比较：
  • 从后向前逐字符比较，直到找到不同字符或达到最短长度。

时间复杂度分析

  • 比较每个字符串的时间复杂度为 O(M)，其中 M 是最短字符串的长度。因此总时间复杂度为 O(N * M)。

空间复杂度分析

  • 存储公共后缀的空间复杂度为 O(M)。

综合空间复杂度为 O(M)。

总结

上述优化方法在时间和空间复杂度上相比原始方案都有一定的提升。字典树（后缀树）方法在处理大量字符串时更高效，而水平扫描法实现简单且易于理解。选择哪种方法可以根据具体的应用场景和性能需求来定。

哲学和编程思想

在优化寻找多个字符串的最长公共后缀的方法时，涉及到一些重要的编程思想和哲学理念。以下是对这些思想的详细说明：

1. 字典树（Trie）方法

编程思想
  • 数据结构优化：字典树是一种特定的树结构，专门用于处理字符串集合，通过将公共前缀合并在一起，可以高效地存储和查询字符串。
  • 空间换时间：字典树在插入和查询时，花费的时间与字符串的长度呈线性关系，因此可以通过增加空间复杂度来降低时间复杂度。
  • 递归与迭代：字典树的构建和查询通常使用递归或迭代的方式来遍历各节点。
哲学理念
  • 分而治之：将问题分解为更小的子问题，通过处理这些子问题来解决整个问题。字典树通过逐层处理每个字符，实现了这一思想。
  • 高效存储与快速访问：字典树在设计上就是为了优化字符串的存储和访问，这反映了在计算机科学中追求效率的哲学理念。

2. 水平扫描法

编程思想
  • 贪心算法：每次选择当前最优的解，在这里，每次比较当前字符串的最长公共后缀并更新。
  • 迭代优化：逐步改进解决方案，通过不断迭代来优化结果。
  • 暴力搜索：尽管是优化的暴力搜索，水平扫描法还是采用了一种直接比较的方式，这是一种简单且直接的思维方式。
哲学理念
  • 最小工作原则：每一步都尽量少做工作，只比较必要的字符。这种方法避免了多余的计算和复杂的逻辑。
  • 逐步求精：通过逐步比较和更新公共后缀，从而逐渐接近最终解决方案。这种逐步优化的思想在哲学上类似于“渐进主义”。

3. 动态编程（不在上述代码中，但也是常见的优化方法）

编程思想
  • 子问题重用：将问题分解为子问题，通过记忆化或表格存储中间结果，避免重复计算。
  • 状态转移：通过状态转移方程来确定从一个状态到另一个状态的关系。
哲学理念
  • 整体与部分：整体问题的解决依赖于部分问题的解决，通过解决部分问题，逐步构建整体解决方案。
  • 平衡与优化：动态规划在时间和空间之间找到平衡，通过空间换时间来优化计算过程。

总结

通过使用不同的数据结构和算法优化，不仅提高了程序的效率，还展示了重要的编程思想和哲学理念。这些方法在计算机科学中都有广泛的应用，体现了在解决问题时对效率、简洁性和可维护性的追求。字典树方法体现了分而治之和高效存储的哲学，而水平扫描法则展示了逐步求精和贪心算法的思想。这些方法的结合，使得可以更好地理解和处理复杂的字符串问题。

举一反三

理解和应用编程思想与哲学理念，可以帮助在遇到各种编程问题时，灵活地找出高效的解决方案。以下是一些技巧，能帮助举一反三，从而更好地应对各种复杂问题：

1. 数据结构优化

技巧：

  • 学习和理解常用的数据结构（如数组、链表、栈、队列、树、图、哈希表等）的特点和适用场景。
  • 在解决问题时，首先考虑是否有合适的数据结构能简化问题或提高效率。
  • 对于特定的应用场景，考虑定制或组合多种数据结构。

举例：

  • 当处理大量字符串时，考虑使用字典树（Trie）来高效地存储和查询公共前缀或后缀。
  • 在频繁需要插入和删除操作时，选择链表而不是数组。

2. 空间换时间

技巧：

  • 当计算时间复杂度较高时，考虑使用额外的空间来存储中间结果，从而减少计算时间。
  • 使用缓存或者记忆化技术（如动态规划中的 memoization）来避免重复计算。

举例：

  • 在动态规划中，使用二维数组存储中间计算结果，优化递归问题的时间复杂度。
  • 在查找问题中，使用哈希表存储已访问节点或结果，优化查找速度。

3. 递归与迭代

技巧：

  • 理解递归和迭代的转换，当递归深度过大时尝试使用迭代来避免栈溢出。
  • 递归适用于分治法，迭代适用于需要多次重复计算的场景。

举例：

  • 使用递归实现快速排序（Quick Sort），但在递归深度可能过大时，改为使用迭代版本。
  • 通过迭代实现斐波那契数列，避免递归重复计算。

4. 分而治之

技巧：

  • 将复杂问题划分为更小的子问题，分别解决这些子问题再合并结果。
  • 使用分治法处理递归问题或大数据量的处理问题。

举例：

  • 使用归并排序（Merge Sort）将大问题拆分成小问题，再合并排序。
  • 在二分搜索中，将问题空间逐步缩小，直到找到目标。

5. 贪心算法

技巧：

  • 每一步选择当前最好（最优）的解，适用于局部最优能导致全局最优的问题。
  • 贪心算法往往简单高效，但需证明所选策略能得到全局最优解。

举例：

  • 在活动选择问题中，每次选择结束时间最早的活动。
  • 在找零问题中，每次选择面值最大的硬币。

6. 动态规划

技巧：

  • 识别问题的子结构，将问题分解为子问题，通过存储子问题的解来避免重复计算。
  • 使用表格法或记忆化技术存储子问题的解，优化计算过程。

举例：

  • 在背包问题中，使用二维数组存储每个容量和物品组合的最优解。
  • 在最长公共子序列问题中，构建二维表格来存储子序列的长度。

总结

通过灵活运用数据结构优化、空间换时间、递归与迭代、分而治之、贪心算法和动态规划等编程思想，可以更高效地解决各种复杂问题。在面对新的问题时，尝试识别其性质，寻找合适的编程思想和数据结构，从而设计出高效的解决方案。多练习和多思考，将这些技巧内化为自己的编程习惯，就能举一反三，游刃有余地解决各种编程挑战。

感谢支持。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/850499.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

CloudFlare 防火墙规则里开放合法 Bot 爬虫的方法

CloudFlare 防火墙规则里开放合法 Bot 爬虫的方法

明月使用 CloudFlare 也算是有一阵子了，可以说效果非常好更是非常满意，毕竟每天成千上万的 Web 攻击和 cc 攻击都能控制在几乎可以忽略不计的程度了，上次因调试需要关闭了国内线路上的网站卫士统计图覆对比就很能说明这点儿： 这是关闭防火墙当天的实时防御统计结果 这是开启…
阅读更多...
刘强东的拼搏哲学与产品创新的启示

刘强东的拼搏哲学与产品创新的启示

在当今这个快速变化的时代，成功不再是偶然，而是需要一种敢于挑战、敢于拼搏的精神。正如京东创始人刘强东所说：“实现梦想，记住这句话就够了。敢于挑战，敢于拼搏的人不一定能成功，但成功的人一定是敢于挑战…
阅读更多...
unity3d：GameFramework+xLua+Protobuf+lua-protobuf，生成.cs,.pb工具流

unity3d：GameFramework+xLua+Protobuf+lua-protobuf，生成.cs,.pb工具流

概述 1.区分lua，cs用的proto 2.proto生成cs，使用protogen.exe，通过csharp.xslt修改生成cs样式 3.proto生成lua加载.pb二进制文件，并生成.pb列表文件，用于初始化加载 4.协议id生成cs，lua中枚举 区分cs&…
阅读更多...
Splashtop正式入驻长三角（杭州）制造业数字化能力中心，赋能企业向数字化转型

Splashtop正式入驻长三角（杭州）制造业数字化能力中心，赋能企业向数字化转型

2024年6月，Splashtop正式入驻长三角（杭州）制造业数字化能力中心。作为全球领先的远程桌面控制软件供应商，Splashtop致力于提供适用于远程办公、IT 和 MSP 远程支持等多场景的高性能远程桌面控制软件和解决方案，赋能企业…
阅读更多...
Qt之QGraphicsView —— 笔记3：矩形图元连接（附完整源码）

Qt之QGraphicsView —— 笔记3：矩形图元连接（附完整源码）

效果 完整源码 注意：在ui文件中拖入一个QGraphicsView类窗口控件，然后用MyGraphicsView提升该类。 main.cpp #include "widget.h" #include <QApplication>int main(
阅读更多...
SpringBoot+Vue学生宿舍管理系统（前后端分离）

SpringBoot+Vue学生宿舍管理系统（前后端分离）

技术栈 JavaSpringBootMavenMySQLMyBatisVueShiroElement-UI 角色对应功能 学生宿管员管理员 功能截图
阅读更多...
基于非下采样小波包分析的滚动轴承故障诊断（MATLAB R2021B）

基于非下采样小波包分析的滚动轴承故障诊断（MATLAB R2021B）

小波变换具有良好的时频局部化特性和多分辨率特性&#xff0c;可准确定位信号的突变点并可在不同尺度上描述信号的局部细节特征&#xff0c;被广泛应用于信号降噪。但标准正交小波变换不具有平移不变性&#xff0c;采用标准正交小波对信号消噪后&#xff0c;会在脉冲尖峰处产生…
阅读更多...
Polar Web【简单】PHP反序列化初试

Polar Web【简单】PHP反序列化初试

Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境&#xff0c;显示下图中的PHP代码&#xff0c;于是展开分析&#xff1a; 首先发现Easy类中有魔术函数 __wakeup() &#xff0c;实现的是对成员…
阅读更多...
VisionPro的应用和入门教程

VisionPro的应用和入门教程

第1章 关于VisionPro 1.1 康耐视的核心技术 1. 先进的视觉系统 康耐视的视觉系统结合了高性能的图像传感器、复杂的算法和强大的计算能力&#xff0c;能够实时捕捉、分析和处理高分辨率图像。其视觉系统包括固定式和手持式两种&#xff0c;适用于各种工业环境。无论是精密电…
阅读更多...
[经验] 场效应管是如何发挥作用的 #知识分享#学习方法#职场发展

[经验] 场效应管是如何发挥作用的 #知识分享#学习方法#职场发展

场效应管是如何发挥作用的 在现代电子技术领域&#xff0c;场效应管&#xff08;MOSFET&#xff09;是一种重要的半导体元器件。它的作用非常广泛&#xff0c;例如在集成电路中扮演着关键的角色。在本文中&#xff0c;我们将详细探讨场效应管的作用及其在实际应用中的意义。 简…
阅读更多...
SpringBoot+Vue企业客户管理系统（前后端分离）

SpringBoot+Vue企业客户管理系统（前后端分离）

技术栈 JavaSpringBootMavenMySQLMyBatisVueShiroElement-UI 角色对应功能 员工管理员 功能截图
阅读更多...
git根据历史某次提交创建新分支

git根据历史某次提交创建新分支

有时候项目在做版本管理的时候&#xff0c;忘记了创建某次版本的分支&#xff0c;而直接在主分支上进行开发了&#xff0c;这个时候&#xff0c;想要对某次提交单独拉出来一个版本分支&#xff0c;就需要用到这个功能&#xff1a; git checkout -b 新分支名 某次提交的id 找到…
阅读更多...
LLM技术

LLM技术

LLM 是利用深度学习和大数据训练的人工智能系统&#xff0c;专门设计来理解、生成和回应自然语言。这些模型通过分析大量的文本数据来学习语言的结构和用法&#xff0c;从而能够执行各种语言相关任务。以 GPT 系列为代表&#xff0c;LLM 以其在自然语言处理领域的卓越表现&…
阅读更多...
53.ReentrantLock原理

53.ReentrantLock原理

ReentrantLock使用 ReentrantLock 实现了Lock接口&#xff0c; 内置了Sync同步器继承了AbstractQueuedSynchronizer。 Sync是抽象类&#xff0c;有两个实现NonfairSync非公平&#xff0c;FairSync公平。 所以ReentrantLock有公平锁和非公平锁。默认是非公平锁。 public sta…
阅读更多...
线性预测器的等价性

线性预测器的等价性

摘要 尽管线性模型很简单&#xff0c;但它在时间序列预测中表现良好&#xff0c;即使是在与更深入、更昂贵的模型竞争时也是如此。已经提出了许多线性模型的变体&#xff0c;通常包括某种形式的特征归一化&#xff0c;以提高模型的泛化。本文分析了用这些线性模型体系结构可表…
阅读更多...
Mysql使用中的性能优化——索引数对插入操作性能的影响

Mysql使用中的性能优化——索引数对插入操作性能的影响

表的索引可以给数据检索提升效率&#xff0c;但是也给表的增删改操作带来代价。本文我们将关注&#xff0c;索引数量对INSERT操作的影响。 结论 索引数的新增会造成INSERT操作效率下降&#xff0c;约每增一个索引会降低10%效率。 实验数据 可以看到0个索引的效率是7个索引效…
阅读更多...
【C++题解】1265. 爱因斯坦的数学题

【C++题解】1265. 爱因斯坦的数学题

问题&#xff1a;1265. 爱因斯坦的数学题 类型&#xff1a;简单循环 题目描述&#xff1a; 爱因斯坦出了一道这样的数学题&#xff1a;有一条长阶梯&#xff0c;若每步跨 2 阶&#xff0c;则最最后剩一阶&#xff0c;若每步跨 3 阶&#xff0c;则最后剩 2 阶&#xff0c;若每…
阅读更多...
分布式事务大揭秘：使用MQ实现最终一致性

分布式事务大揭秘：使用MQ实现最终一致性

本文作者：小米，一个热爱技术分享的29岁程序员。如果你喜欢我的文章，欢迎关注我的微信公众号“软件求生”，获取更多技术干货！ 大家好，我是小米，一个热爱分享技术的29岁程序员，今天我们来聊聊分布式事务中的一种经典实现方式——MQ最终一致性。这是一个在互联网公司中广…
阅读更多...
Wow Tab插件，一款能让你的Edge浏览器开挂的插件，微软官方出品

Wow Tab插件，一款能让你的Edge浏览器开挂的插件，微软官方出品

首先问你个问题&#xff0c;你的浏览器起始页是什么样的界面&#xff1f;是默认的界面还是极简的界面&#xff1f;又或者是既简洁又功能丰富的新型起始页呢&#xff1f;如果你的起始页是浏览器默认的&#xff0c;从来都没有更改过的话&#xff0c;建议你可以尝试一些第三方的起…
阅读更多...
6.切蛋糕

6.切蛋糕

上海市计算机学会竞赛平台 | YACSYACS 是由上海市计算机学会于2019年发起的活动，旨在激发青少年对学习人工智能与算法设计的热情与兴趣，提升青少年科学素养，引导青少年投身创新发现和科研实践活动。https://www.iai.sh.cn/problem/71 题目描述 一个圆型的蛋糕，切 𝑛n 刀…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023