目录
一、交叉列联表和卡方检验的关系
(一)什么是交叉列联表
(二)什么是卡方检验
(三)除了卡方检验,列联表分析还可以结合其他统计方法
二、列联表只能用于两个分类变量吗?
三、卡方检验:统计量与P值的协同作用及应用指南
卡方检验中的卡方统计量和P值的作用:
四、列联表和卡方检验实例
(一)数据收集
(二)列联表构造
(三)卡方检验步骤
Step1:建立原假设
Step2:计算期望频数/理论频数:
Step3:计算卡方统计量:
编辑
Step4:确定自由度:
Step5:查χ2方分布临界值表,确定接受域
在卡方检验中,确定P值通常有以下几种方法:
五、Python实现交叉列联分析和卡方检验
(一)导入库
(二)输入列联表数据
(三)使用chi2_contingency函数执行卡方检验
(四)输出卡方统计量
(五)输出P值
(六) 输出自由度
(七) 输出理论频数
一、交叉列联表和卡方检验的关系
(一)什么是交叉列联表
交叉列联表是一种统计表格,用于展示两个或多个分类变量之间的频数分布情况。它通过将变量的不同类别交叉组合,形成一个表格,其中每个单元格表示相应类别的组合出现的频数。
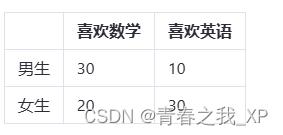
例如,假设我们有一个关于学生性别和喜欢的学科的调查数据:男生中有30人喜欢数学,10人喜欢英语;女生中有20人喜欢数学,30人喜欢英语。我们可以将这些数据整理成一个交叉列联表,如下所示:
(二)什么是卡方检验
卡方检验是一种统计方法,用于检验两个分类变量之间是否独立。它通过比较观察频数和期望频数之间的差异来判断变量之间是否存在关联。
在交叉列联表中,我们可以使用卡方检验来分析变量之间的关系。例如,在上面的例子中,我们可以使用卡方检验来检验学生的性别是否与他们喜欢的学科有关。
(三)除了卡方检验,列联表分析还可以结合其他统计方法
- 费舍尔精确检验(Fisher's Exact Test):适用于样本量较小的情况,当样本量较大时,其结果与卡方检验相似。
- 列联系数(如Phi系数、Cramer's V系数):用于衡量变量之间的关联强度。
- 修正的卡方检验或Yates' continuity correction:用于处理某些特殊情况下的数据偏差。
- 多维度扩展分析:对多个变量进行Log-linear模型分析,探索变量间的复杂关系和相互作用模式。
二、列联表只能用于两个分类变量吗?
虽然列联表最基础的形式是用于展示两个分类变量之间的频数分布情况,但这并不意味着它仅限于两个变量。列联表同样可以扩展以分析多个分类变量之间的关系,这种情况下通常称为多维列联表或多路列联表。
在多维列联表中,表格会有更多的维度,用来表示三个或三个以上变量的交叉分类。例如,如果你正在分析学生的学科成绩(优秀、良好、及格、不及格)、性别(男、女)以及是否参加过辅导班(是、否)之间的关系,那么就需要一个三维列联表来呈现这些变量的所有可能组合及其频数分布。
多维列联表可能会更加复杂,难以直接可视化,因此在分析时可能需要借助特定的统计软件来进行汇总和解释,也可能需要应用更高级的统计方法,如对多个变量进行的log-linear模型分析,来探索变量间的复杂关系和相互作用模式。
三、卡方检验:统计量与P值的协同作用及应用指南
卡方检验中的卡方统计量通常指计算得出的测试统计值,而P值则代表在原假设为真的条件下,观察到的统计量或更极端情况的概率。在实际应用中,两者都非常重要,但通常以P值作为判断假设是否成立的最终标准。
卡方检验中的卡方统计量和P值的作用:
1. 卡方统计量的计算与意义
- 卡方统计量是通过比较观察频数与理论频数之间的差异来计算的。
- 它反映了数据与预期模式之间的偏离程度。
- 卡方值越大,表明观察数据与理论预期的差异越大,进而说明原假设可能不成立。2. P值的获取与解释
- P值是依据卡方统计量、数据的自由度以及预设的显著性水平(通常为0.05)来获取的[。
- P值小,意味着在原假设成立的条件下,出现当前结果或更极端情形的概率低,因此有理由拒绝原假设。
- 相反,P值较大时,没有足够证据拒绝原假设,从而认为数据与预期模式相符。3. P值的确定:
- 根据卡方统计量和相应的自由度,查找卡方分布表或使用统计软件得到P值。
- P值表示在原假设成立的情况下,观察到当前卡方统计量或更极端情况的概率。4. 结论推断:
- 如果P值小于或等于显著性水平(通常为0.05),则拒绝原假设,认为分类变量之间存在显著关系。
- 如果P值大于显著性水平,则没有足够证据拒绝原假设,认为分类变量之间无显著关系。综上所述,卡方统计量提供了量化的数据变异性大小,而P值给出了这种变异性是否具有统计学意义的概率解释。两者共同构成了完整的卡方检验流程,协助研究者做出更准确的统计推断。在具体应用时,应结合研究目的和数据特性选择合适的检验方法,并正确解读卡方统计量与P值,以便得出科学合理的结论。
四、列联表和卡方检验实例
让我们通过一个详细的实例来理解列联表和卡方检验的应用。假设我们想要探究大学生的专业选择(文科 vs. 理科)与其性别(男 vs. 女)之间是否存在关联。这是一个典型的定类变量间关系的研究问题,非常适合使用列联表和卡方检验。
(一)数据收集
(二)列联表构造
(三)卡方检验步骤
Step1:建立原假设
- 零假设 (H0): 学生的性别与其专业选择之间是相互独立的,即性别不影响专业选择。
- 备择假设 (H1): 学生的性别与其专业选择之间存在关联。
Step2:计算期望频数/理论频数:
对于每个单元格,根据行总和与列总和计算如果两个变量完全独立时该单元格应有的频数。
在这个表格中,我同时展示了:
- 每个格子左上角的实际观察频数(最初提供的数据);
- 每个格子右下角的计算出的期望频数(基于假设变量间独立的理论值)。
这样的展示方式有助于直观对比实际数据与理论期望之间的差异,进而进行卡方检验分析,判断这些差异是否具有统计学意义。
Step3:计算卡方统计量:
计算得出的卡方统计量(χ²)大约为0.646。
Step4:确定自由度:
对于2x2表,自由度 = (行数 - 1) * (列数 - 1) = (2-1)*(2-1) = 1。
Step5:查χ2方分布临界值表,确定接受域
假设显著性水平a取0.05
使用卡方分布表来确定P值。根据计算的卡方统计量(χ²)和确定自由度(df),得到p值为0.818,0.42>0.05,则P值大于显著性水平,则没有足够证据拒绝原假设,认为分类变量之间无显著关系,即学生的性别与其专业选择之间是相互独立的,即性别不影响专业选择。
在卡方检验中,确定P值通常有以下几种方法:
查表法:
- 使用卡方分布表来确定P值。首先,你需要计算卡方统计量(χ²)和确定自由度(df)。
- 在卡方分布表中找到对应的自由度,然后找到大于或等于你的卡方统计量的值。
- 对应的表格值就是你的P值或者P值范围。
统计软件:
- 使用统计软件(如SPSS、R、Stata、Excel等)进行卡方检验,软件会直接给出P值。
- 在R语言中,可以使用
chisq.test()函数来进行卡方检验,它会返回包括P值在内的完整检验结果。- 在Excel中,可以使用
CHIDIST函数来计算给定卡方值和自由度的P值。在线计算器:
使用在线卡方检验P值计算器输入你的卡方统计量和自由度,计算器会给出P值
五、Python实现交叉列联分析和卡方检验
(一)导入库
from scipy.stats import chi2_contingency
import numpy as np(二)输入列联表数据
# 假设observed是观察频数列联表,例如此例题中的两个分类变量的频数分布
observed = np.array([[ 20, 30],[25, 25]])(三)使用chi2_contingency函数执行卡方检验
chi2, p, dof, expected = chi2_contingency(observed)(四)输出卡方统计量
print("Chi-square statistic:", chi2)
(五)输出P值
print("Expected frequencies:")
print(expected)print("P-value:", p)
(六) 输出自由度
print("Degrees of freedom:", dof)
(七) 输出理论频数
print("Expected frequencies:")
print(expected)
























线程池原理与实践 | 13.1、实现原理)



