1 引言
树高千丈,叶落求索 – 唐代杜牧
树结构在MySQL中常用于表示层次关系,如组织结构或分类体系。引入树结构可使数据之间建立父子关系,便于查询和管理。益处包括快速检索子节点、方便展示层次关系、支持递归查询等。
2 基础概念
2.1 名词解析
程序就像是一张有向图,你需要跟着边走才能找到正确的路径。
- 节点(Node):图中的基本元素,通常用来表示实体或对象。在计算机科学中,节点可以是任何数据结构中的元素,如树中的节点或图中的顶点。
- 边(Edge):节点之间的连接关系,用来表示节点之间的关联或连接。在图论中,边可以是有向的(箭头表示方向)或无向的(双向连接)。
- 路径(Paths):在图论中,路径是图中节点的序列,其中相邻节点通过边相连。路径可以是简单路径(不经过重复节点)或环路(起点和终点相同的路径)。
- 循环(Cycles):循环是图中形成闭合回路的路径,即起点和终点相同的路径。循环可以是简单循环(不经过重复节点,除起点和终点外)或包含重复节点的循环。
- 稀疏度(Sparsity):是指图中边的数量与可能存在的最大边数之间的比率。在稀疏图中,边的数量相对较少,而在稠密图中,边的数量相对较多。这个概念通常用于描述图的结构和连接性。
- 图遍历(Traversing graphs): 图遍历是一种算法,用于访问图中的所有节点或特定节点,以便对图进行分析或搜索。常见的图遍历算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。DFS沿着图的深度遍历节点,而BFS则逐层遍历节点。这些算法在解决许多图相关问题时非常有用,如寻找路径、检测环路、拓扑排序等。
- 树(Trees):树是一种层次性的数据结构,由节点(顶点)和边组成,其中每个节点最多有一个父节点,但可以有多个子节点。树的一个节点称为根节点,它没有父节点。树中除了根节点外,每个节点都有且仅有一个父节点。树的节点之间通过边连接,形成层次结构,从根节点到任意节点都有唯一的路径。树常用于表示层次关系,如组织结构、文件系统等。树的一些重要概念包括深度(节点到根节点的距离)、高度(树的最大深度)、叶节点(没有子节点的节点)等。树还有许多变种,如二叉树(每个节点最多有两个子节点)、二叉搜索树(左子节点小于父节点,右子节点大于父节点)等,它们在不同场景下有不同的应用和特性。
- 欧拉路径(Euler Paths):欧拉路径是指在图论中,经过图中每条边恰好一次的路径。如果一个图包含欧拉路径,则称该图具有欧拉路径性质。欧拉路径可以从一个节点出发,经过每条边一次且仅一次,最终回到另一个节点,或者以某个节点结束而不回到起点。欧拉路径在解决一些图相关问题时非常有用,如在网络中找到一条包含所有边的路径,或者在游戏中找到一条经过所有关键点的路径。欧拉路径的存在性和性质受到图的结构和边的连接方式的影响,因此对于不同类型的图,欧拉路径的判断和寻找方法也会有所不同。
2.2 图的模型设计
在计算机传统上,表达图的结构关系可以使用边缘列表、邻接表或邻接矩阵其中之一来体现。
边缘列表
- 概念:边缘列表是一种简单的图表示方法,其中每条边都列为一对顶点。
- 优点:
易于实现和理解。
对于边较少的稀疏图效率高。 - 缺点:
对于边较多的稠密图效率低。
查找与顶点相邻的所有边可能较慢。
邻接表
- 概念:邻接表是一种数据结构,用于表示图,其中每个顶点维护其相邻顶点的列表。
- 优点:
对于边较少的稀疏图效率高。
对于稀疏图,比邻接矩阵占用更少内存。 - 缺点:
对于某些操作,如检查两个顶点之间是否有边,速度较慢。
对于边较多的稠密图,需要更多内存。
邻接矩阵
- 概念:邻接矩阵是一个二维数组,其中两个顶点之间存在边的情况用1表示。
- 优点:
对于边较多的稠密图效率高。
允许快速查找边。 - 缺点:
对于边较少的稀疏图效率低。
对于稀疏图,比邻接表占用更多内存。
3 基础模型
3.1 图内容
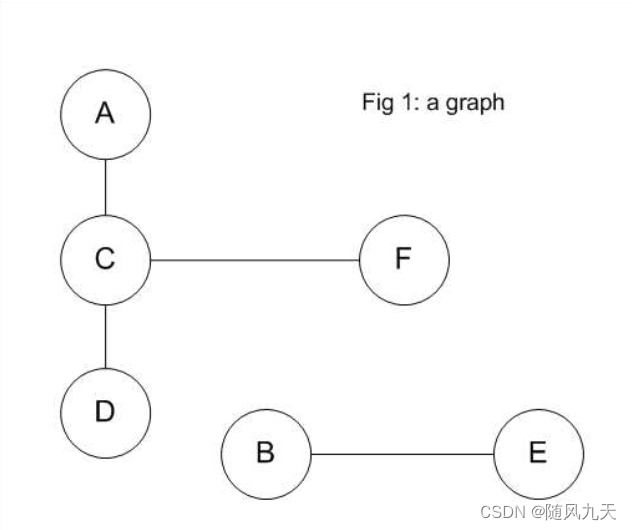
3.2 表结构和数据
创建表结构并且初始化数据:
CREATE TABLE nodes (
nodeID CHAR ( 1 ) PRIMARY KEY
);CREATE TABLE edges(childID CHAR(1) NOT NULL,parentID CHAR(1) NOT NULL,PRIMARY KEY(childID, parentID)
);INSERT INTO nodes VALUES ('A'), ('B'), ('C'), ('D'), ('E'), ('F');
INSERT INTO edges VALUES ('A','C'), ('C','D'), ('C','F'),('B','E');查询数据:
SELECT * FROM edges;
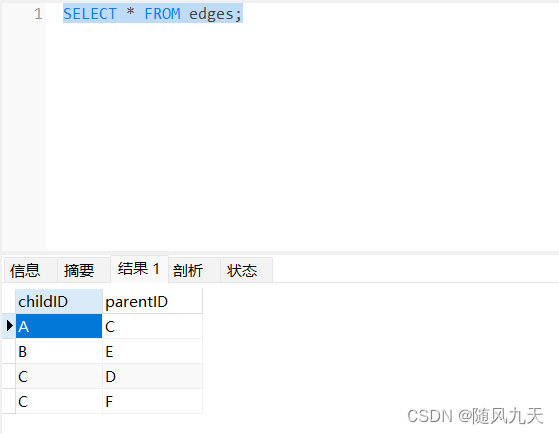
3.3 宽度优先搜索
3.3.1 编写存储过程
定义存储过程,如下:
DROP PROCEDURE IF EXISTS ListReached;
DELIMITER go
CREATE PROCEDURE ListReached (IN root CHAR(1))
BEGINDECLARE rows1 SMALLINT DEFAULT 0;DROP TABLE IF EXISTS reached;CREATE TABLE reached (nodeID CHAR(1) PRIMARY KEY) ENGINE= HEAP;INSERT INTO reached VALUES ( root );SET rows1 = ROW_COUNT();WHILE rows1 > 0 DOINSERT IGNORE INTO reached SELECT DISTINCT childID FROM edges AS e INNER JOIN reached AS p ON e.parentID = p.nodeID;SET rows1 = ROW_COUNT();INSERT IGNORE INTO reached SELECT DISTINCT parentID FROM edges AS e INNER JOIN reached AS p ON e.childID = p.nodeID; SET rows1 = rows1 + ROW_COUNT();END WHILE;SELECT * FROM reached;DROP TABLE reached; END;
go DELIMITER;
调用存储过程:
call ListReached( 'A');
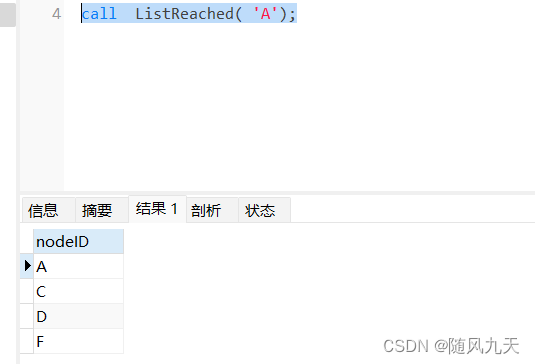
3.3.2 使用CTEs
从A 开始搜索:
WITH RECURSIVE cte AS (SELECTchildID,parentID,1 AS LEVELFROMedgesWHEREchildId = 'A' UNION ALLSELECTt.childID,t.parentID,c.LEVEL + 1FROMedges t


)
)



)


序列类图表)



-树状体系图)



