1.概念
- 有监督学习
- 正向传播:输入样本---输入层---各隐层---输出层
- 反向传播:误差以某种形式在通过隐层向输入层逐层反转,并将误差分摊给各层的所有单元,以用于修正各层的权值
- 激活函数:也叫阶跃函数,目的是引入非线性因素,有很多种激活函数,如sigmoid,relu,使用情景如下

- 激活函数作用:如果没有激活函数,则不管有几个隐藏层,都只能表示线性切割,即与单层神经网络相同,而通过使用激活函数,神经网络的每一层都可以学习输入数据的非线性变换,这使得整个网络能够逼近任何复杂的函数。解释如下图。

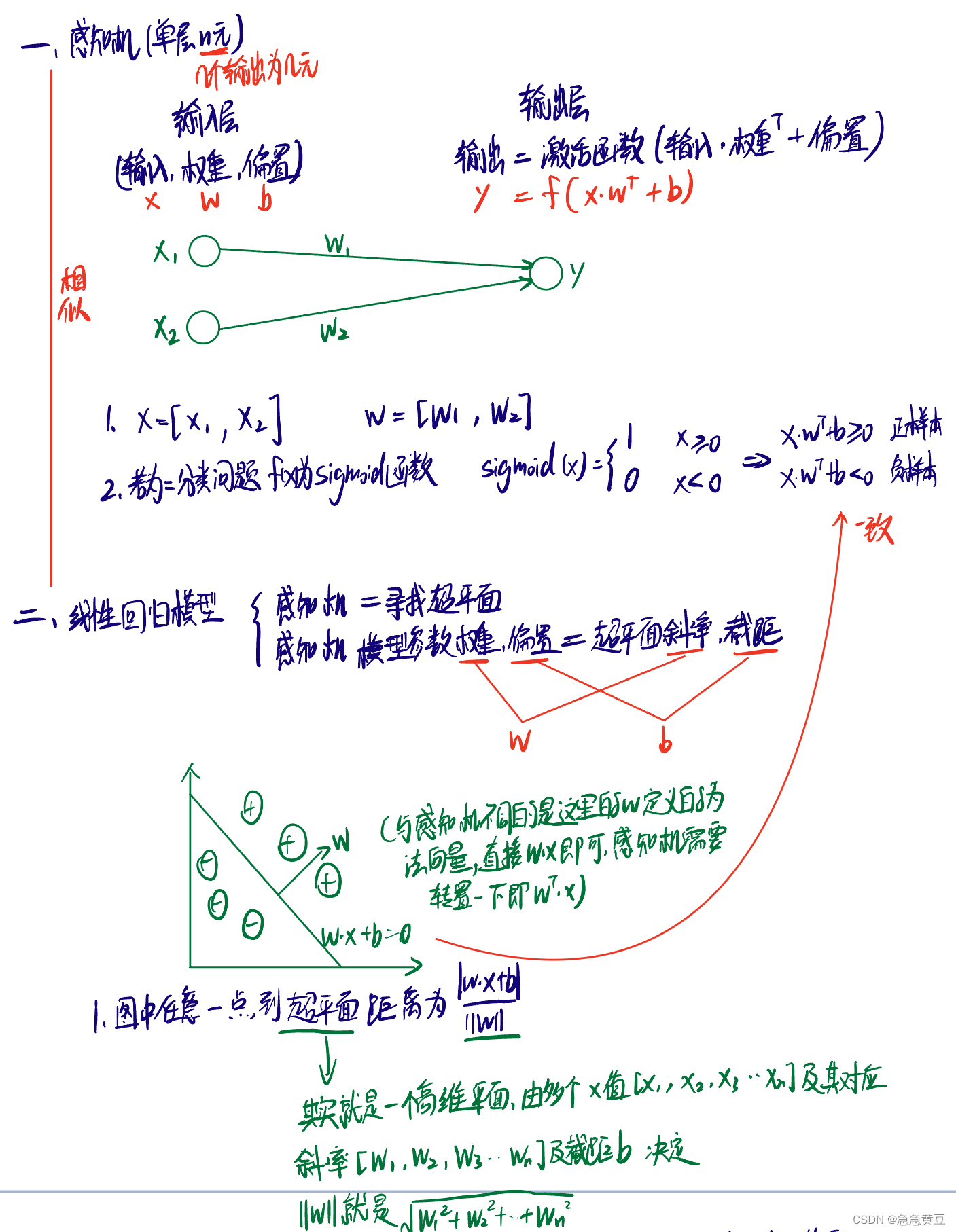
1.感知机(处理二分类问题)
1.1.概念及与线性回归模型的比较
1.2.梯度下降思想调整感知机参数w和b:
(1)损失函数为误分点到超平面距离的和
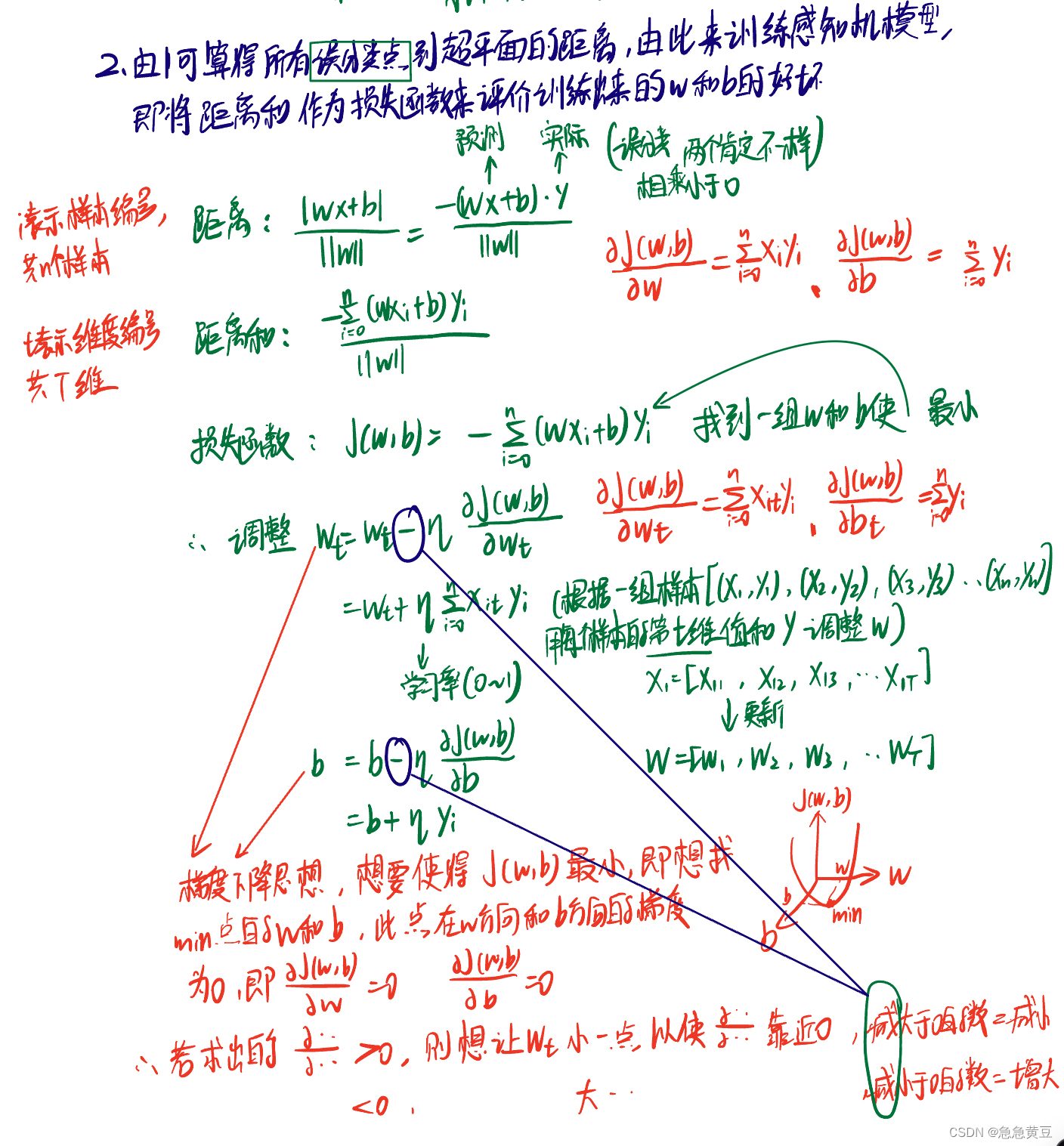
书上推理补充:

3.多层前馈神经网络
3.1.思想:
任意复杂连续函数都是n个一般线性函数的叠加,即感知机相当于一个线性函数,那增加n个隐层就可表示任意复杂连续函数。
3.2.区分
(1)感知机为单层网络
(2)加一个隐层为两层网络,也叫单隐层网络
3.3.误差逆传播算法BP算法
(1)用于多层前馈神经网络或其他类型网络,采用链式法则计算各层参数的梯度,然后使用梯度下降法来更新参数,以减小误差。
(2)损失函数为每个预测y值与样本实际y值之差绝对值的和

3.4.标准BP算法与累计BP算法
类似随机梯度下降(每次迭代中仅使用一个样本来计算梯度)、标准梯度下降(整个数据集来计算梯度)
- 标准BP算法:更新频繁;需要更多次数迭代
- 累计BP算法:读取整个训练集后才更新,频率低;更快获得较好解(数据集大更明显)

3.5.过拟合解决方案
过拟合表现:训练误差持续降低,测试误差可能上升
(1)早停:
- 若训练误差降低但测试误差上升,则停止
- 返回最小测试误差的权重和偏置(阈值)
(2)正则化:
- 增加描述网络复杂度的部分,eg权重和阈值的平方和,想要这部分也小一点,别太复杂
- 损失函数变为了\lambda*经验误差+(1-\lambda)*网络复杂度,其中经验误差就是我们上面一直用的损失函数,即预测y与实际y值的差和
4.全局最小与局部极小
在神经网络中,我们对样本进行训练,对于训练得到的结果,我们通过损失函数计算调整权重和阈值,在这个过程中,不管是感知机还是多层前馈网络使用的都是梯度下降策略,希望找到损失函数在某个参数(权重或阈值)方向上的是极小值的点,也就是寻找损失函数在某参数上偏导为0的点,若不为0,则调整该参数使得在损失函数上的取值向最低点靠近。在这个过程中,涉及到一个全局最小和一个局部极小的概念,即如果有多个极小点,那么根据梯度下降很可能找到的是一个局部最小点,而不是全局最小点。解决方案如下:
- 多组不同参数值的神经网络出发
- 模拟退火算法,每一步有一定概率接受比当前更差的结果
- 随机梯度下降,在梯度为0时计算出来的梯度仍可能不为0
5.其他神经网络
(1)PBF网络:单隐层、径向基函数作为隐层神经元激活函数
(2)ART 网络:无监督学习策略、输出神经元相互竞争,每一时刻仅有一个神经元被激活、可塑性-稳定性
(3)SOM 网络:竞争型、无监督神经网络、将高维数据映射到低维空间(通常为2维)同时保持输入数据在高维空间的拓扑结构
(4)级联相关网络
(5)Elman 网络:不同于前馈神经网络,elman是一种递归神经网络,神经元的输出反馈回来作为输入信号
(6)Boltzmann 机:基于能量的模型
6.深度学习模型
模型深度和宽度都较大,其中增加隐层的数目比增加隐层神经元的数目更有效,由于复杂则难以直接用经典算法(例如标准BP算法)进行训练。
训练方法:
(1)无监督逐层训练:预训练(训练时将上一层隐层结点的输出作为输入)+微调(一般使用BP算法),可以先找到局部看起来比较好的设置, 然后再基于这些局部较优的结果联合起来进行全局寻优
(2)权共享:一组神经元使用相同的连接权值,卷积神经网络就是这样
**卷积神经网络:
(1)卷基层:含n个特征映射,每个特征映射为由多个神经元构成的“平面”
(2)采样层:汇合层,减少数据量的同时保留有用信息
(3)连接层:每个神经元被全连接到上一层每个神经元, 本质就是传统的神经网络
激活函数采用修正线性函数relu;可用bp算法训练;每一层的权值都相同,好训练


)



2)
: 了解和使用state)





)





