5月31号，明天决赛，今天脑子也是一滩浆糊，踏马的一道题也做不出来，超级难受，只好简单复盘一下两道之前的题目，看完就差不多了，再学也没啥用了，写完这两题题解我就回去打把steam绝地求生，听天由命等死吧

复盘之前基础题：

一、经典动态规划：最长递增子序列

很基础的动态规划题，思路如下：

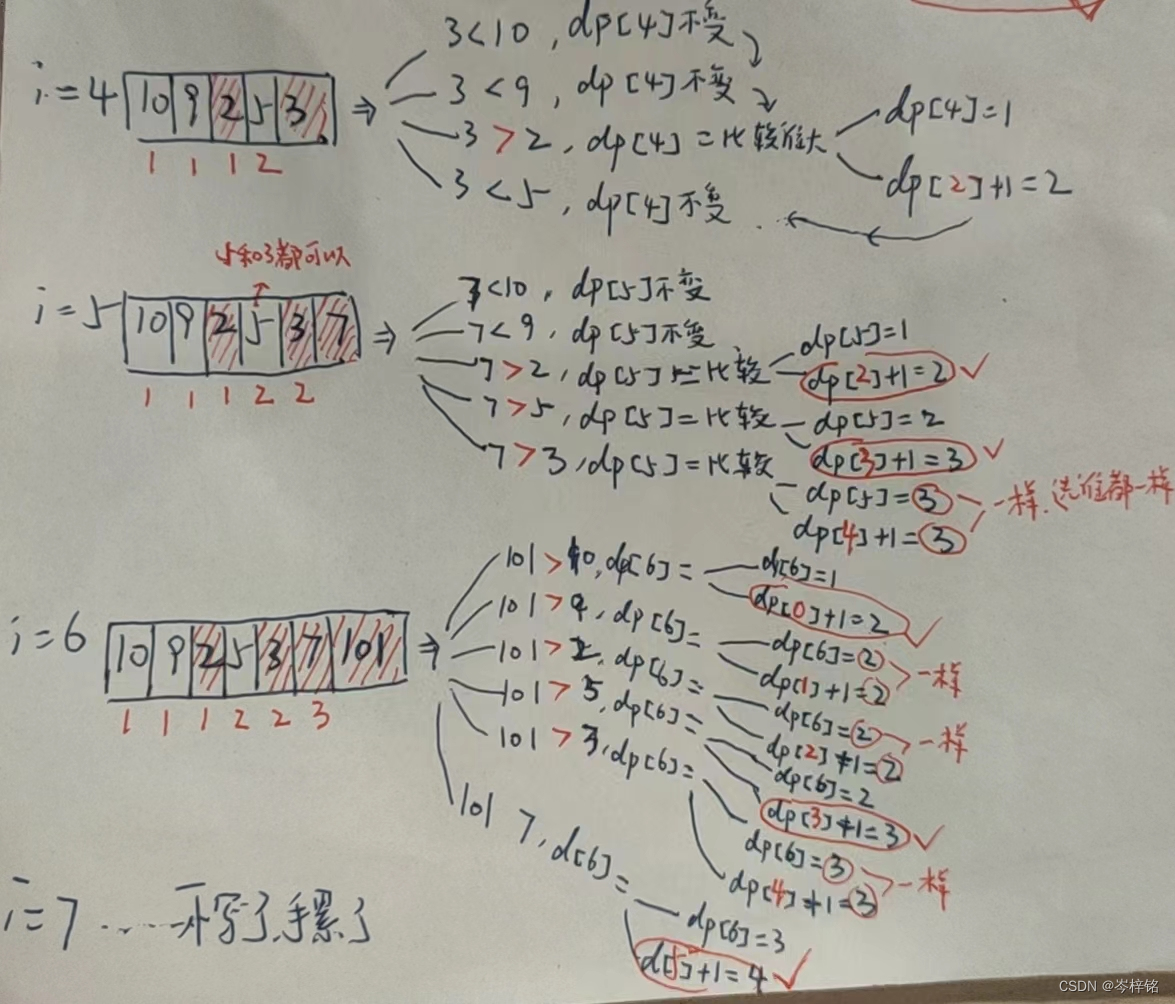
我们遍历整个数组，每遍历到第 i 位，我们就把【从第0位 ~ 第i位】作为一个新数组，来计算以这个第 i 位为结尾的数组里，可以跟第 i 位组成最长递增子序列的长度是多少

我们用一个dp[ ]数组记录下每一个以第 i 位结尾的最长递增子序列的长度是多长

那么我们知道，假如 j < i，如果 “第 j 位的数 < 第 i 位的数” ，那么第 i 位的数就可以跟【以第 j 位为结尾的最长递增子序列】组成一个新的最长子序列

那这个【以第 i 位为结尾的最长递增子序列】的长度就等于 ——>【以第 j 位为结尾的最长递增子序列】的长度+1

完整代码：

import java.util.Arrays;
import java.util.Scanner;public class 最长递增子序列 {public static void main(String[] args){//我这里懒得按照题目要求输入了，直接输入原数组序列，知道逻辑就行Scanner in = new Scanner(System.in);System.out.print("请输入这个数组有几个成员：");int n = in.nextInt();System.out.print("请输入这"+n+"个数字：");long []a = new long[n];for (int i = 0; i < n; i++) {a[i] = in.nextLong();}long[] dp = new long[n];Arrays.fill(dp,1);//全部初始化为1，也就是每个第i位数字自己就是一个数组的时候的长度就是1long maxLength = 1;//记录最大递增子序列的for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if(a[j] < a[i]){dp[i] = Math.max(dp[i] , dp[j]+1);}}maxLength = Math.max(maxLength , dp[i]);}System.out.println(maxLength);}
}

二、经典动态规划：最长递增子序列的个数

在上一题的基础要统计个数，看似烧脑麻烦，但其实多写几组样例还是能看出简单的规律的

思路：

1、我们除了用dp[ ]数组记录每一个的最长子序列的长度以外，再设一个count[ ]数组，记录每一个【以第 i 位为结尾的数组】有几个最长递增子序列

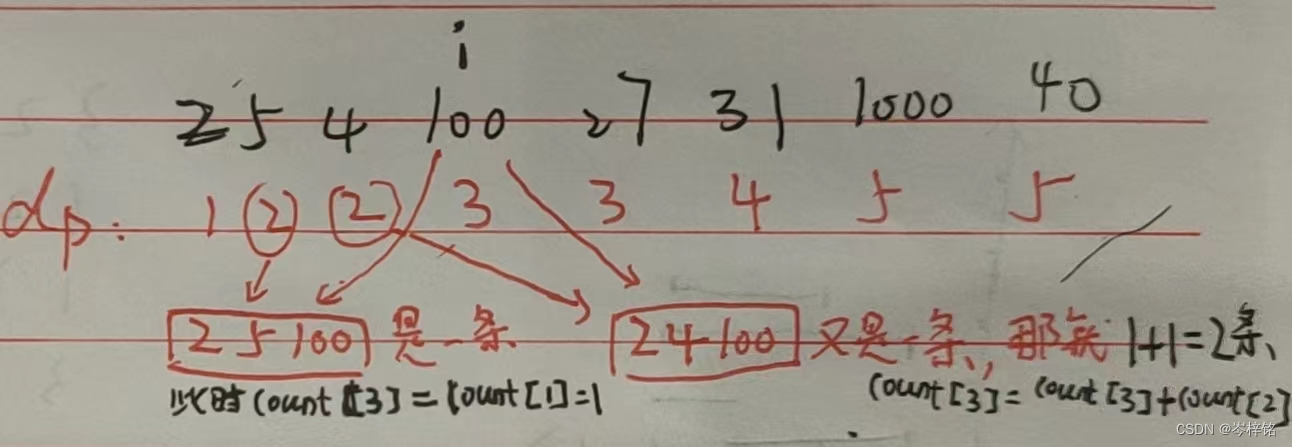
2、如果dp[ j ] + 1 > dp[ i ]，那么就说明【以第 j 位为结尾的最长递增子序列】可以跟【第 i 位】组成新的最长子序列，那么第 j 位有几个最长递增子序列，第 i 位也就跟他一样有几个

即：count[i] = count[j]

（趣味理解：j 有N个最长递增子序列，那我 i 是他爹，我更应该也有N个）

3、如果dp[ j ] + 1 == dp[ i ]，那么就说明找到了相同长度的递增子序列，那么就应该在count[ i ]原来最多有N条的最长子序列的基础上，再加上count[ j ]拥有的最多的递增子序列

即：count[i] += count[j]

（趣味理解：j 跟 j+1 都有10万块，那我CEO在本来就有15万的基础上，也要再加10万块）

4、不过还是要建立在a[ j ] < a[ i ]的情况，你都不比他大就说明你们凑不成一个递增子序列

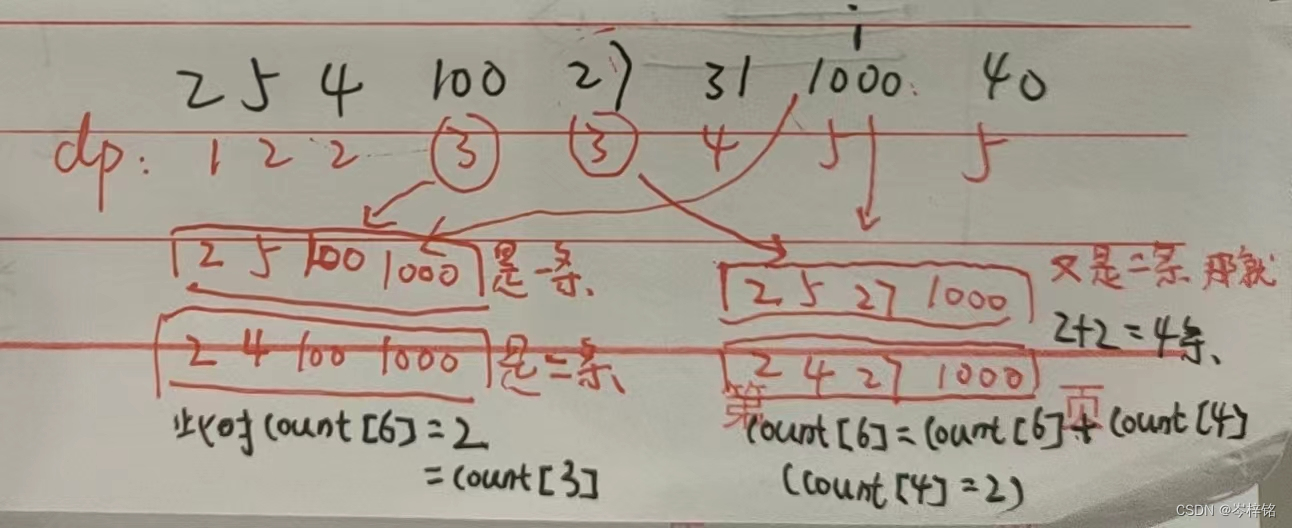
5、但是因为我们根据dp[ j ] + 1 > dp[ i ] 和 dp[ j ] + 1 == dp[ i ]来更新最多的递增子序列的个数，那么我们只能获取到“【以i为结尾的】、【最后长度最长】”的递增子序列的个数，但是要知道最后结尾的数也可能不止一个

按照这个例子，那么我们实际想要的是【以7为结尾的最长子序列】2个 + 【以6为结尾的最长子序列】2个 = 4个！！

那么就还得用一个【maxLength】记录下最长子序列的长度

然后遍历dp[ ]数组，找到最后长度是最长子序列长度的位置if (dp[ i ] == maxLength)

然后把这些位置为结尾的拥有的最长子序列的个数累加resulet += count[ i ]

最后这个result才是整个原数组拥有的最长递增子序列的个数

（趣味理解：最后两个同级别的CEO大佬，都掌握2亿资产，那么它两加起来的4亿才是这个公司最屌工资的总数）

完整代码：

import java.util.*;
public class 最长递增子序列的个数 {public static void main(String[] args){//我这里懒得按照题目要求输入了，直接输入原数组序列，知道逻辑就行Scanner in = new Scanner(System.in);System.out.print("请输入这个数组有几个成员：");int n = in.nextInt();System.out.print("请输入这"+n+"个数字：");long []a = new long[n];for (int i = 0; i < n; i++) {a[i] = in.nextLong();}long[] dp = new long[n];long[] count = new long[n];Arrays.fill(dp,1);Arrays.fill(count,1);long maxLength = 0;//记录最大递增子序列的for (int i = 0; i < n; i++) {for (int j = 0; j < i; j++) {if(a[j] < a[i]){if(dp[j]+1 > dp[i]){dp[i] = dp[j]+1;count[i] = count[j];} else if (dp[j]+1 == dp[i]) {count[i] += count[j];}}}maxLength = Math.max(maxLength , dp[i]);}long result = 0;for (int i = 0; i < n; i++) {if(dp[i] == maxLength){result += count[i];}}System.out.println(result);}
}

不写了玛德，心烦了，只想吃个鸭腿跟热卤，回去打两把游戏睡觉