题目大意就是t组数据,每组一个左右边界l,r,问区间内的两个是xi,yi是区间内max(gcd(xi,yi)),数据范围是1e12.

答案就是找到第一个a*x<b*x(a<b),他们两在l到r之间且x最大,那么x就是答案,可以知道,要使两个数在区间内,那么他们之间的差值要小于min(R-L,[R/2]),[]表示向下取整

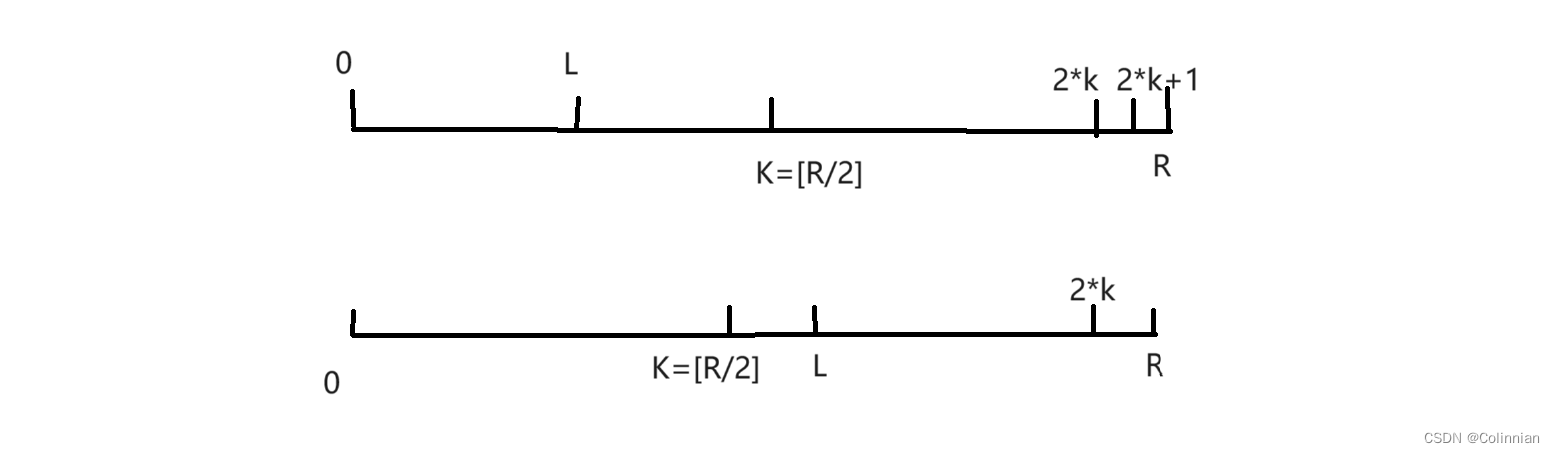
看着两种情况,第一种情况,2*k是最后一个能被2整除的数,所以如果2*k不等于R的话那么在2*k右边不可能出现大于等于2*k+2的数,及只有2*k+1,且R不等于2*k,所以R=2*k+1,第二种情况及2*k==R,如果r/2在[l,r]之间,那么k必然是我们要找的最大的gcd,因为根据上面的推断,这个时候a=1,b=2,显然此时x最大.如果k小于l,那么答案必定是小于r-l的这很好判断吧.

那么现在为了让a和b最小,我们来看M,2M,3M,3M表示在L,R区间内最后一个能整除3的,这个时候就有好几种情况了,先分析1.如果3M>2K,那么3M右边必定没有数字,因为在之前分析了,2K右边最多有一个数字,所以这个的3M显然等于R,第二种情况就是3M<2K,如果2K等于R,那么右边没有数字,这种情况下只有K在L左边才会发生,即R-L<K的时候才会发生,否则在2*k的时候就是已经找到答案了,就不会进行到分析3的情况了,为什么不先选择3而去选择2,因为当我们计算最后一个能整除K的数字的时候,使用[R/K]*K,那么对于K*n,和在区间内或者不在区间内的n*k,n*(k-1)....一直到n,他们的最大公约数必然是n,即[R/K],显然[R/K]随着K的增大而减小,所以要找最大的x,就按顺序增大k就好.接下来回到3,刚才我们说到3*m右边有一个数,一种是2*k在3*m右边,这时说明2*k不满足,直接看3*m是否满足即可,第二种是右边不是2*k,这种情况不存在,如果2*k在3*m左边,那就不满足2*k右边至多有一个数的条件了.下一种情况是3*m右边没有数字,那么就不需要证明什么,2*m在范围内,那么答案就是m,第三是3*m右边有两个数,显然2*k=3*m+1,那么由于2*k是最后一个能被2整除,3*m是最后一个能被3整除的数,3*m+2显然最小能被4整除,写个不等式(3*m+2)/4显然小于等于m,在m都是正整数的时候.当然其它情况以此类推.

我们最终能得出的结论是:[L,R]范围内的max(gcd(x,y))是一个[R/k]*(k-1)且在范围内的[R/k],

using ll = long long;
void solve() {ll l, r;std::cin >> l >> r;ll x = std::min(r - l, r / 2);for (; x >= 1; x = r / (r / x + 1)) {if (r - r % x - x >= l) {std::cout << x << '\n';break;}}
}
int main() {int t;std::cin >> t;while (t--) {solve();}return 0;
}

代码解释,x初始化为最大区间,r/x表示能容纳该区间的区间数,+1表示区间数+1,然后再用r/(r/x+1)及表示当相同区间数+1后区间的大小,r-r%x计算的是左边界,去掉r%x以后前面是一个均分的每个区间大小为x的区间,再减去一个x,因为我们要在[l,r]内容纳两个区间,如果它大于等于左边界,就说明找到答案了.