最终一致性分布式事务概述
强一致性分布式事务解决方案要求参与事务的各个节点的数据时刻保持一致,查询任意节点的数据都能得到最新的数据结果,这就导致在分布式场景,尤其是高并发场景下,系统的性能受到了影响。而最终一致性分布式事务解决方案并不要求参与事务的各个节点数据时刻保持一致,运行其存在中间状态,只要一段时间后,能够达到数据的最终一致状态即可,在电商场景中使用比较多
典型方案
业界基于Base理论提出的最终一致性分布式事务解决方案有:
- TCC解决方案
- 可靠消息最终一致性解决方案
- 最大努力通知型解决方案
优缺点
最终一致性分布式事务解决方案的优点:
- 性能比较高,这是因为最终一致性分布式事务解决方案不要求数据时刻保持一致,不会因为长时间持有事务占用的资源而过度消耗过多的性能
- 具备可用性
- 适合高并发场景
最终一致性分布式事务解决方案的缺点:
- 因为数据存在短暂的不一致,所以在某个时刻查询出的数据状态可能会不一致
- 对于事务一致性要求特别高的场景不适用
服务模式
- 可查询操作:需要服务操作具有可标识性,主要体现在服务的操作具有全局唯一的标识,可以是业务的单据编码(如订单号)也可以是系统分配的操作流水号,另外在可查询的服务模式中,也要有完整的操作时间信息
- 幂等性操作:指对同一个方法,只要参数相同,无论执行多少次都与第一次执行时产生的影响相同,为了保证数据的最终一致性,系统会提供很多次重试操作,这个时候就需要接口实现幂等性操作
- TCC操作:这个模式下包括了3个阶段,Try阶段(尝试业务执行)、Confirm阶段(确认业务阶段)和cancel阶段(取消业务执行)
Try阶段
- 完成所有业务的一致性检查
- 预留必要的业务资源,并需要与其他操作隔离
Confirm阶段
- 此阶段会真正执行业务操作
- 因为在Try阶段完成了业务的一致性检查,所有此阶段不会做任务业务检查
- 只用Try阶段预留的业务资源进行操作
- 此阶段的操作需要满足幂等性
Cancel阶段
- 释放Try阶段预留的业务资源
- 此阶段的操作需要满足幂等性
- 可补偿操作:某些数据处于不正常的状态,需要通过某种方式进行业务补偿,使数据能够达到最终一致性,这种因数据不正常而进行的补偿操作,就是可补偿操作服务模式
TCC解决方案
TCC是一种典型的解决分布式事务问题的方案,主要解决跨服务调用场景下得分布式事务问题,广泛应用于分布式事务场景
适用场景
用于具有强隔离性,严格一致性要的业务场景,也适用于执行时间比较短的业务,对于电商场景中下得减库存等业务,如果使用TCC分布式事务,则会经历Try、Confirm、Cancel三个阶段
需要实现的服务模式
在TCC分布式事务解决方案中,需要实现的服务模式包括TCC操作,幂等操作、可补偿操作、可查询操作。
例如实现TCC分布式事务方案时,需要实现Try、Confirm、Cancel三个阶段的业务逻辑,这就是TCC操作,在TCC操作的每个阶段的方法都需要实现幂等性,这就是幂等操作,如果在执行分布式事务过程中业务服务出现了异常情况,则需要支持重试阶段,以达到事务补偿的目的,这就是可补偿操作,另外业务服务需要提供可以查询自身内部事务状态的接口,以供其他服务调用,这就是可查询操作
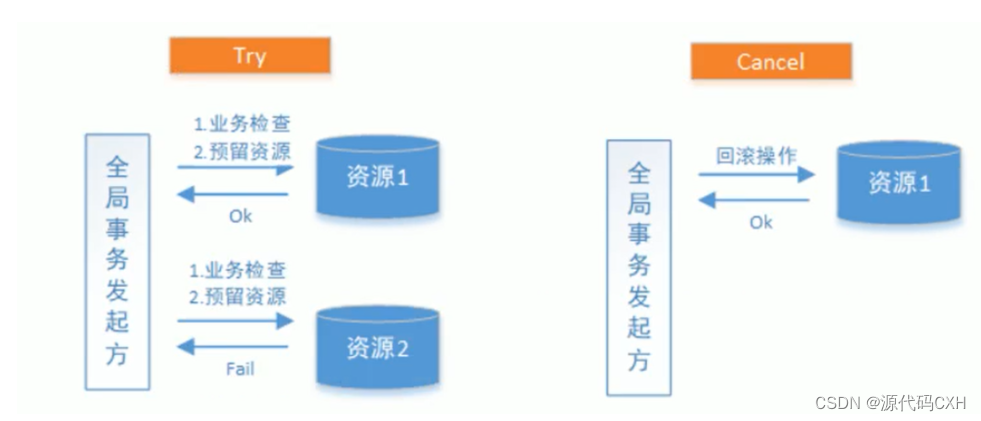
分支事务失败的情况:
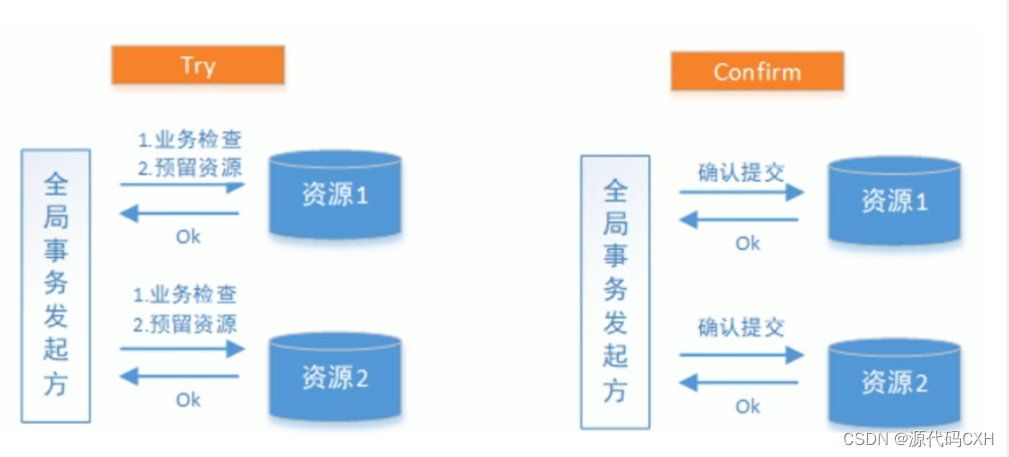
本质上讲,TCC是一种应用层实现的二阶段提交协议,TCC方案的执行流程如下
- Try阶段:不会执行任务业务逻辑,仅做业务的一致性检查和预留相应的资源,这些资源能够和其他操作保持隔离
- confirm阶段:当Try阶段所有分支事务执行成后开始执行Confirm阶段,通常情况下,采用TCC解决分布式事务时会任务Confirm阶段是不会出错的,也就是说,只要Try阶段的操作执行成功了,Confirm阶段就一定会执行成功,如果Confirm阶段出错了,就需要引入重试机制或者人工处理,对出错的事务进行干预
- Cancel阶段:在业务执行异常或出现错误的情况下,需要回滚事务的操作,执行分支事务的取消操作,并且释放Try阶段预留的资源,通常情况下,采用TCC方法解决分布式事务时,同样会认为Cacnel阶段也是一定会执行成功的,如果出现错误,就需要引入重试机制或者人工处理,对出错的事务进行干预
方案的优缺点
TCC方案的优点
- 在应用层实现具体的逻辑,锁定资源的粒度变小,不会锁定所有资源,提升了系统的性能
- Confirm阶段和Cancel阶段的方法具备幂等性,能够保证分布式事务执行完毕后数据的一致性
- TCC分布式解决方案有主业务发起整个事务,无论主业务还是分支事务所在的业务,都能部署为集群模式,从而解决了XA规范的单点故障问题
TCC方案的缺点
- 代码需要耦合到业务中,每个参与分布式事务的业务方法都要拆成Try、Confirm、Cancel三个阶段的方法,提高了开发的成本
需要注意的问题
使用TCC方案解决分布式事务问题时,需要注意空回滚、幂等和悬挂问题
空回滚问题
- 原因:出现空回滚的原因是一个分支事务所在的服务器宕机或者网络发生异常,此分支事务调用失败,此时并未执行此分支的Try阶段的方法,当服务器或者网络恢复后,TCC分布式事务执行回滚操作,会调用分支事务的Cancel阶段的方法,如果Cancel阶段的方法不能处理这种情况,就会出现空回滚的问题
- 解决方案:识别是否出现空回滚操作的方法是判断是否执行了Try阶段的方法,如果执行了Try阶段的方法,就没有空回滚,否则则出现空回滚
幂等问题
- 原因:由于服务器宕机、应用崩溃或者网络异常等原因,可能会出现方法调用超时的情况,为了保证方法的正常执行,往往会在TCC方案中加入超时重试机制,因为超时重试有可能导致数据的不一致问题,所以需要保证分支事务的执行以及TCC方案的Confirm阶段和Cancel阶段具备幂等性
- 解决方案:在分支事务记录表中增加事务的执行状态,每次执行分支事务以及Confirm阶段和Cancel阶段的方法时,都查询次事务的执行状态,以此判断事务的幂等性
悬挂问题
- 原因:TCC分布式事务中,通过RPC调用分支事务Try阶段的方法时,会先注册分支事务,在执行RPC调用。如果此时发生服务器宕机,应用崩溃或者网络异常等情况,RPC调用就会超时,如果RPC调用超时,事务管理器会通知对于的资源管理器回滚事务,可能资源管理器回滚完事务后,RPC请求达到了参与分支事务所在的业务方法,因为此时事务以及回滚,所以在Try阶段预留的资源就无法释放了,这种情况下,就成为悬挂
- 解决方案:如果执行了Confirm阶段或者Cancel阶段的方法,则Try阶段的方法就不能再执行了,具体方案是在执行Try阶段的方法时,判断分支记录表中是否存在同一全局事务下Confirm阶段或者Cancel阶段的事务记录,如果存在,则不执行Try阶段的方法

散度)
)


)


:deepstream-app-示例演示)


![[[nodiscard]]--c++17](http://pic.xiahunao.cn/[[nodiscard]]--c++17)







