本文旨在基于机器学习方法,对一线城市租房价格进行预测分析,并使用Matplotlib可视化、随机森林、一元线性回归和多元线性模型进行模型对比。通过爬取北京链家二手房数据作为研究对象,探讨了租房价格与各种因素之间的关系,阐述了研究目的,即预测一线城市租房价格,以满足人们对于租房市场的需求。其次,介绍了理论与实际意义,指出准确预测租房价格对于租房者、房东和政府都具有重要意义,可以提供决策支持和参考依据。
本文主要研究内容包括数据采集、数据处理、特征选择和建立预测模型四个方面。使用request爬虫技术,从北京链家网站上获取了二手房数据,并进行了数据清洗和整理,以保证数据质量。通过特征选择方法,确定了与租房价格相关的特征变量。最后,采用了随机森林、一元线性回归和多元线性模型等机器学习算法,建立了预测模型,并对不同模型进行了比较和评估。
通过实验结果的分析,得出以下结论:随机森林模型在预测一线城市租房价格方面表现最好,具有较高的准确性和预测能力;多元线性模型次之;而一元线性回归模型的预测效果较差。同时,还对模型的优化和应用进行了讨论,并提出了进一步研究的方向和意见,为租房市场的决策制定提供了参考依据,具有一定的理论与实际意义。
一、课题来源、背景及其意义
1.1课题来源
本研究课题的来源是对当前一线城市租房市场需求的迫切性以及人们对租房价格走势的关注。随着城市化进程的加速和人口流动的增加,一线城市的房地产市场一直备受关注。租房作为一线城市居民的重要选择,其价格预测对于租房者、房东和政府都具有重要意义。
对于租房者来说,准确预测租房价格可以提供参考依据,帮助他们做出合理的租房决策。对于房东来说,可以提供租金定价的依据,提高租房效益。对于政府来说,可以为房地产政策制定和市场监管提供科学依据,促进租房市场的健康发展。
然而,目前存在着特征选择不够准确、模型预测精度有限等问题。因此,本研究旨在通过机器学习方法对一线城市租房价格进行预测分析,并使用matplotlib可视化技术呈现结果。同时,将与随机森林、一元线性回归和多元线性模型等传统模型进行对比,以提升租房价格预测的准确性和可靠性。
通过研究一线城市租房价格的预测,可以为租房市场参与者提供决策支持和参考依据,有助于优化租房资源配置,提高市场透明度。此外,本研究还将填补现有研究的空白,为相关领域的学术研究和实践提供新的思路和方法。
1.2研究目的及意义
1.2.1理论意义
基于机器学习的预测模型:通过应用机器学习算法,如随机森林、一元线性回归和多元线性模型等,对一线城市租房价格进行预测分析,可以在理论上推进租房价格预测方法的研究。这些模型能够从大量数据中自动学习并发现潜在的模式和关联性,提高预测准确性和可靠性。
matplotlib可视化技术:使用matplotlib可视化库,可以将预测结果以图表的形式直观地展示出来,增强了模型结果的可解释性。可视化技术可以帮助我们更好地理解数据之间的关系和趋势,为决策制定提供科学依据。
1.2.2实际意义
租房者决策支持:准确预测一线城市租房价格,能够为租房者提供决策支持和参考依据。他们可以根据预测结果来选择适合自己需求和经济能力的租房方式,节省时间和精力。
房东租金定价:对于房东来说,准确预测租房价格有助于他们合理定价,提高租房效益。通过比较不同模型的预测结果,房东可以制定更加科学合理的租金策略,降低空置率。
政府政策制定:准确预测一线城市租房价格对于政府制定房地产政策和市场监管具有重要意义。政府可以根据预测结果来制定合适的房地产政策,促进租房市场的健康发展,并为市场监管提供科学依据。
学术研究与实践应用:本研究填补了现有研究的空白,为相关领域的学术研究提供了新的思路和方法。同时,该研究还具有重要的实践应用意义,为房地产从业者和市场参与者提供了决策参考价值,促进了租房市场的健康发展。
三、主要研究内容
主要研究内容可以包括以下几个方面:使用Python爬虫技术从某房屋租售网站中爬取一线城市(北京)的租房数据。原始数据包含租金、面积、户型、朝向、区域、租房类型、地铁等变量。对数据进行清洗、去重和转换,处理缺失值和异常值,确保数据质量。同时进行租房价格影响因素的分析。通过探索性数据分析(EDA)和统计分析,探讨不同变量与租房价格之间的关系,如面积、户型、朝向、区域等。还可以分析其他因素,如租房类型、地铁站等是否对租房价格有显著影响。另外在数据集上进行特征选择,识别出对租房价格具有重要影响的特征变量。使用相关性分析、特征重要性评估等方法来选择最具预测能力的特征。然后,构建机器学习模型,如线性回归、决策树、随机森林等,来建立影响租房价格的模型。
对构建的影响租房价格的模型进行评估和解释。使用评估指标(如均方误差、决定系数)来评估模型的预测能力和稳定性。同时,对模型中的变量系数进行解释,了解各个因素对租房价格的贡献程度和方向。
3.1数据清洗与预处理
数据清洗与预处理的主要研究内容包括数据导入与列名设置、缺失值处理、重复值删除、变量转换和可视化分析等步骤。通过这些操作,可以为后续的影响因素分析和建模提供高质量的数据基础。
3.2租房价格影响因素的分析
租房价格影响因素的分析是研究中的核心内容,通过探索性数据分析和统计分析来确定可能影响租房价格的主要因素。以下是主要研究内容:
3.2.1变量关系探索
利用可视化工具绘制了房租价格直方图、房面积分布图和房面积与价格关系的散点图。这些图表有助于观察房租价格和其他变量之间的分布情况和趋势,并初步判断它们之间的关系。
3.2.2相关系数矩阵分析
计算了特征变量之间的相关系数矩阵,并使用热图进行可视化展示。通过观察相关系数,可以确定变量之间的线性相关性。这有助于识别出与房租价格强相关的特征变量,进一步深入分析其影响程度。
3.2.3楼层对房租价格的影响分析
通过绘制楼层分析的计数图,观察不同楼层的房屋数量分布。此外,还可以通过统计分析等方法,进一步研究楼层对房租价格的影响,例如分析不同楼层的平均价格和价格波动情况。
3.2.4特征箱线图分析
绘制了特征变量的箱线图,用于观察数据的分布情况和离群值。通过箱线图,可以发现异常值和不同特征变量之间的差异性,进而判断它们对房租价格的影响程度。
3.3特征选择与建模
特征选择与建模是研究中的关键步骤,旨在识别对租房价格具有显著影响的特征变量,并构建合适的机器学习模型进行预测。以下是主要的研究内容:
特征选择方法:通过计算特征之间的相关系数矩阵,使用热图可视化展示各个特征变量之间的相关性。利用相关系数矩阵和颜色编码,可以初步筛选出与租房价格强相关的特征变量。
单变量线性回归分析:使用一元线性回归模型,分析面积与价格之间的关系。通过拟合回归模型,计算回归系数和截距,进一步了解面积对租房价格的影响程度。同时,评估模型性能,如计算均方误差(MSE)和决定系数(R^2),以评估模型的预测能力。
多元线性回归分析:使用多元线性回归模型,考虑多个特征变量对价格的综合影响。通过构建回归模型,计算各个特征变量的回归系数和截距,进一步了解各个特征变量对租房价格的贡献程度。同样,评估模型性能,如计算均方误差(MSE)和决定系数(R^2)。
随机森林回归分析:使用随机森林回归模型进行特征选择和建模。通过网格搜索方法,寻找最优的超参数组合,并构建随机森林回归模型。通过计算均方误差(MSE)和决定系数(R^2),评估模型的预测性能。
3.4模型评估与解释
模型评估与解释是研究中的重要环节,旨在对构建的影响租房价格的模型进行评估和解释。以下是主要的研究内容:
线性回归模型评估与解释:通过计算一元线性回归模型和多元线性回归模型的均方误差(MSE)和决定系数(R^2),来评估模型的预测能力和稳定性。较低的均方误差和较高的决定系数表示模型拟合良好。此外,还可以解释回归模型的系数和截距,了解各个特征变量对租房价格的贡献程度和方向。
随机森林回归模型评估与解释:通过网格搜索方法,寻找最优的超参数组合,并构建随机森林回归模型。使用测试集数据,计算预测结果与真实值之间的均方误差(MSE)和决定系数(R^2),评估模型的预测性能。此外,还可以解释随机森林回归模型中各个特征变量的重要性,了解它们对租房价格的贡献程度。
模型解释与可视化:对构建的模型进行解释,包括线性回归模型和随机森林回归模型。可以通过查看模型的系数、截距以及特征重要性等指标,了解各个特征变量对租房价格的影响程度和方向。此外,还可以使用可视化工具绘制模型预测结果与真实值之间的散点图或折线图,以便更直观地理解模型的拟合情况。
数据可视化分析
绘制直方图:使用matplotlib.pyplot的hist()函数绘制价格的直方图。
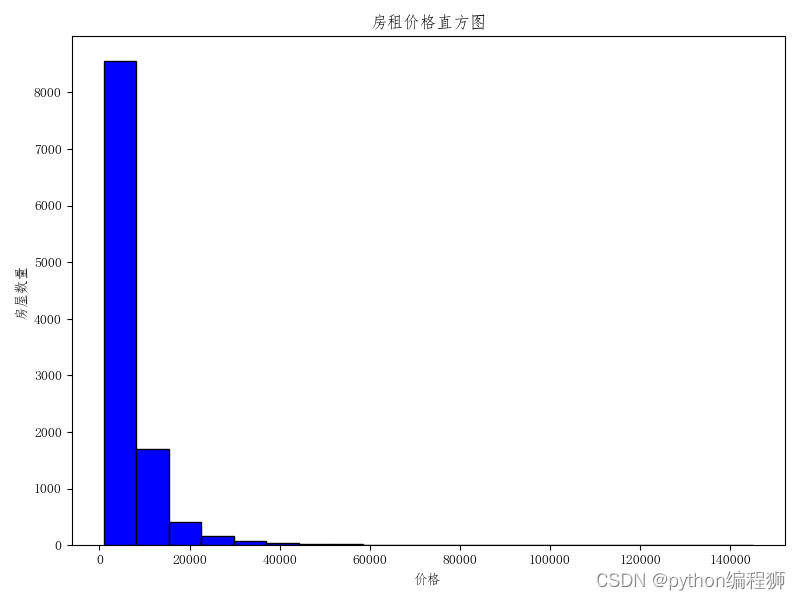
图4
由图四可知,北京租房价格分布大多数集中在0-20000元,超过60000元的租房数量几乎为0.
面积特征分析
面积特征分析,是基于租房面积,对租房进行统计分析。将租房面积划分不同的区间,同时,结合租房价格,验证租房面积越大,价格是否越昂贵。
绘制房面积分布情况和价格关系:使用seaborn库的distplot()函数绘制房面积的分布情况和regplot()函数绘制房面积与价格的关系图。
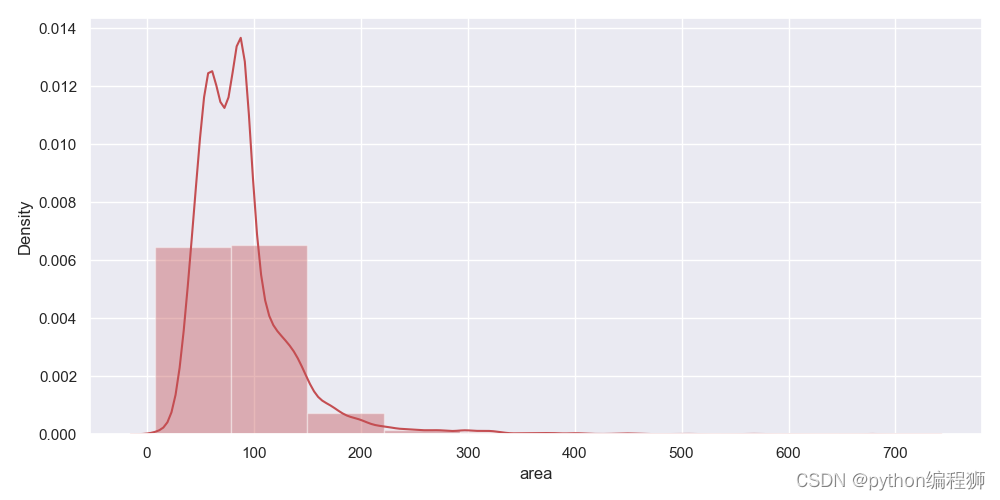
图5
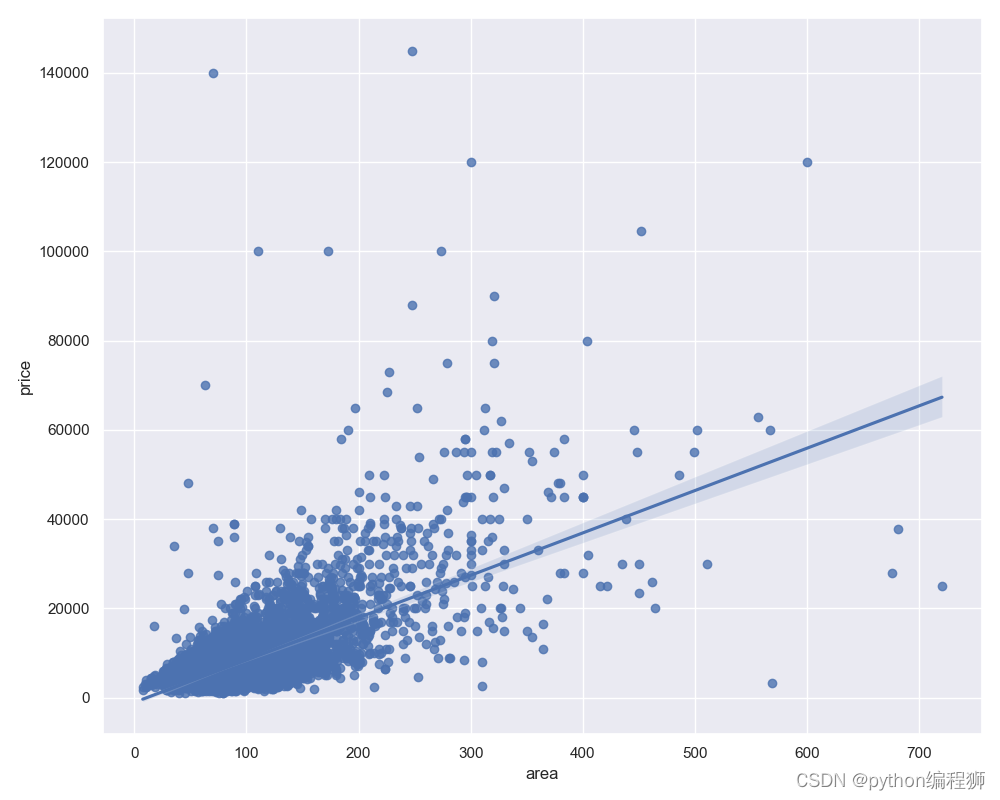
图6
如图5和5所示的分析结果。图5的纵坐标代表租房数量占比,横坐标代表租房面积区间。从图中可以发现,在所有的租房中,面积在50到150平米的租房数量远远高于其他面积的租房数量,而面积在300平米以上的租房的数量几乎为0。通过distplot和kdeplot绘制柱状图观察面积特征的分布情况,属于长尾型分布,这说明了有一些租房的面积很大,且超出正常范围的租房。通过regplot绘制了面积和房屋总价之间的散点图,发现面积与总价基本呈现线性关系,符合基本常识:面积越大,价格越高。但是图中也有例外的点:有的二手房面积超过了500平米,价格不到20000元;有的租房面积在100平米左右,但价格却在100000元左右。
楼层分析
楼层分析是基于租房的所在楼层,对不同楼层的租房进行统计作图,更能直观的看到不同楼层租房的数量。
绘制楼层分析图:使用seaborn库的countplot()函数绘制楼层数量统计图。
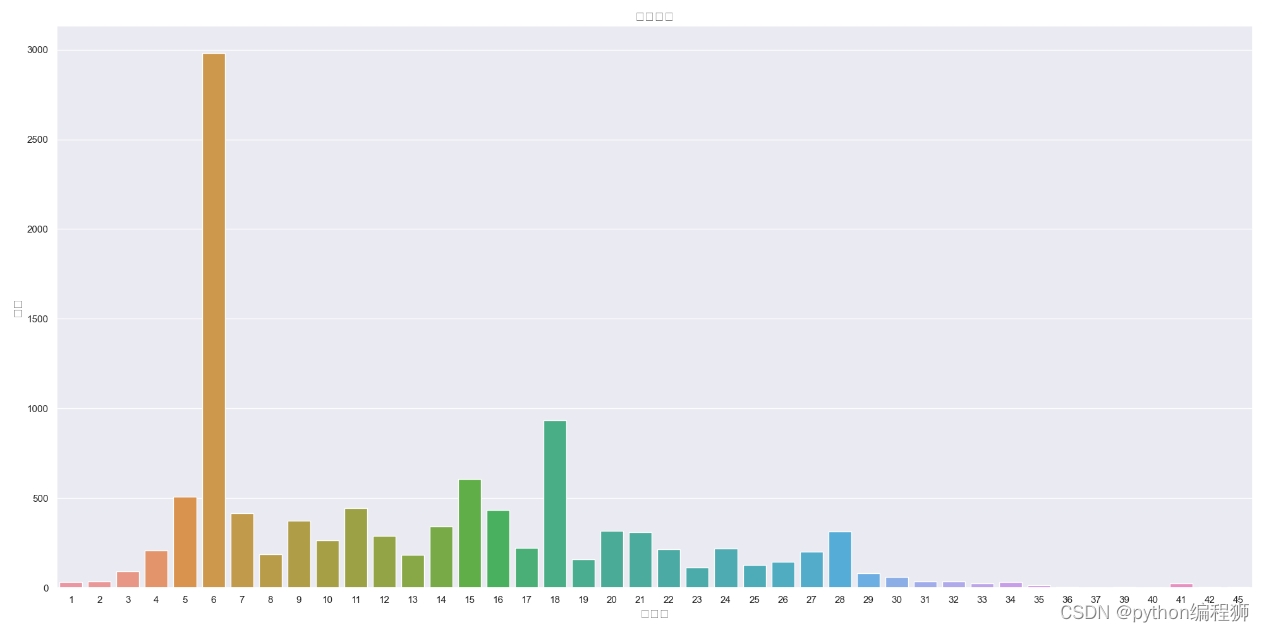
图7
如图7所示的分析结果。在中国的传统意识中,认为租房层数后的数字代表了深远的意义。从图中可以看到,6层、18层和28层二手房数量最多。但是单独的楼层特征没有什么意义,因为每个小区住房的总楼层数都不一样,我们需要知道楼层的相对意义。另外,楼层与文化也有很重要联系,比如中国文化七上八下,七层相对于8层的确是更受欢迎。当然,正常情况下中间楼层是比较受欢迎的,价格也高,底层和顶层受欢迎度较低,价格也相对较低。所以楼层是一个非常复杂的特征,对房价影响也比较大。
相关分析通过热力图,分析房价和哪些因素的关系比较密切,然后再试图利用数据挖掘方法,找出这些因素和房价之间的关系,从而实现利用这些关键因素对房源价格的预测。
绘制特征相关系数矩阵热图:使用seaborn库的heatmap()函数绘制特征相关系数矩阵的热图。
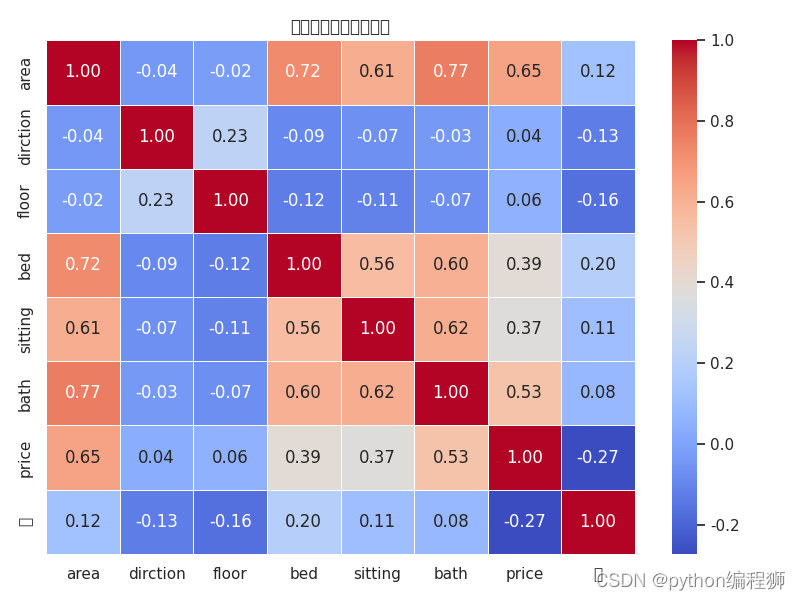
图8
图 8中左图中的数字构成了一个对称矩阵。以第二行第一列的-0.04为例,这代表朝向对面积的影响因子为0.04。其中,列表中的数字值越大,代表横纵坐标所代表的两个因素互相影响力越大。矩阵中对角线的数字都为1.00,观察横纵坐标,我们发现其横纵坐标代表的影响是一样的。可以看到,在房价的影响因素里,房屋面积和卧室数是主要的影响因素。
箱型图分析异常值
绘制特征箱线图:使用seaborn库的boxplot()函数绘制特征的箱线图。
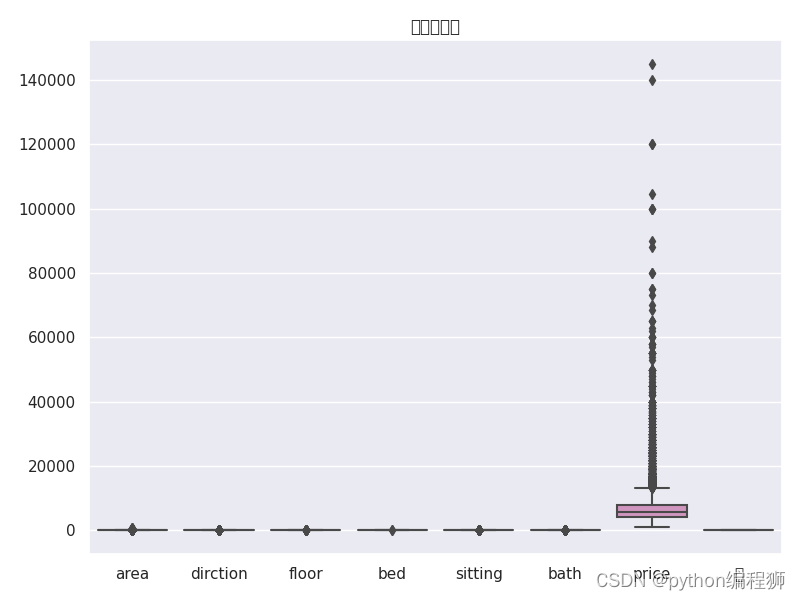
图9
由图9可知,价格列数据异常值很多,其他列的异常值几乎没有,所以要对价格列进行异常处理。
5. 异常值处理
删除异常值:根据设定的下限和上限阈值lower_threshold和upper_threshold,使用布尔索引对price列中的异常值进行删除。
6. 线性回归模型
单变量线性回归:
提取特征和标签:选择'area'作为特征,'price'作为标签。
创建线性回归模型:使用sklearn.linear_model库的LinearRegression()创建线性回归模型。
训练模型:使用fit()函数对数据进行训练。
预测结果:使用predict()函数对特征进行预测。
输出模型参数和评估指标:输出回归系数、截距和均方误差(MSE)、决定系数(R^2)。
7. 多变量线性回归模型
提取特征和标签:选择除'price'之外的其他特征作为输入,'price'作为标签。
创建多变量线性回归模型:使用sklearn.linear_model库的LinearRegression()创建多变量线性回归模型。
训练模型:使用fit()函数对数据进行训练。
预测结果:使用predict()函数对特征进行预测。
输出评估指标:输出均方误差(MSE)和决定系数(R^2)。
8. 随机森林回归模型
提取特征和标签:选择特征和标签。
划分训练集和测试集:使用train_test_split()函数划分数据集。
创建随机森林回归模型:使用sklearn.ensemble库的RandomForestRegressor()创建随机森林回归模型。
定义超参数空间:设定n_estimators、max_depth和min_samples_split的取值范围。
网格搜索寻找最优模型:使用GridSearchCV()函数进行网格搜索。
输出最优模型的评估指标:输出均方误差(MSE)和决定系数(R^2)。
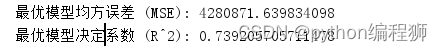
根据结果,可以得出以下结论:
线性回归模型:
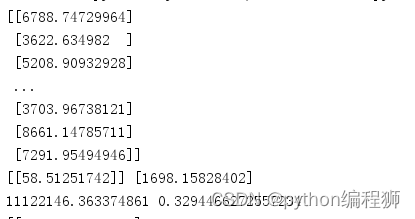
一元线性回归模型的预测结果显示,房屋面积对租房价格有显著影响,每增加1平方米的面积,租金约增加58.51元。
一元线性回归模型的均方误差(MSE)为11,122,146.36,决定系数(R^2)为0.33,说明该模型对租房价格的解释能力较低。
多元线性回归模型:
多元线性回归模型的预测结果显示,除了房屋面积外,其他特征变量(朝向、楼层、卧室数、客厅数、卫生间数、区域)也对租房价格有影响。
多元线性回归模型的均方误差(MSE)为6,971,547.48,决定系数(R^2)为0.58,相较于一元线性回归模型,多元模型的预测性能有所提升。
随机森林回归模型:
经过网格搜索寻找最优模型后,随机森林回归模型的最优配置是:决策树数量为100,最大深度为None,节点划分所需的最小样本数为2。
最优模型的均方误差(MSE)为4,280,871.64,决定系数(R^2)为0.74,说明随机森林回归模型对租房价格的解释能力较高。
通过模型比较和评估,可以发现随机森林回归模型在预测租房价格方面具有较好的性能,相较于一元线性回归和多元线性回归模型,其具有更低的均方误差和更高的决定系数,因此可视为最佳模型选择。








—— 如何在Ubuntu18.04中使用自己的单目摄像头运行ORB_SLAM3(亲测有效,踩坑记录))










和filter()函数?)