
麦克纳姆轮是一种常见的全向移动机构,可以使机器人在平面内任意方向平移,同时可以利用差速轮车的属性实现自转,能够在狭窄且复杂多变的环境中自由运行,因而被广泛应用于竞赛机器人和特殊工业机器人场景。



Ps:最新的BYD仰望U8也有一款是麦克纳母轮版本,但是由于运动的不稳定性和轮胎摩擦大等问题,始终不能大规模量产,B站有个up主特别搞笑,还可以用个管子去塞住仰望U8的麦克纳母轮间隙,想着开在路上这么多杂物还实在是难绷。而且由于他的运动学原理规定了他的移动速度不能过快,如果在崎岖不平的路面,可能会造成辊棒无法分解为横向和纵向两个分力,不能分解力就会造成侧移误差。而且麦轮在这种崎岖不平的路面存在较大的滚动摩擦,辊棒的磨损比汽车那种普通轮胎要更严重,继而带来的是使用成本的增加,所以麦轮只适用于低速场景和比较平滑的路面。即使满足路面平滑的要求了,汽车乘坐的舒适性也需要考虑,辊棒永远不会像轮胎那样始终与地面接触,这样就会造成颠簸震动。在实际的应用过程中我也发现,单纯靠开环位置控制和速度控制是无法实现麦轮移动机器人的精准控制的,需要添加姿态反馈和实时的位置反馈才能做到,这也是因为路面和轮子误差的问题,这也是他无法做到普及的原因。
特性和控制问题:
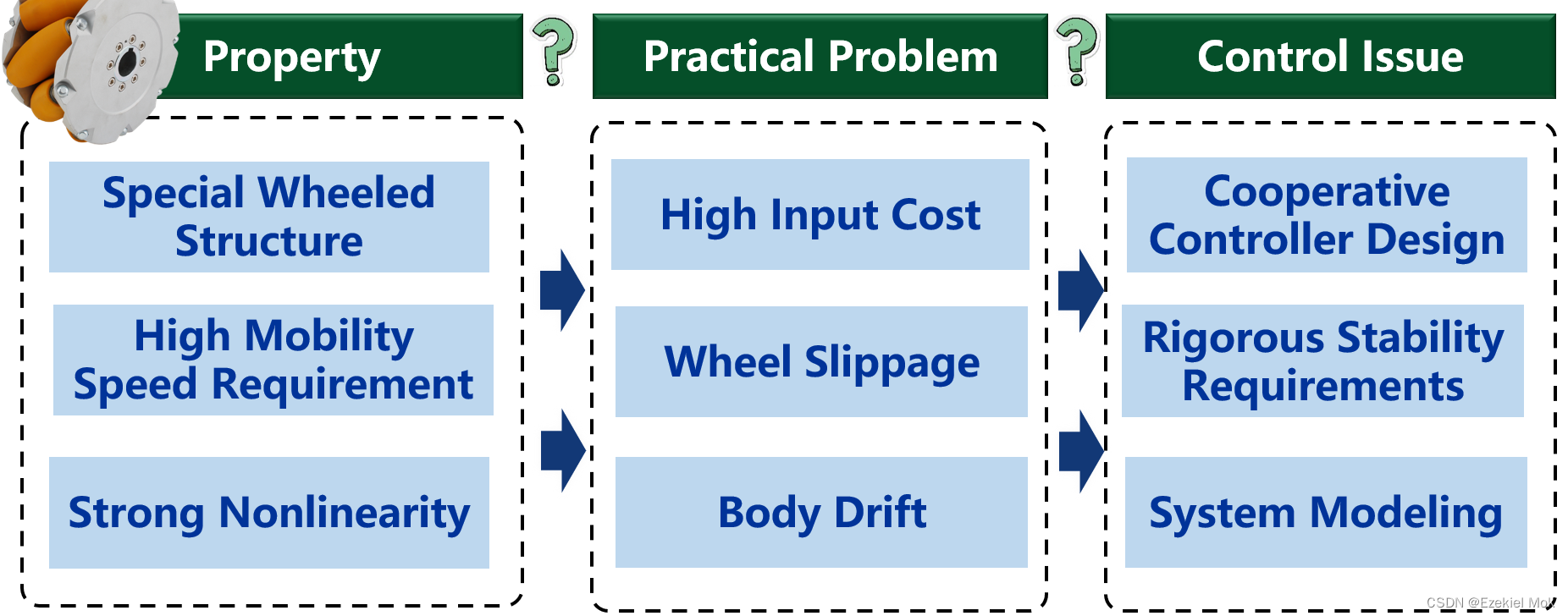
但是呢,在室内狭隘的环境,他能做到不完整约束机器人做不到的事情,例如自动旋转侧移去完成所需要的任务,为此,本文基于MATLAB Simulink的Simscape模块介绍一个麦轮移动机器人具体的控制建模过程,包含麦轮的建模,运动学和动力学模型,simscape导入搭建、力接触配置、位置环和转速环PID控制策略。

1. 麦克纳母轮移动机器人运动学和动力学建模
1.1 运动学方程
运动学模型(可以参考论文或者古月居的文章,都有建模)是为了构建起电机驱动角度坐标系、机器人坐标系和大地坐标系三者之间的实时相互映射关系。
以单个轮子为例:

当单独考虑四个轮子时:


因此,正运动学方程如下:

逆运动学方程:


1.2 动力学方程
目前有两种方式构建动力学,一种是利用轮子的受力构建起牛顿力学方程,第二种事利用欧拉拉格朗日构建起能量的守恒方程。
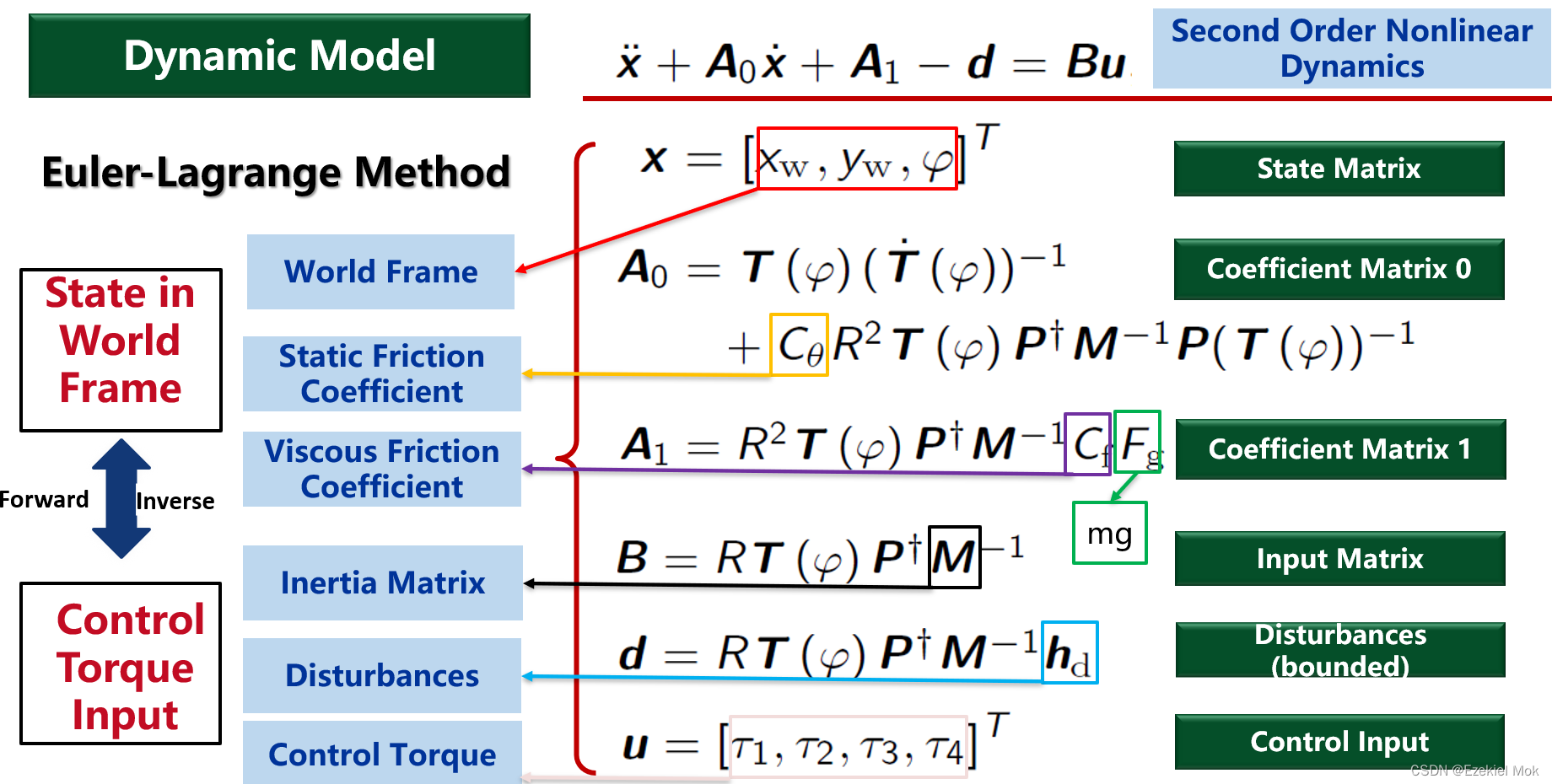
2. 麦克纳母轮移动机器人Simulink/Simscape模型建立
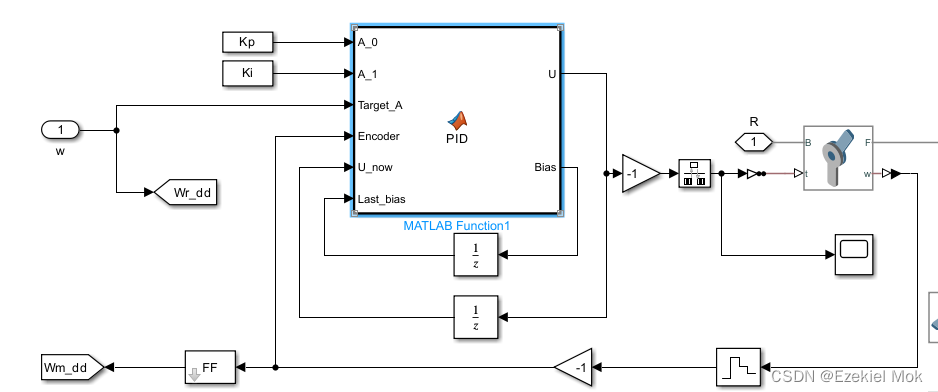
2.1. 单个麦克娜姆轮车的控制回路
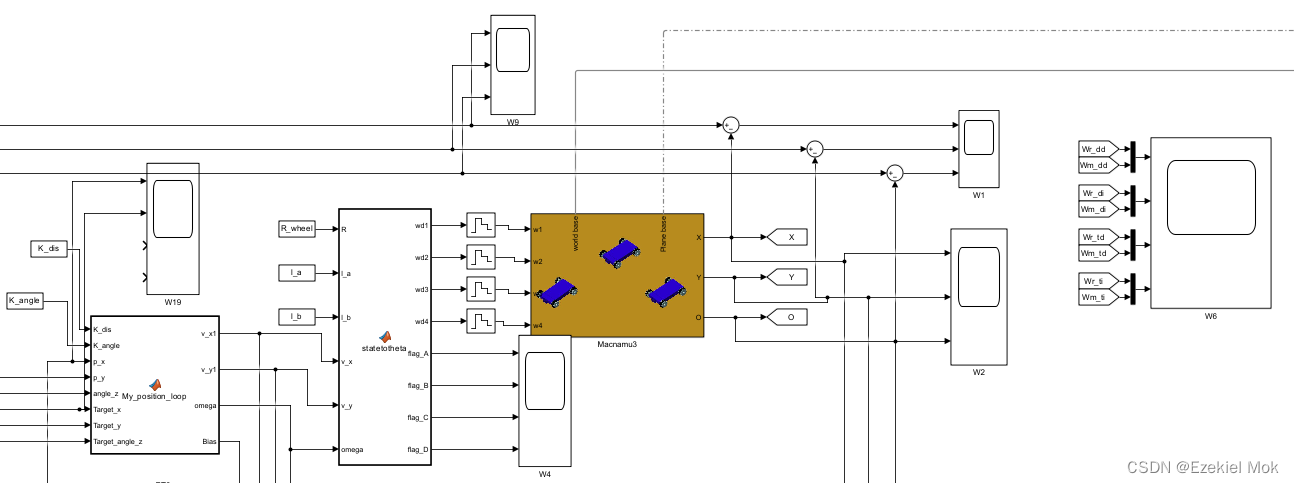

2.2. 底盘到轮子法兰的变换关系

2.3 传感器配置
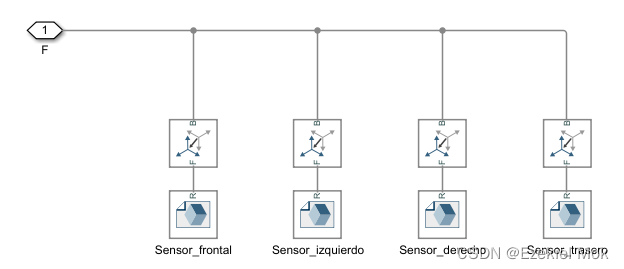
2.4. 单个轮子的接触力配置
 2.5. 空间位置和姿态环PID
2.5. 空间位置和姿态环PID
function [v_x1, v_y1, omega, Bias] = My_position_loop(K_dis, K_angle, p_x, p_y, angle_z, Target_x, Target_y, Target_angle_z)
v_x1 =0;
v_y1 =0;
delta_x = Target_x-p_x;
delta_y = Target_y-p_y;
DIF_x = delta_x * cos(angle_z) - delta_y * sin(angle_z);
DIF_y = delta_x * sin(angle_z) + delta_y * cos(angle_z);
DIF_anglez= Target_angle_z - angle_z;
Bias = sqrt(DIF_x^2 + DIF_y^2);
Target_V = K_dis * Bias;
angle = atan2(abs(DIF_y), abs(DIF_x));
if Bias > 0.2temp_x = Target_V * cos(angle);temp_y = Target_V * sin(angle);omega = K_angle * (DIF_anglez);if DIF_x >=0 && DIF_y >=0v_x1 = temp_x;v_y1 = temp_y;elseif DIF_x >=0 && DIF_y < 0v_x1 = temp_x;v_y1 = -temp_y;elseif DIF_x <0 && DIF_y < 0v_x1 = -temp_x;v_y1 = -temp_y;elseif DIF_x <0 && DIF_y >= 0v_x1 = -temp_x;v_y1 = temp_y;end
elsev_x1 = 0;v_y1 = 0;omega = K_angle * (DIF_anglez);
end
end2.5. 运动学速度映射
function [wd1, wd2, wd3, wd4, flag_A, flag_B, flag_C, flag_D] = statetotheta(R, l_a, l_b, v_x, v_y, omega)
robot_state = zeros(3, 1);
J =[1, 1, (l_a + l_b);1, -1, -(l_a + l_b);1, -1, (l_a + l_b);1, 1, -(l_a + l_b)];
robot_state(1) = v_x;
robot_state(2) = v_y;
robot_state(3) = omega;
theta = (1 / R) * J * robot_state;
wd1 = theta(1);
wd2 = theta(2);
wd3 = theta(3);
wd4 = theta(4);
if wd1 >= 0flag_A=1;
elseflag_A=-1;
end
if wd2 >= 0flag_B=1;
elseflag_B=-1;
end
if wd3 >= 0flag_C=1;
elseflag_C=-1;
end
if wd4 >= 0flag_D=1;
elseflag_D=-1;
end
end
3. 电机增量式PID控制器设计
function [U, Bias] = PID(A_0, A_1, Target_A, Encoder, U_now,Last_bias)
Bias = Target_A - Encoder;
U = U_now + A_0*(Bias - Last_bias) + A_1 * Bias;
end
3. 模型和参数配置
包括机身的尺寸,摩擦系数,PID增益,滤波器模型,状态初值等等。
A=[1,-1.778631777824585,0.800802646665708];
B=[0.005542717210281,0.011085434420561,0.005542717210281];
l_a=(0.15);
l_b=(0.108+0.032);
l_wheel=0.108;
R_wheel=0.05;
dc=1.000000000000000e-05;
dcr=1.000000000000000e-03;
df=0.3;
dm=1000;
Ki=0.002;
Kp=0.08;
K_dis = 0.095;
K_angle = 0.45;
sf=0.50;
st=1000000;
T=0.01;
numFF=[0.00554271721028068,0.0110854344205614,0.00554271721028068];
denFF=[1,-1.77863177782459,0.800802646665708];
FF=tf(numFF,denFF);
FF.Ts=T;
Ki_angle=1;
Kp_angle=1;
x2_0 = -0.8;
y2_0 = pi+0.8;
z2_0 = 0.05;
x1_0 = -0.8;
y1_0 = -0.8+pi;
z1_0 = 0.05;
x_0 = 0;
y_0 = pi;
z_0 = 0.05;
offset_x1 = -0.8;
offset_x2 = -0.8;
offset_y1 = 0.8;
offset_y2 = -0.8;4. 仿真效果
4.1. 轨迹曲线
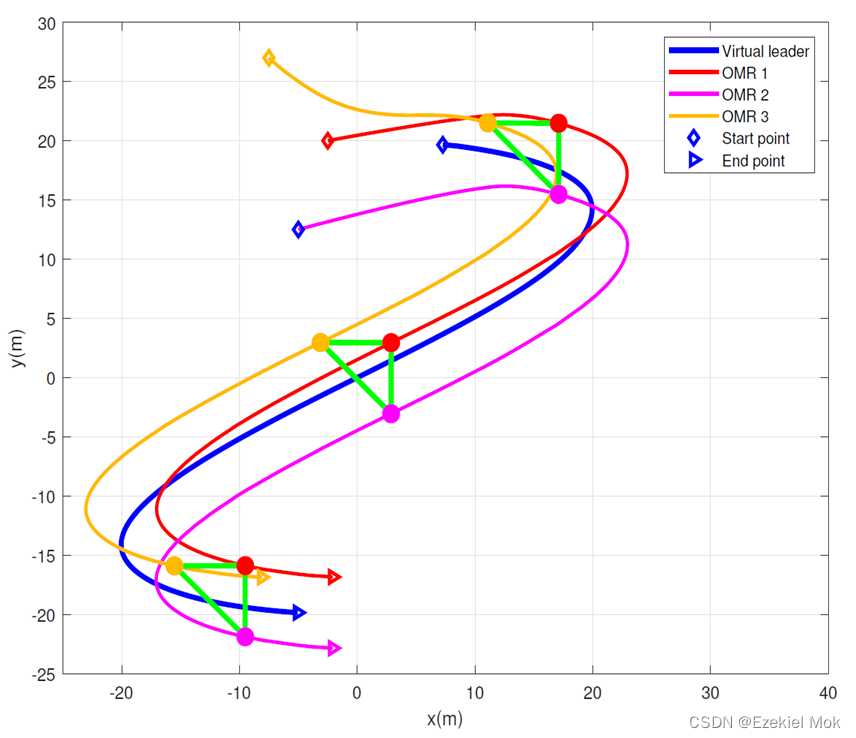
4.2. 其中一个电机的期望和实际跟踪曲线

4.3. 空间状态期望和实际跟踪曲线

4.3. Simscape实际仿真效果

5. 实验效果
该实验也是硕士时候和好哥们合作做的,仅供参考,任务不一样,但是核心算法都是编队规划和PID控制。




—ConfigurationClassPostProcessor —— 后续处理)





)









